[Leetcode] 605. Can Place Flowers

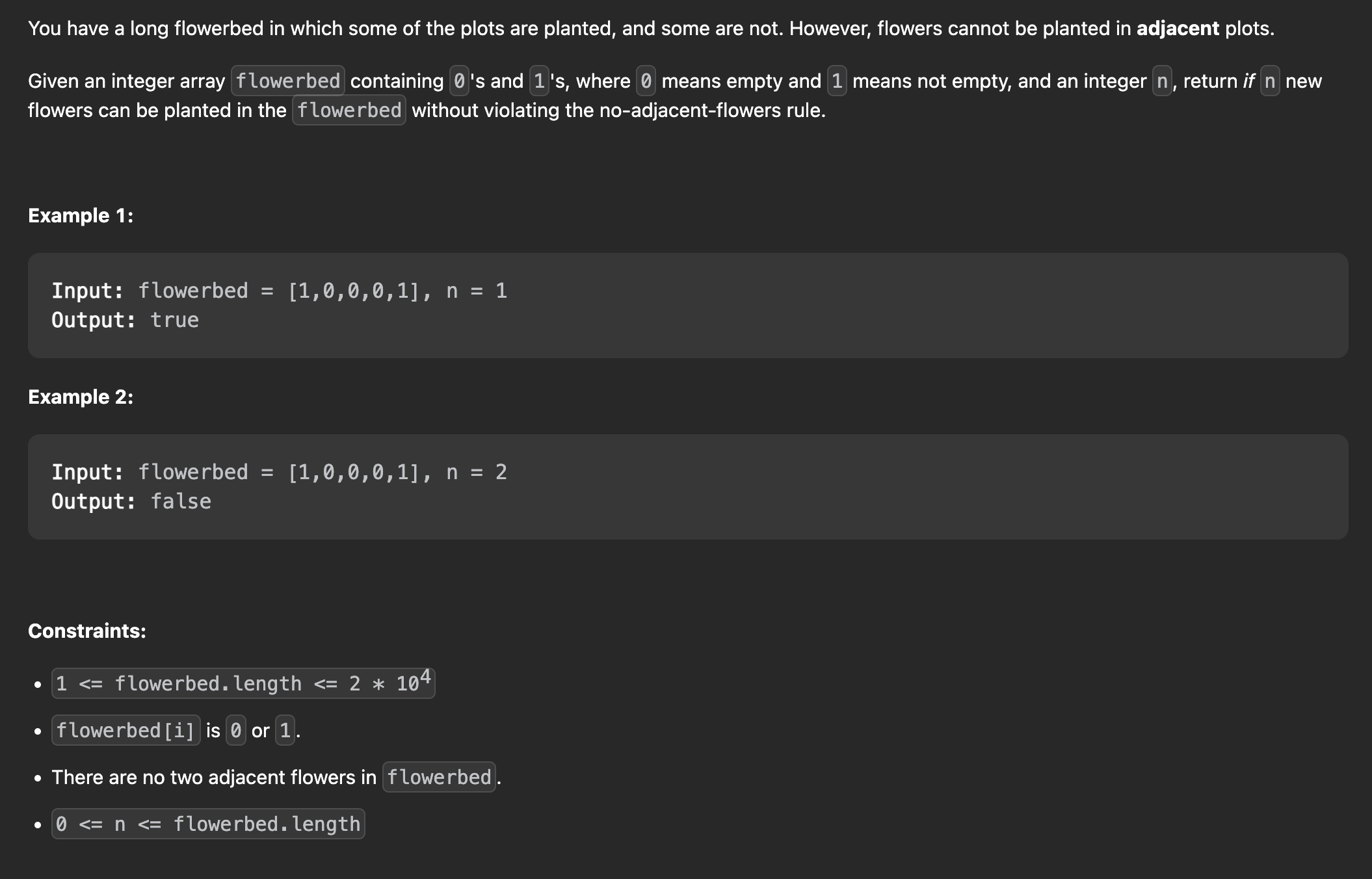
문제

나의 풀이 & 다른 풀이

• index i를 중간에 두고 i-1/i/i+1가 모두 0인 경우를 찾아 카운트했다.
• 첫 시도에 실패가 떠서 뭘 잘못했을까.. 봤는데 생각하지 못한 경우의 수가 있었다.

위와 같이 flowerbed가 주어진 경우, 기존 내 코드로는 2번의 경우 밖에 카운트하지 못 하고 있었다.
원래 내가 쓴 코드는 시간복잡도를 낮추기 위해 000/010/001/100/101/100 경우를 거의 모두 나눠서 i++; i+=2; i+=3;을 각 경우에 맞게 수행해줬는데, 여기서 위 경우의 수를 같이 담으려고 하니 머리가 터질 것 같았다 ^^;

여러가지 시도해보다가 결국 시간이 1시간을 초과해 풀이를 봤다.

public class Solution {
    public boolean canPlaceFlowers(int[] flowerbed, int n) {
        int cnt = 0;
        for(int i = 0; i < flowerbed.length && cnt < n; i++) {
            if(flowerbed[i] == 0) {
               int next = (i == flowerbed.length - 1) ? 0 : flowerbed[i + 1];  
               int prev = (i == 0) ? 0 : flowerbed[i - 1]; 
               if(next == 0 && prev == 0) {
                   flowerbed[i] = 1;
                   cnt++;
               }
            }
        }
        
        return cnt == n;
    }
}

• 여기서 포인트는
  int next = (i == flowerbed.length - 1) ? 0 : flowerbed[i + 1];
int prev = (i == 0) ? 0 : flowerbed[i - 1];
  이 두 구문인 듯하다.

• 또한 n=0으로 들어오는 경우도 cnt<n을 통해 처리해주어야 한다.

후기

혼자 힘으로 끝까지 풀어내지 못 해서 아쉬움이 남는 문제다.
하지만 이 문제처럼 no-adjacent-rule을 가진 문제를 다음에 만나게 된다면, 맨 앞과 맨 뒤의 경우를 반드시 함께 고려해보아야겠다는 통찰을 얻을 수 있었다.