문제 바로가기

문제

풀이

첫번째 풀이

접근 방법

1. x보다 큰 수를 차례대로 방문한다.
2. x와의 비트 차이를 계산한다.

• xor 연산자를 통해 두 숫자 중 다른 비트를 골라내고, 모든 비트(64)를 검사하여 다른 비트의 수를 찾는다.

3. 차이가 1~2개일 때까지 계속한다.

코드

class Solution {
    public long[] solution(long[] numbers) {
        long[] answer = new long[numbers.length];
        for(int i=0; i<numbers.length; i++) {
            answer[i] = func(numbers[i]);
        }
        return answer;
    }
    
    public long func(long x) {
        long result = x+1;
        while(!checkBitDifference(x,result)) {
            result ++;
        }
        return result;
    }
    
    public boolean checkBitDifference(long a, long b) {
        boolean result = true;
        int cnt = 0;
        long xor = a ^ b;
        for(int i=0; i<64; i++) {
            if((xor & (1l<<i)) != 0) cnt++;
            if(cnt > 2) {
                result = false;
                break;
            }
        }
        
        return result;
    }
}

이 코드를 제출하니 테스트케이스 10번과 11번에서 시간초과가 떴다.

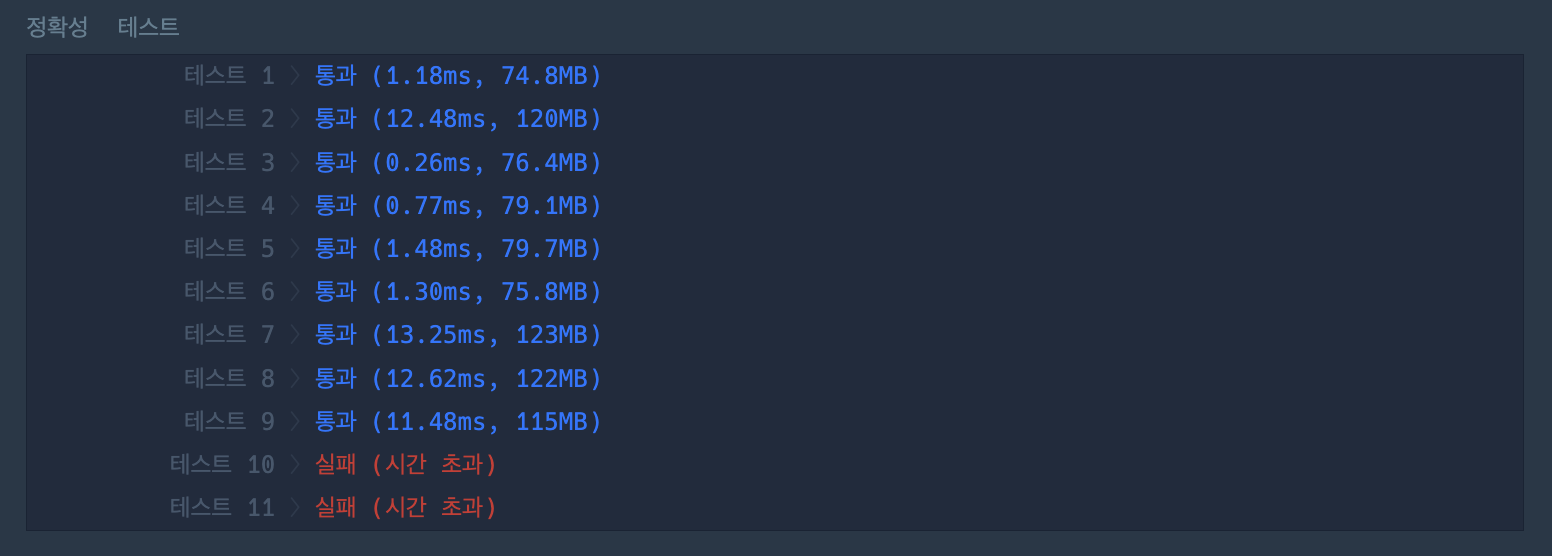
예상하기로는 엄청 큰 수가 주어졌을 때, 모든 비트에 대해 checkBitDifference() 메서드를 실행하는 데에서 시간이 오래 걸리는 것 같다.

따라서 result ++; 를 하여 x보다 큰 수를 차례대로 방문하는 것이 아닌, 다른 방법이 필요하다.

정답 풀이

이 문제는 각 숫자에 대해서 직접 f(x)를 계산해보고, 그 수를 이진수로 변환하여 비트를 보면서 규칙을 찾아내야 하는 문제였다.

이 게시글의 설명을 보고 규칙을 이해하였고, 코드를 다시 짰다.

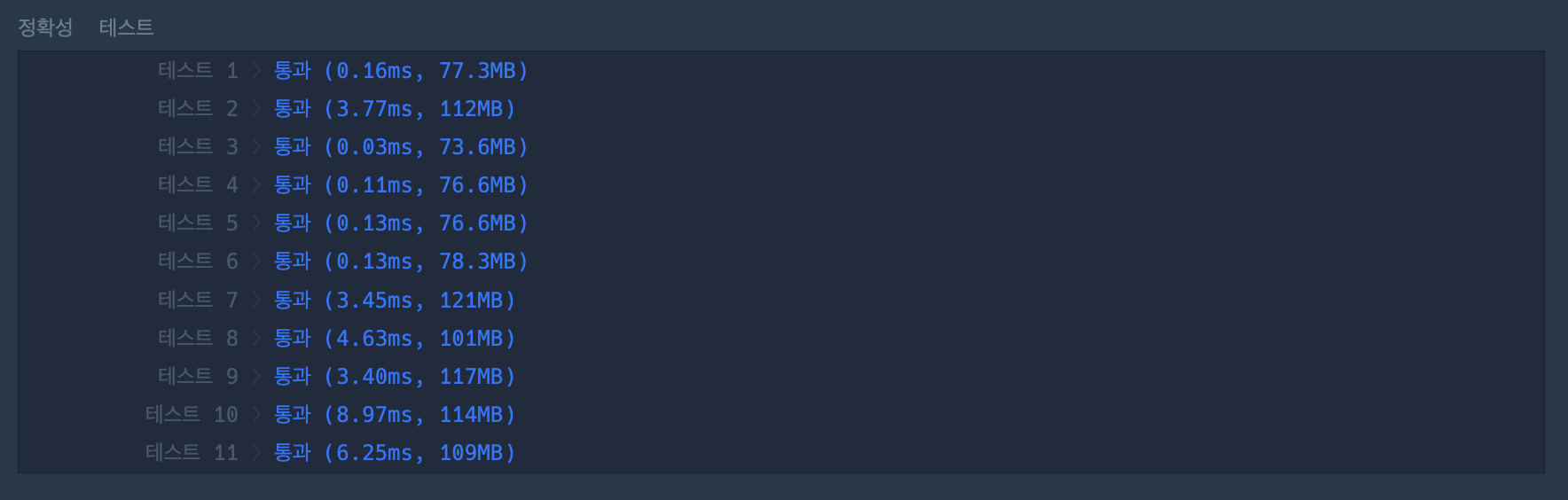
최종 제출 코드

class Solution {
    public long[] solution(long[] numbers) {
        long[] answer = new long[numbers.length];
        for(int i=0; i<numbers.length; i++) {
            answer[i] = func(numbers[i]);
        }
        return answer;
    }
    
    public long func(long x) {
        long result = x;
        // 가장 오른쪽 비트에서부터 시작해서
        for(long i=1;; i=(i<<1)) {
            if((result & i) == 0) { // x의 비트가 0이면
                result = (result | i); // 해당 위치의 0을 1로 바꿔주고
                result = (result ^ (i>>1)); // 이전 비트를 1에서 0으로 바꿔준다.
                break;
            }
        }
        return result;
    }
    
}

---

흠 ... 규칙 찾아내는 문제가 제일 싫다 ...
그래도 오랜만에 비트 연산을 활용하는 문제를 푼 것에 의의를 두어야겠다.