[프로그래머스] Lv.2 k진수에서 소수 개수 구하기 (Java)

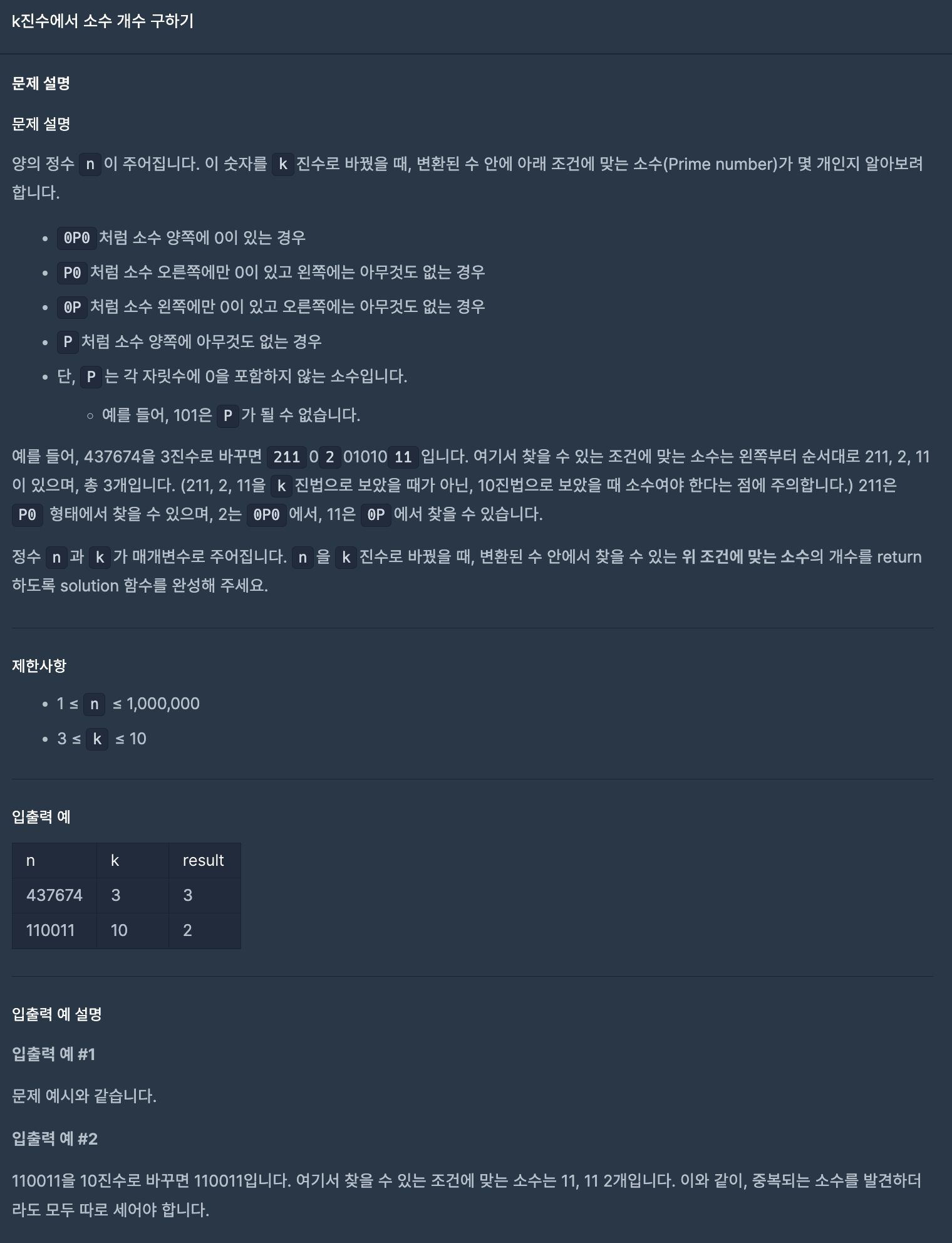
문제

풀이1

• k진수로 변환하여 String kStr에 넣는다.
• 0을 기준으로 split하여 String[] numbers에 담는다.
• numbers의 요소를 하나씩 검사하며 소수인지 판별한다. 소수일 시 정답에 카운트한다.
  -1은 소수가 아니므로 카운트하지 않는다.
  
• isPrime(int x): x가 소수인지 판별하는 메서드

class Solution {
    public int solution(int n, int k) {
        String kStr="";
        int remained=0;
        while(n>0) {
            remained = n%k;
            kStr = remained+kStr;
            n/=k;
        }
        
        String[] numbers = kStr.split("0");
        int answer = 0;
        for(int i=0;i<numbers.length;i++) {
            if(numbers[i].equals("1") || numbers[i].equals("")) continue;
            if(isPrime(Integer.parseInt(numbers[i]))) answer++;
        }
              
        return answer;
    }
    
    boolean isPrime(int x) {
        for(int i=2;i*i<=x;i++) {
            if(x%i==0) return false;
        }
        
        return true;
    }
}

풀이2

class Solution {
    public int solution(int n, int k) {
        String kStr="";
        int remained=0;
        while(n>0) {
            remained = n%k;
            kStr = remained+kStr;
            n/=k;
        }
        
        String[] numbers = kStr.split("0+");
        int answer = 0;
        for(int i=0;i<numbers.length;i++) {
            if(numbers[i].equals("1")) continue;
            if(isPrime(Long.parseLong(numbers[i]))) answer++;
        }
              
        return answer;
    }
    
    boolean isPrime(long x) {
        for(int i=2;i*i<=x;i++) {
            if(x%i==0) return false;
        }
        
        return true;
    }
}

바뀐 점은

• split()의 regex에 "0" 대신 "0+"를 넣었다.
• k진수로 변환한 숫자인 numbers[i]를 int가 아닌 long에 담는다.
• n의 범위는 1 ≤ n ≤ 1,000,000 이므로 이를 k진수로 변환할 시 int의 범위를 넘을 수 있다.

제발 범위를 항상 생각하자 !!!!!

헌데 이렇게 바꾸어도 계속해서 테스트케이스 1번이 시간초과가 났다.
뭐가 문젤까 생각하다가 통과한 다른 사람들의 코드를 보아도 내 코드와 별반 다를 게 없었다.
다른 점은 소수 판별 시 제곱근까지 확인할 때, 나는 i*i<=x로 계산했지만 다른 사람들은 Math.sqrt()를 사용한 정도..?

혹시나 해서 내 코드도 Math.sqrt를 사용하도록 바꿨더니, 바로 테스트케이스 1번에도 통과했다.
-> 찾아봐도 정확한 이유는 모르겠다. 다만 직접 i*i를 곱하는 연산이 sqrt 메서드에서 행하는 연산보다 시간이 오래걸리나보다 .. 싶다.

Math.sqrt() 사용 코드

    boolean isPrime(long x) {
        for(int i=2;i<=(int)Math.sqrt(x);i++) {
            if(x%i==0) return false;
        }
        
        return true;
    }