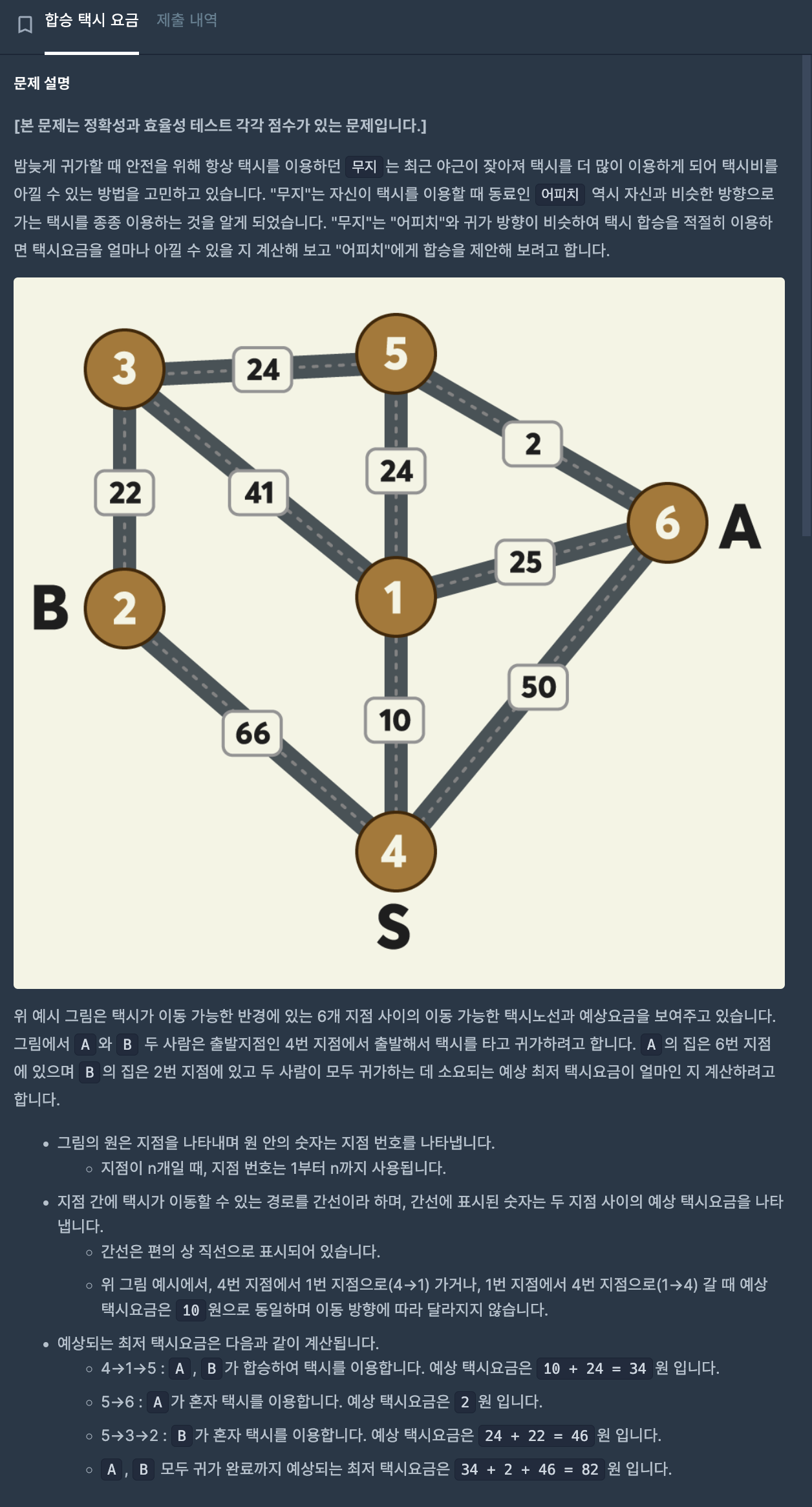
문제

문제 바로가기

풀이

일단 최단 거리를 구하는 문제이고, 출발지 S, 도착지 A, 도착지 B가 있다.
따라서 S -> A의 경로, S -> B의 경로를 모두 구해야 한다.

그런데 두 사람이 출발지 S에서 동시에 출발해서 어떤 경유지 V까지는 함께 갈 수 있다. 그리고 이 V에서 다시 도착지 A와 도착지 B 각각으로 도착하는 거리를 구해야 하는 것이다.

따라서 구해야 하는 정보는 다음과 같다.

1. S -> V 최단 경로
2. V -> A 최단 경로
3. V -> B 최단 경로

그리고 모든 노드 V에 대해 이 세 경로의 합이 최소가 되는 경우를 찾아서 반환하면 된다!

경유지 V는 모든 노드가 될 수 있다. (n개의 노드가 모두 경유지가 될 수 있음)
따라서 결국 S, A, B 세 노드를 각각 시작점으로 하는 다익스트라 알고리즘을 세 번 돌려서 모든 노드에 대한 해당 노드로의 최단 거리를 구한다.

현재 문제 상황은 비방향성 그래프이기 때문에 다른 모든 노드로부터(from) A, B로(to)의 최단 거리를 구하는 다익스트라 알고리즘에서 기존 리스트를 사용할 수 있다.
만일 방향성 그래프 상황이었다면 reverseList를 구성하여서 A,B를 시작점으로 하는 다익스트라 알고리즘을 수행하여야 한다.

구현 코드

import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;

public class Solution {
  static ArrayList<ArrayList<Path>> pathList;
  static int N; // vertex 개수
    
  static class Path implements Comparable<Path>{
    int to;
    int cost;
    public Path(int to, int cost) {
      this.to = to;
      this.cost = cost;
    }
    @Override
    public int compareTo(Path p) {
      return this.cost - p.cost;
    }
  }
    
  public int solution(int n, int s, int a, int b, int[][] fares) {
    // n : 지점 갯수, s : 출발 지점, a : a의 도착 지점, b: b의 도착 지점
    N = n;
    pathList = new ArrayList<>();
    for(int i=0; i<=n; i++) {
      pathList.add(new ArrayList<>());
    }
    for(int i=0; i<fares.length; i++) {
      pathList.get(fares[i][0]).add(new Path(fares[i][1], fares[i][2]));
      pathList.get(fares[i][1]).add(new Path(fares[i][0], fares[i][2]));
    }
    int[] together = dijkstra(s);
    int[] toA = dijkstra(a);
    int[] toB = dijkstra(b);

    int min = Integer.MAX_VALUE;
    for(int i=1; i<=n; i++) {
      int totalCost = together[i] + toA[i] + toB[i];
      if(min > totalCost) {
        min = totalCost;
      }
    }
    return min;
  }

  public int[] dijkstra(int start) {
    int[] dist = new int[N+1];
    Arrays.fill(dist, Integer.MAX_VALUE);
    dist[start] = 0;
      
    PriorityQueue<Path> pq = new PriorityQueue<>();
    pq.add(new Path(start, 0));
      
    while(!pq.isEmpty()) {
      Path currentPath = pq.poll();
      int currentNode =  currentPath.to;
      for(Path path : pathList.get(currentPath.to)) {
        if(dist[path.to] > dist[currentNode] + path.cost) {
          dist[path.to] = dist[currentNode] + path.cost;
          pq.add(new Path(path.to, dist[path.to]));
        }
      }
    }
    return dist;
  }
}

---

뿌덧