다익스트라, 어떻게 하면 코드를 깔끔하게 작성할 수 있을까?
아이디어
아래의 흐름대로 떠올렸다.
먼저 대략적으로 원하는 결과와 흐름을 구상하고, 이후에 세부적인 구현 방법을 떠올리는 편이다.
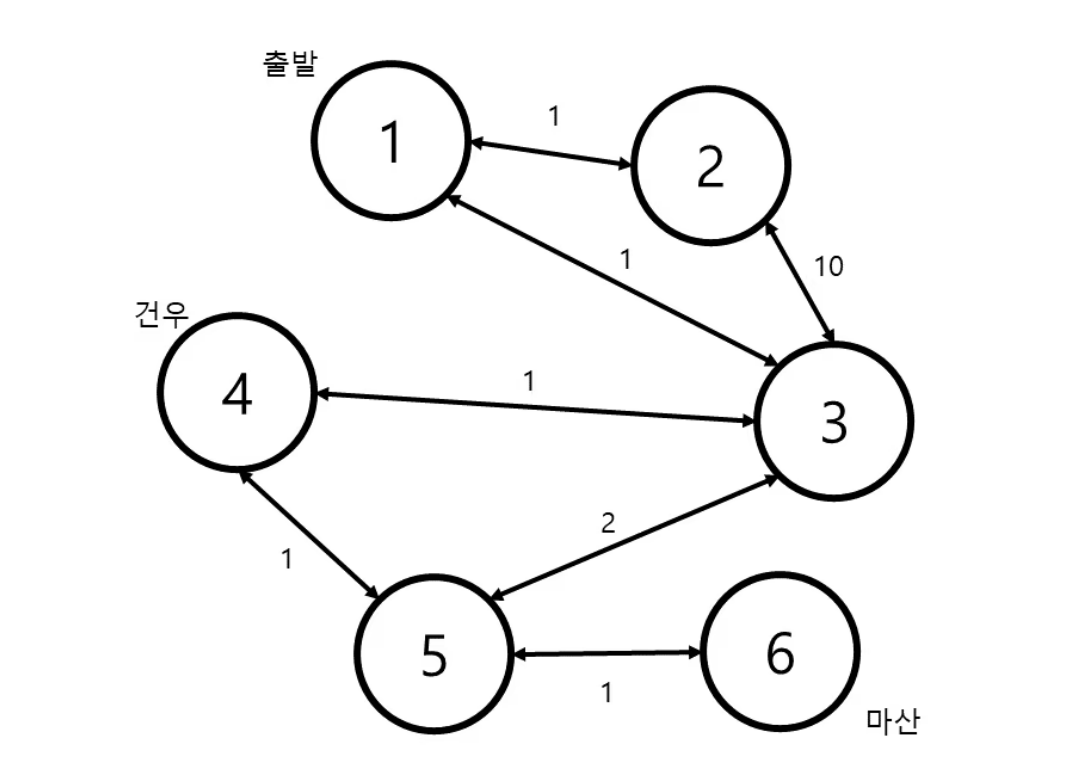
민준이가 마산까지 가는 데 필요한 최단 거리
시작 정점(u) 에서 다른 정점들(v)까지 최단 거리를 구한다.
그 최단 거리를 담을 long[] diff의 결과는 다음과 같을 것이다.
diff = [-1, 0, 1, 1, 2, 3, 4](인덱스 0은 노드 번호를 맞추기 위해 설정된 값으로, 인덱스 1부터 살피면 된다.)
그러면 출발점(1번)에서 도착점(6번)까지 최단 거리는 diff[6]인 4가 된다.
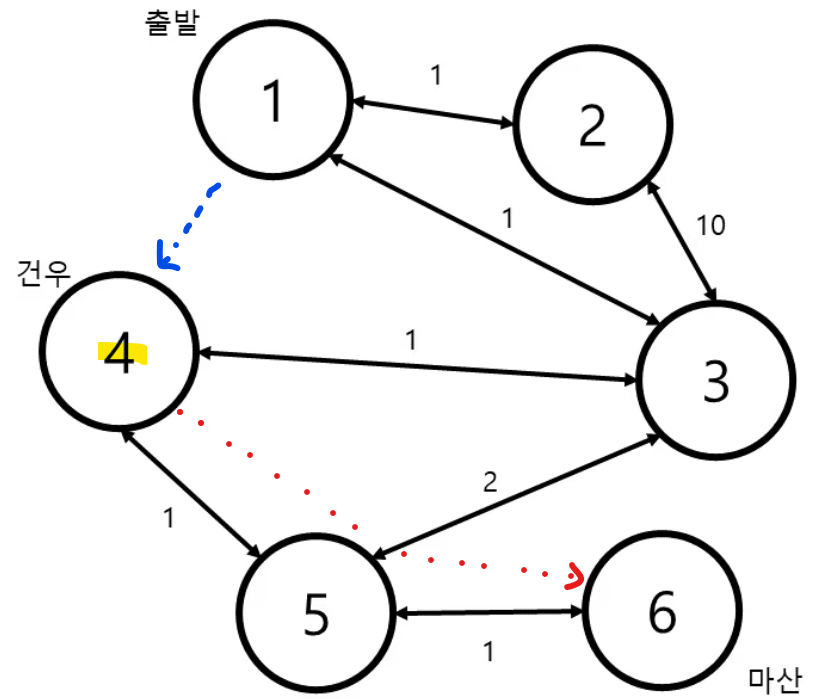
건우를 거치는 최단 거리
출발점부터 건우(P)까지, 건우(P)부터 도착점까지 각 최단 거리의 합이 총 건우를 거쳐서 가는 최단 거리가 된다.
출발점부터 건우까지 최단거리 = diff[P]건우부터 도착점까지 최단 거리를 구하는 방법은 민준이가 마산으로 갈 때 구한 방법과 동일하다.
건우를 시작 정점으로 하여 다른 정점들까지 최단 거리를 구하는 것이다.
그러면 건우에서 시작하는 최단 거리 배열은 다음과 같을 것이다.
diff2 = [-1, 2, 3, 1, 0, 1, 2]각 정점까지 최단 거리를 구하는 방법
- 현재 정점에 인접한 정점들을 큐에 담는다.
- 큐에서 가장 edge값이 작은 것을 꺼내고, 최단 거리를 계산한다.
- 최단 거리 = min( diff[현재 정점], diff[이전 정점] + 이전 정점에서 현재 정점으로 오는데 필요한 edge값 )
- 위 과정을 모든 edge를 다 살펴볼 때 까지 반복한다.
정답 코드
public class Main {
static final long INF = -1;
static int V, E, P;
static long[] diff1; // 출발점: 민준
static long[] diff2; // 출발점: 건우
static int[][] graph;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
V = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
P = Integer.parseInt(st.nextToken());
graph = new int[V+1][V+1];
for(int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
graph[a][b] = c;
graph[b][a] = c;
}
diff1 = new long[V+1];
diff2 = new long[V+1];
Arrays.fill(diff1, INF);
Arrays.fill(diff2, INF);
diff1[1] = 0;
diff2[P] = 0;
// 시작 정점부터 각 정점까지 최단 거리
if(P == 1) {
System.out.print("SAVE HIM");
br.close();
return;
}
findDiff(1);
findDiff(P);
if(diff1[V] == diff1[P]+diff2[V]) {
System.out.print("SAVE HIM");
} else {
System.out.print("GOOD BYE");
}
br.close();
}
private static void findDiff(int start) {
boolean[][] visit = new boolean[V+1][V+1];
PriorityQueue<int[]> q = new PriorityQueue<>((int[] a, int[] b) -> a[2]-b[2]);//from,to,거리
q.offer(new int[] {start, start, 0});
while(!q.isEmpty()) {
int[] node = q.poll();
int u = node[0];
int v = node[1];
int e = node[2];
// 최단 거리 갱신
if(start == 1)
diff1[v] = (diff1[v] == -1) ? diff1[u]+e : Math.min(diff1[v], diff1[u]+e);
else
diff2[v] = (diff2[v] == -1) ? diff2[u]+e : Math.min(diff2[v], diff2[u]+e);
// 가능한 점점 찾기
for(int j = 1; j < V+1; j++) {
if(graph[v][j] > 0 && !visit[v][j]) {
q.offer(new int[] {v, j, graph[v][j]});
visit[v][j] = true; // 해당 간선 다시 이용 불가능
visit[j][v] = true;
}
}
}
}
}기타 고려사항
- diff는 누적합이 되기 때문에 int가 아닌 long 타입으로 설정했다.
- 큐에서 가장 짧은 간선을 꺼내기 때문에 우선순위 큐를 이용했다.
- 큐에 담기는 객체는 간선 정보다. 간선 비중과 함께 해당 간선이 어디서 어디로 가는건지 두 정점도 함께 저장한다.
{From정점, To정점, 간선 비중}이 모든 정보가 있어야 최단 거리를 구할 수 있다. - visit을 통해서 이미 확인한 간선을 다시 큐에 담지 않도록 처리했다.
- 민준이와 건우가 같은 위치(1)인 경우는 구출 가능으로 바로 답이 반환하였다. 이 부분을 먼저 처리하지 않으면 diff1과 diff2를 갱신시킬 때 조건문으로 인해 diff2가 구해지지 않는 문제가 생긴다.
self 피드백
큐에 어떤 정보를 담아야 하는지 좀 더 빠르게 파악할 필요가 있었다.