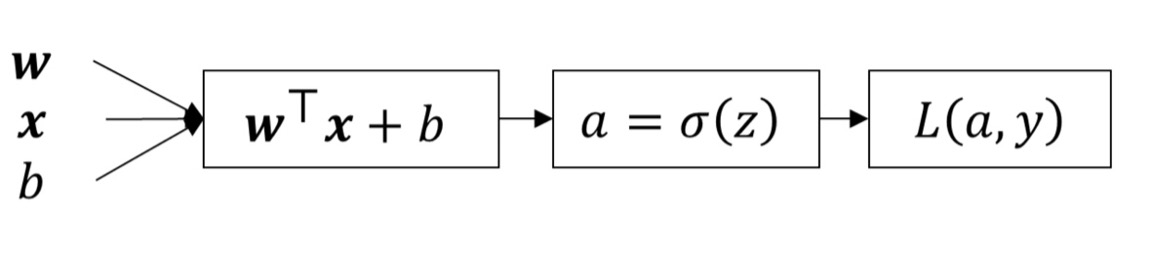Logistic Regression

sue991·2021년 3월 23일
딥러닝로지스틱 회귀
0

Deep Learning

목록 보기
1/1

용어

  • binary classification (이진분류) : 집합의 요소를 두 그룹으로 분류하는 것

    고양이이다 : Yes or No

Model

model은 architecture와 parameters로 이루어져 있다.

로지스틱 회귀란

예를 들어 사람의 나이와 당뇨병 발생 여부(정상 : 1, 발병 : 0)이 주어졌다고 생각해보자. 이를 회귀 모델을 구축하고 그래프를 그려보면,

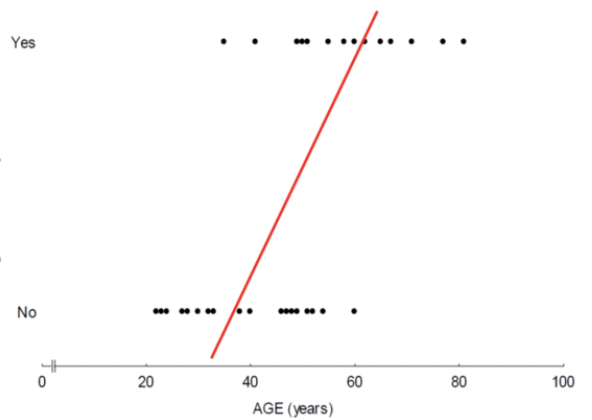
graph

이런 이상한 모양의 그래프가 나올것이다.

이는 주어진 변수가 범주형(categorical) 변수일 때, 즉 숫자가 의미가 있지 않을 때 다중선형회귀 모델을 사용한 것으로써 나타난 문제이다. 따라서 이러한 문제를 해결하기 위해 로지스틱 회귀 모델이 제안되었다.

로지스틱 회귀(Logistic Regression)는 회귀를 사용하여 데이터가 어떤 범주에 속할 확률을 0에서 1 사이의 값으로 예측하고 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류해주는 지도 학습 알고리즘이다.

Logistic Function

로지스틱 함수(logistic function)는 sigmoid function이라고도 불린다.

주어진 training Data (x,y)가 있을 때,

x∈Rnx \in R^n : input x는 그 어떤 real number도 받을 수 있지만

y∈0,1y ∈ {0,1} : output y는 항상 0에서 1사이의 값이 된다.

그래프로 보면 다음과 같다.

시그모이드 함수는 다음과 같다.

σ(x)=11+e−x\sigma(x) = \frac {1} {1+e^{-x}}

σ(+∞)=1\sigma(+\infin) = 1
σ(−∞)=0\sigma(-\infin) = 0

이처럼 xx가 무슨 값이 들어와도 y는 [0,1] 사이에 존재하게 된다.

Logistic Regression은 x∈Rnx \in R^n 가 주어졌을 때,
y^=P(y=1∣x)\hat y=P(y=1|x) 를 구하고 싶은 것이다.

y^\hat y는 xx가 주어졌을 때 y=1y=1일 확률로 Probability를 나타내며, 식은
y^=σ(w⊤x+b)\hat y = \sigma(w^\top x + b) , where σ(z)=11+e−z\sigma(z)=\frac{1} {1+e^{-z}} 가 된다.

따라서 m개의 training examples

(x(1),y(1)),(x(2),y(2))...(x(m),y(m)){(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}) ... (x^{(m)},y^{(m)})}

이 있을 때, y^(i)≈y(i)\hat y^{(i)} \thickapprox y^{(i)} 인 y^\hat y값을 구하는 것이 목표이다. 맞나?

loss function

손실함수(loss function) 는 모델이 얼마나 잘 작동하는지 확인하기 위한 함수로, single training sample에 적용된다.
y^\hat y와 yy가 비슷하면 loss function의 값이 작아진다.

loss function은 값이 작을수록 좋다.

L(y^,y)=−ylogy^−(1−y)log(1−y^)L(\hat y,y) = -ylog\hat y - (1-y)log(1-\hat y)

y=1y=1이면, L(y^,y)=−logy^L(\hat y,y) = -log \hat y
y=0y=0이면, L(y^,y)=−log(1−y^)L(\hat y,y) = -log(1-\hat y)

따라서 y=1y = 1일 때, y^=1\hat y = 1 에 가까워야 loss가 줄어들고
y=0y = 0일 때 y^=0\hat y = 0 에 가까워야 loss가 낮아진다.

cost function

비용함수(cost function) 는 전체적으로 training 하는데 적용되며
모든 training example에 대한 loss function의 평균이다.

J(w,b)=1m∑i=1mL(y^(i),y(i))J(w,b) = \frac 1 m \sum^m_{i=1} L(\hat y^{(i)},y^{(i)})

Optimization

cost function J(w,b)J(w,b) 을 최소화하기 위한 parameters(w,b)를 찾는 과정이다.

이 과정에서 Gradient Desent 알고리즘을 사용한다

Gradient Descent: Scalar

cost function J(w)J(w)를 minimize 하기 위한 알고리즘.
η\eta : Learning Rate

w=w−η⋅dJ(w)dww = w - \eta · \frac {dJ(w)} {dw}

를 반복적으로 업데이트 하며 dJ(w)dw=0\frac {dJ(w)} {dw} = 0 이 되면 종료한다.

Gradient Descent: Logistic Regression

ddxσ(x)=σ(x)(1−σ(x))\frac d {dx} \sigma(x) = \sigma(x)(1 - \sigma(x))

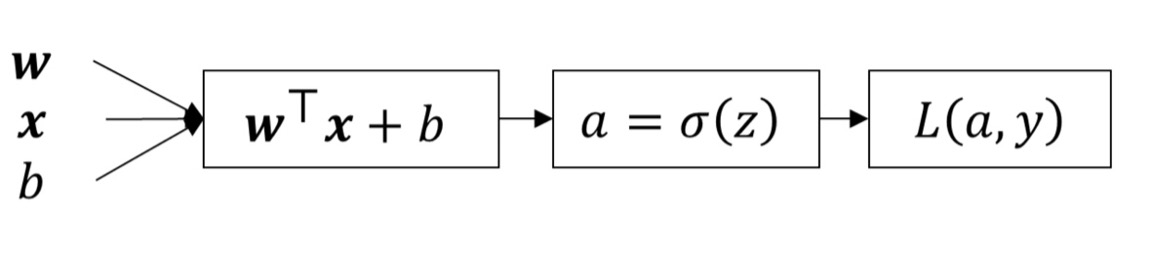
x=[x1x2],w=[w1w2]x = \begin{bmatrix} x_1 \\ x_2\end{bmatrix}, w = \begin{bmatrix}w_1 \\ w_2\end{bmatrix} 일 때

z=w1x1+w2x2+bz = w_1x_1 + w_2x_2 + b
⇓\qquad\qquad \Downarrow
y^=a=σ(z)\qquad \hat y = a = \sigma(z)
⇓\qquad \qquad \Downarrow
L(a,y)\qquad \quad L(a,y)

Derivative

모듈화 후 Chain Rule을 이용해 쪼갠 다음, 전체 network의 미분값을 구할 수 있다.

dLdwi=dLdadadzdzdwi=(−ya+1−y1−a)σ(z)(1−σ(z))xi=(a−y)xi\frac {dL} {dw_i} = \frac{dL}{da} \frac{da}{dz} \frac{dz}{dw_i} = \left(-\frac ya + \frac {1-y}{1-a} \right)\sigma(z)(1- \sigma(z))x_i = (a - y)x_i

따라서 w1, w2, b는 각각

w1:=w1−η⋅dLdw1w_1 := w_1 - \eta · \frac{dL} {dw_1}

w2:=w2−η⋅dLdw2w_2 := w_2 - \eta · \frac{dL} {dw_2}

b:=b−η⋅dLdbb := b - \eta · \frac{dL} {db}

라는 update rule이 적용된다.

이 과정이 한 번의 loss function이 되고, 이것을 m번 반복하여 평균을 낸 것이 J(w)J(w), 즉 cost function 이 된다

참고 :
https://ratsgo.github.io/machine%20learning/2017/04/02/logistic/

https://ko.wikipedia.org/wiki/%EC%9C%84%ED%82%A4%EB%B0%B1%EA%B3%BC:TeX_%EB%AC%B8%EB%B2%95

profile
sue991
AI Researcher

0개의 댓글