WIL_220529_힙, 이진탐색

[힙(heap)]

힙이란

• 우선 순위 큐를 위하여 만들어진 자료구조
• 완전 이진트리 형태의 자료구조
• 파이썬은 최소 힙을 사용

최소힙(Min Heap)은 값이 작은 요소부터 큰 요소 순으로 나열 됨

• 부모 노드 < 자식 노드

힙은 최댓값(최대 힙) 또는 최소값(최소 힙)을 빠르게 찾아 내는데 유리함

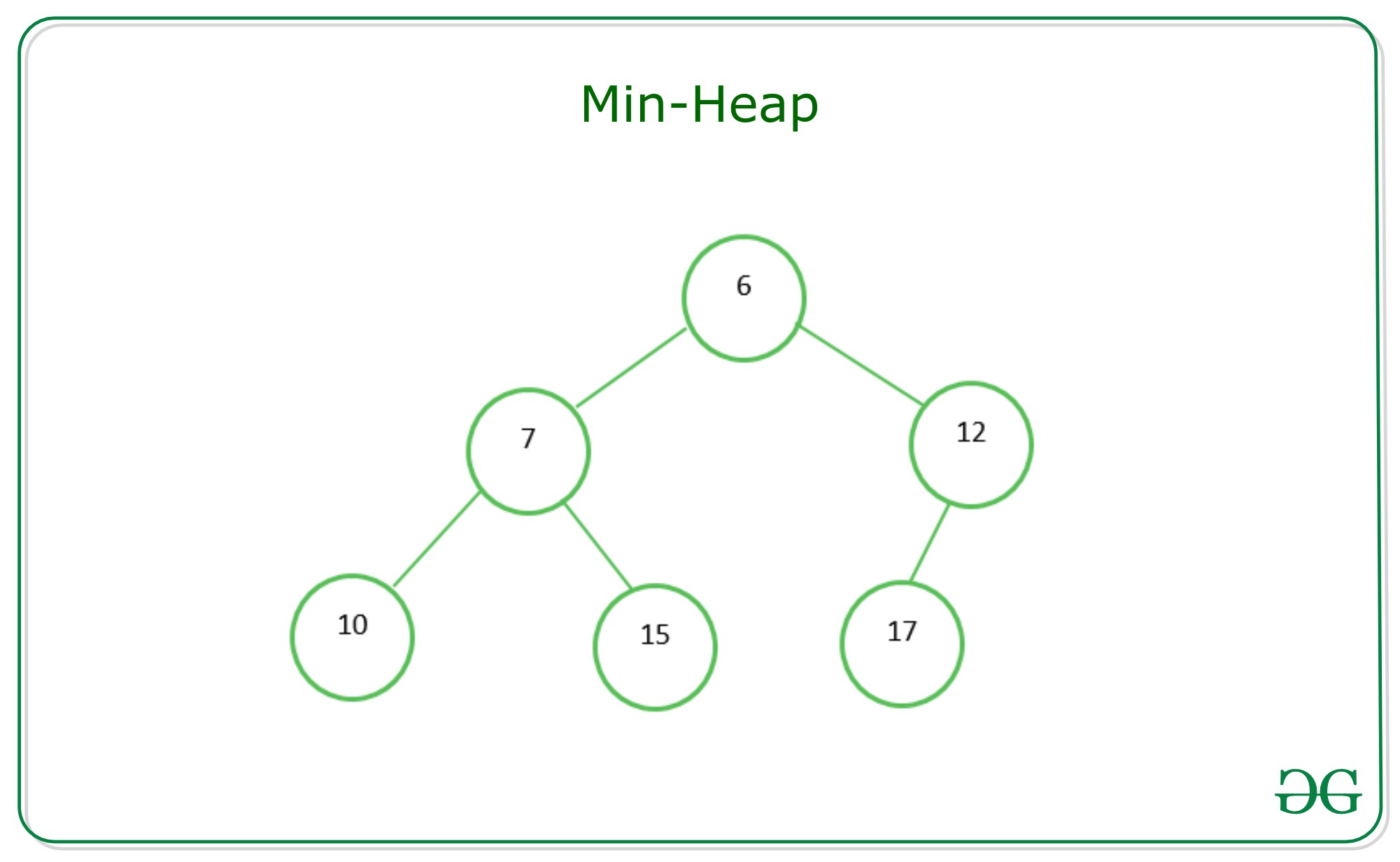
(Min Heap의 구조)

[이진 탐색]

데이터가 정렬 되어 있는 배열에서 특정한 값을 찾아내는 알고리즘

• 배열에 중간에 있는 임의의 값을 선택해 비교를 반복함
• 중간->중간->중간 형식으로 계속해서 중간 범위의 비교를 진행하기에 많은 양에 데이터에서 효율적으로 탐색이 가능
  

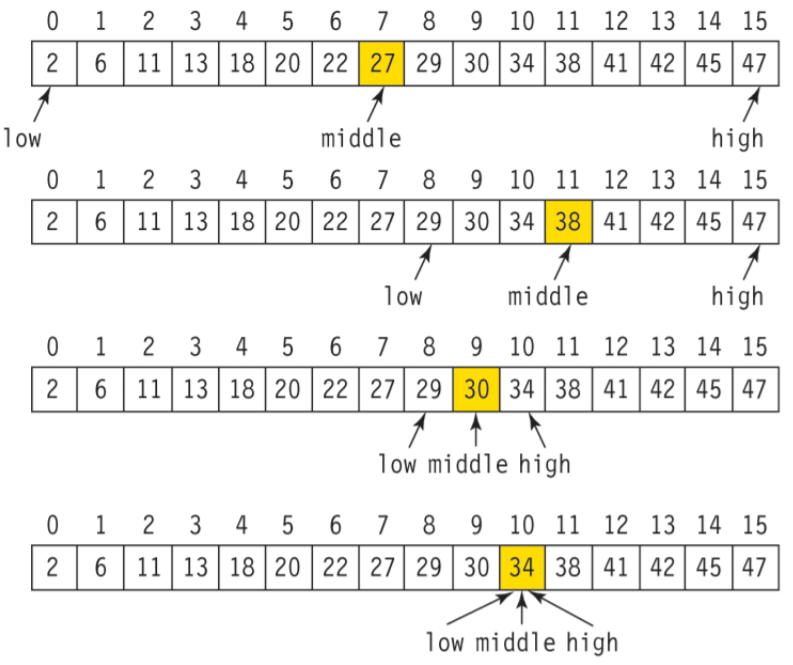
(이진 탐색 동작 방식)

[힙 vs 이진트리]

힙은 최대 값 또는 최소 값을 빠르게 검색하기 위한 구조
이진 탐색 트리는 특정 트리를 빠르게 탐색하기 위한 구조
서로의 지양점과 결이 조금 다름

최소 힙에서 최대 값을 찾으려 하면 성능은 O(n)
최소 힙에서 최소 값을 찾으려 하면 성능은 O(1)
이진 탐색 트리는 O(log n)의 구조를 가짐

import copy
import heapq
import random
import bisect

# sample1 = random.sample(range(1,1000001),1000000)
import time

#sample1 = random.sample(range(1,10000001),10000000)
sample1 = [i for i in range(1,10000001)]
sample2 = copy.deepcopy(sample1)


def test_heap(lst):

    print(heapq.nlargest(1,lst))

def test_bs(lst):
    idx = bisect.bisect_left(lst,10000000)

    if lst[idx] == 10000000:
        print(lst[idx])
    else:
        print(-1)


start_time1 = time.process_time()
test_heap(sample1)
end_time1 = time.process_time()
print(f"작동시간1 : {end_time1 - start_time1}")

start_time2 = time.process_time()
test_bs(sample2)
end_time2 = time.process_time()
print(f"작동시간2 : {end_time2 - start_time2}")

최대 값을 찾기 위한 연습용 코드로 큰 의미는 없음
결과는 다음과 같음

[10000000]
작동시간1 : 0.109375
10000000
작동시간2 : 0.0

탐색이 중점이며, 최소 힙에서 최대 값을 찾으려 했기에 성능 지표에 의미는 없음
다만 힙을 사용해서 수많은 요소 들 중에서 빠르게 찾고자 하는 요소를 찾을 수 있다는 것을 보여줌