이진 탐색/ 이분 탐색(Binary Search)
- 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법
- 시간 복잡도 O(logN)
- 배열 내부 데이터가 정렬되어 있어야만 사용 가능
- 빠르게 데이터 탐색 가능
이진 탐색 원리
- 위치를 나타내는 3개의 변수 "시작점, 끝점, 중간점"을 사용
- 찾으려는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교
예시 - 이진 탐색으로 정렬된 10개의 데이터 중 원하는 데이터 찾기
- 시작점과 끝점 사이에 중간점을 정한다. 중간점이 실수면 소수점 이하는 버린다.
- 중간점 데이터 8 (idx[4])은 찾으려는 데이터 4보다 더 크다.
- 중간점 데이터 이후의 값은 확인할 필요가 없으므로 끝점을 idx[3]으로 옮긴다.

- 시작점은 idx[0], 끝점은 idx[3], 중간점은 idx[1]
- 중간점 데이터 2는 찾으려는 데이터 4보다 작다.
- 중간점 데이터 2이하인 데이터는 확인할 필요가 없으므로 시작점을 idx[2]로 옮긴다.
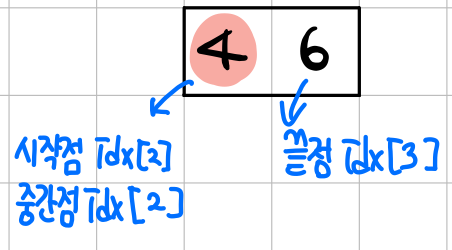
- 시작점은 idx[2], 끝점은 idx[3], 중간점은 idx[2]
- 중간점 데이터와 찾으려는 데이터가 같으므로 탐색 종료
코드 구현 시 기억할 것
- 위치를 나타내는 3개의 변수
- 시작점: 탐색할 가치가 있는 범위의 왼쪽 끝 인덱스
- 끝점: 탐색할 가치가 있는 범위의 오른쪽 끝 인덱스
- 중간점:
(시작점 + 끝점) // 2
- Result: 찾으려는 데이터의 위치
- 이분 탐색에서 자주 하는 실수
- 입력된 배열을 정렬하지 않고 이분 탐색한 경우
- 시작점, 끝점, 중간점, Result 변수의 정의를 헷갈려서 부등호 등을 잘못 쓰는 경우
- 시작점, 끝점 범위를 잘못 설정하거나 Result의 초기값을 잘못 설정하는 경우
기본 구현
def binarySearch(start,end,target,array):
while start <= end:
mid = (start + end) // 2
if array[mid] == target:
return mid
if array[mid] < target:
start = mid + 1
else:
end = mid - 1
return -1




