[section 2] 알고리즘(5) - 순열, 조합, 멱집합

순열 permutation

n개의 요소 중 r개를 중복없이 순서에 상관있게 뽑는 경우의 수 = nPr

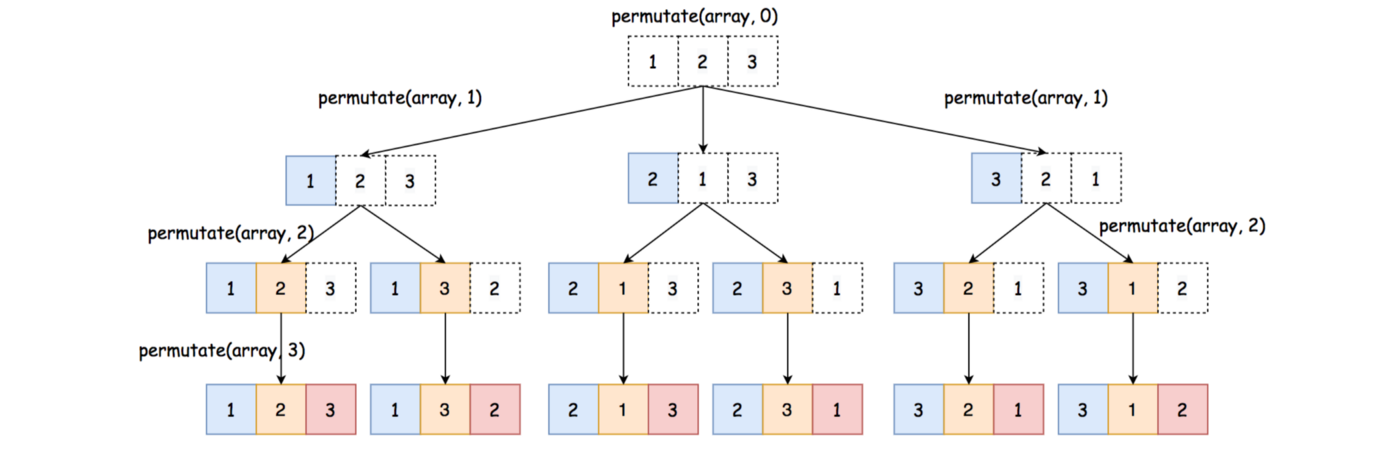
일반식

nPr = n! / (n-r)!

코드

// arr : 요소
// output : 경우의 수
// visited : 중복 방지
private void permutation(int[] arr, int[] output, boolean[] visited, int n, int r) {
	if (r== 0) {
		System.out.println(Arrays.toString(output));
		return;
	}
    for (int i = 0; i < n; i++) {
    	if (!visited[i]) {
        	visited[i] = true;
            int[] newOutput = Arrays.copyOf(output, output.length + 1);
            newOutput[newOutput.length - 1] = arr[i];
            permutation(arr, newOutput, visited, n, r - 1);
            visited[i] = false;
		}
	}
}

---

조합 combination

n개의 요소 중 r개를 중복없이 순서에 상관없이 뽑는 경우의 수 = nCr

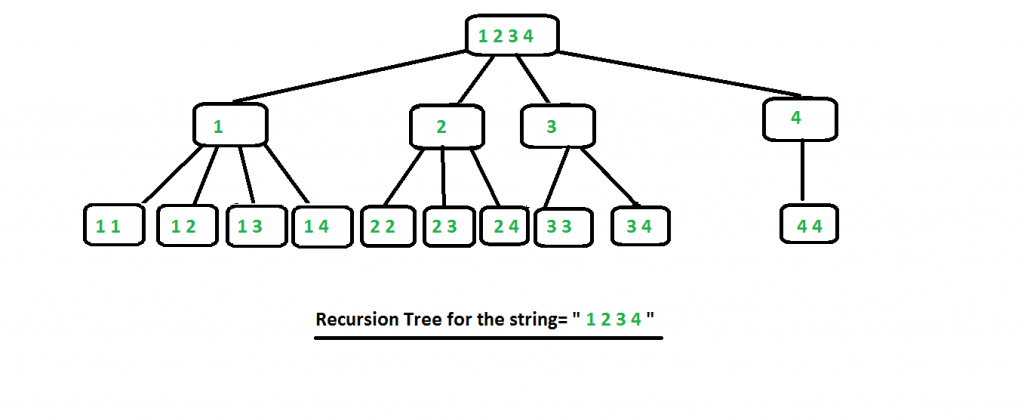
일반식

nCr = n! / (r! x (n-r)!)

코드

// arr : 요소
// output : 경우의 수
// visited : 중복 방지
// start : 이미 뽑힌 요소를 다시 뽑지 않기 위해
private void combination(int[] arr, int[] output, boolean[] visited, int n, int r, int start) {
	if (r== 0) {
		System.out.println(Arrays.toString(output));
        return;
	}
    for (int i = start; i < n; i++) {
    	if (!visited[i]) {
        	visited[i] = true;
            int[] newOutput = Arrays.copyOf(output, output.length + 1);
            newOutput[newOutput.length - 1] = arr[i];
            combination(arr, newOutput, visited, n, r - 1, i + 1);
            visited[i] = false;
		}
	}
}

---

멱집합 power set

주어진 집합의 모든 부분 집합으로 구성

코드

// stack : 선택된 부분집합
private static void powerSet(int[] arr, Stack<Integer> stack, int idx) {
	// 마지막 요소까지 순회한 경우
	if (idx >= arr.length)  {
    	System.out.println(stack.toString());
        return;
    }
    // 부분집합에 포함되지 않은 경우
    // 부분집합에 넣고 재귀호출
    stack.push(arr[idx]);
    powerSet(arr, stack, idx + 1);
    // 부분집합에 포함된 요소를 하나씩 제거 후 재귀호출
    stack.pop();
    powerSet(arr, stack, idx + 1);
}

참고