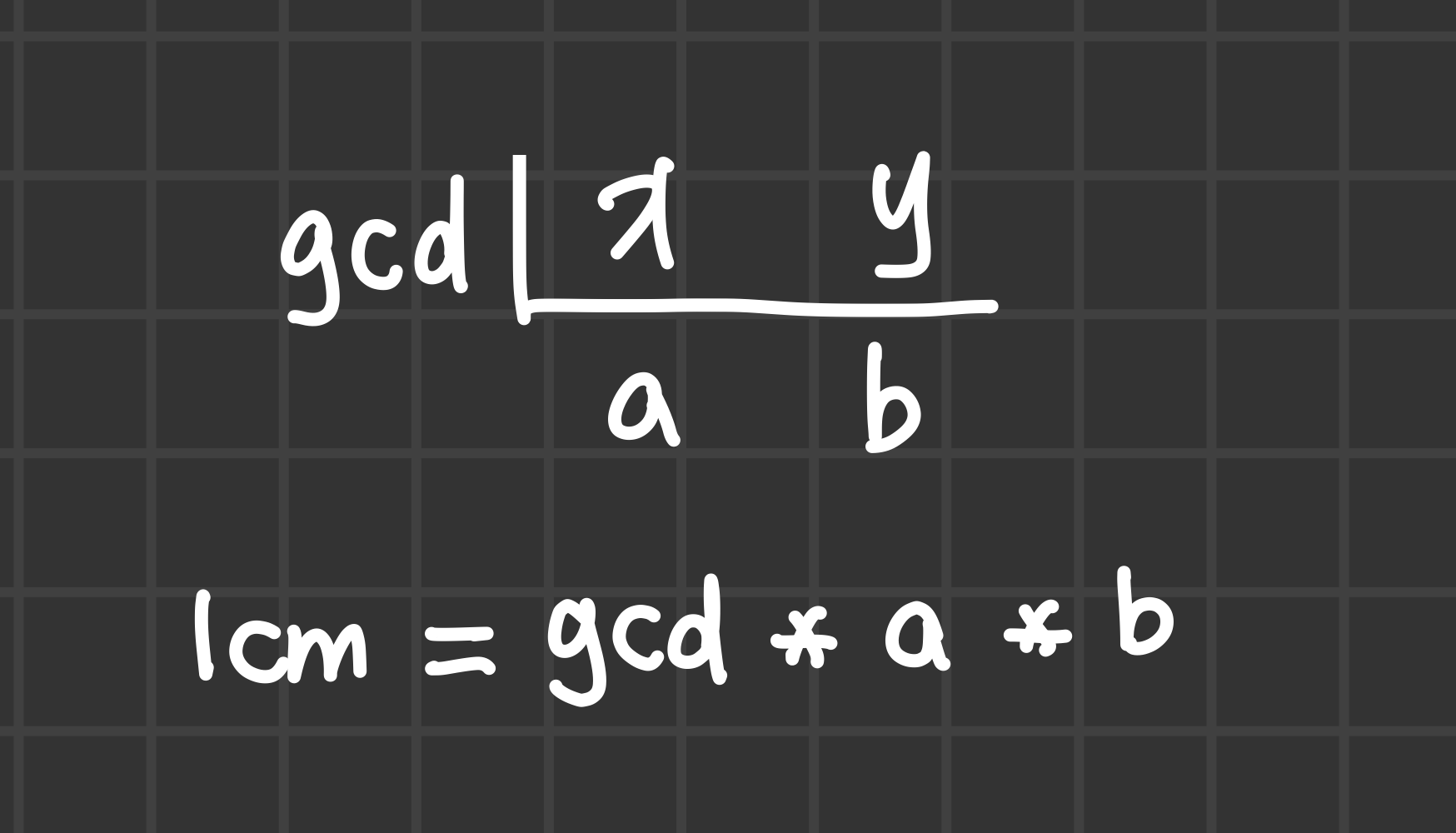풀이
최대공약수 gcd
최소공배수 lcm
x와 y의 최대공약수가 gcd이고 최소공배수가 lcm
gcd * a = x, gcd * b = y 라고 하면
a * b = lcm / gcd
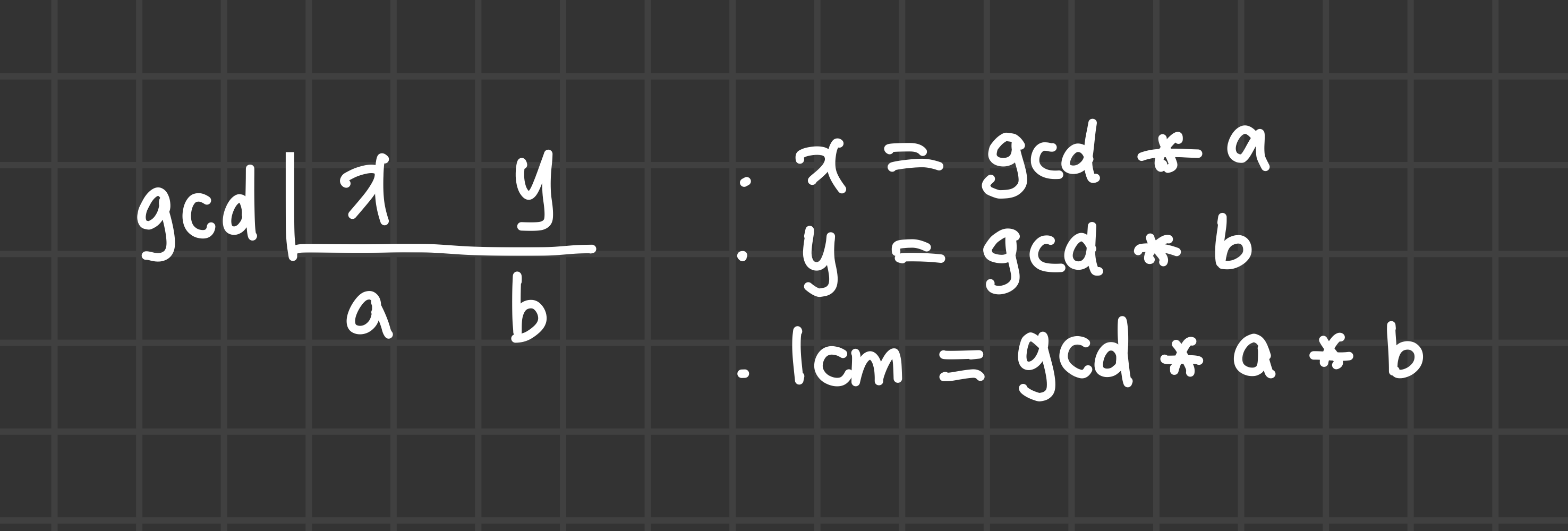
따라서 (a * b = lcm / gcd) 를 만족하는 (a, b) 쌍을 찾아서 x, y를 구해주면 된다.
ex) gcd = 6, lcm = 180 인 경우, a * b = 30이므로
(a, b) 쌍은 (1, 30), (2, 15), (3, 10), (5, 6) 이 있다.
이에 만족하는 (x, y)쌍은 (6, 180), (12, 90), (18, 60), (30, 36)이다.
이 중 x + y가 가장 작은 값은 30, 36이다!
.
.
.
로 끝나는 줄 알았는데 계속해서 답이 틀렸고,
틀린 x, y의 gcd를 구해보니 원래의 gcd가 나오질 않았다
대체 왜냐..................... 아무리 생각해도 모르겠음..........
그래서 일단 if gcd(x, y) == g 조건을 넣어서 해결함.......
근데 찝찝하다.......................
코드
from math import sqrt, gcd
g, l = map(int, input().split())
n = l // g
for a in reversed(range(1, int(sqrt(n)) + 1)):
if n % a == 0:
x = g * a
y = g * (n // a)
if gcd(x, y) == g:
print(x, y)
break