[백준][1260] DFS와 BFS

suhan0304·2023년 10월 31일

BFS DFS 백준

백준

목록 보기

4/53

Problem Link : https://www.acmicpc.net/problem/1260

문제

그래프가 있다고 할 때 DFS 방식과 BFS 방식으로 탐색한 결과를 출력한다.

DFS는 Depth-First Search로 깊이 우선 탐색이라 한다.
BFS는 Breadth-First Search로 너비 우선 탐색이라 한다.
```
용어의 정의를 알면 어느 정도 감이 잡히므로 영어로 된 용어도 외울 수 있으면 외우도록 하자.
```

입력

정점의 개수 N, 간선의 개수 M, 탐색 시작 정점 V
다음 M 개의 줄, 간선이 연결하는 두 정점의 번호

출력

첫째 줄, DFS 수행한 결과
둘째 줄, BFS 수행한 결과

풀이에 앞서

DFS와 BFS의 개념은 굉장히 중요하고 자주 사용하는 개념이기 때문에 자세하게 알면 알수록 좋다. DFS, BFS 개념이 헷갈리고 정립이 안 됐다면 이 문서를 다시 한 번 정독 하자.

DFS(Depth-First Search) 깊이 우선 탐색

깊이 우선 탐색이란?

깊이 우선 탐색이란 루트 노드(정점)에 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법
- 미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 가다가 더 이상 갈 수 없 게 되면 다시 가장 가까운 갈림길로 돌아와서 다른 방향으로 다시 탐색을 진행하는 방법과 유사하다.
- 즉, 넓게(wide) 탐색하기 전에 깊게(deep) 탐색하는 것이다.
- 사용하는 경우 : 모든 노드를 방문하고자 하는 경우에 이 방법을 선택한다.

깊이 우선 탐색의 특징

깊이 우선 탐색은 아래와 같은 특징을 가지고 있다.
- 자기 자신을 호출하는 순환 알고리즘 형태를 가지고 있다.
- 전위 순회(Pre-Order Traversals)를 포함한 다른 형태의 트리 순회는 모두 DFS의 한 종류이다.
- 깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단하다.
- 단순 검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느리다.

깊이 우선 탐색의 과정

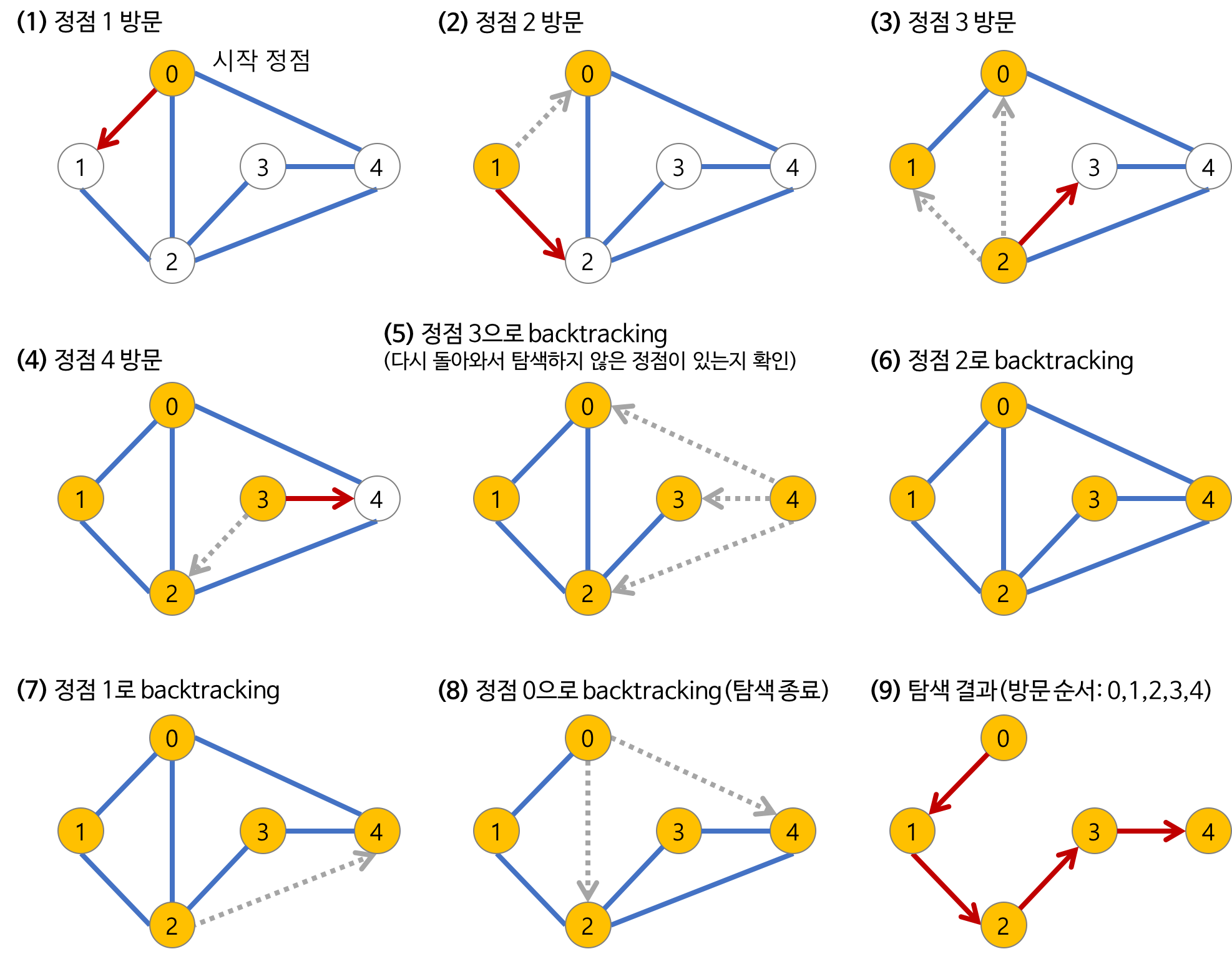
시작 노드를 방문한다.
- 방문한 노드를 방문했다고 표시한다.
시작 노드와 인접한 노드들을 차례로 순회한다.
이 때 인접한 노드를 방문했다면, 방문한 노드와 인접한 노드들 또한 전부 방문해야 한다.
- 두 번째 방문한 노드를 정점으로 다시 DFS를 시작하여 이웃 노들들을 방문한다.
추가로 방문한 노드의 분기를 전부 완벽하게 탐사했다면 다시 기존 노드들로 돌아가 방문이 안된 정점을 찾는다.
- 한 분기를 완벽하게 탐색한 뒤에야 다시 인접한 다른 분기를 방문할 수 있다는 뜻이다.
- 방문이 안 된 정점이 없으면 종료한다.
- 방문이 안 된 정점이 있다면 해당 정점을 시작 정점으로 DFS를 시작한다.

BFS(Breadth-First Search) 너비 우선 탐색

너비 우선 탐색이란?

너비 우선 탐색이란 루트 노드(정점)에서 시작해서 인접한 노드를 먼저 탐색하는 방법이다.
- 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법이다.
- 즉, 깊게(deep) 탐색하기 전에 넓게(wide) 탐색하는 것이다.
- 사용하는 경우 : 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 이 방법을 선택

너비 우선 탐색의 특징

너비 우선 탐색은 아래와 같은 특징을 가지고 있다.
- 직관적이지 않다. (시작 노드에서 시작해서 거리에 따라 단계별로 탐색한다.)
- 어떤 노드를 방문했었는지 여부를 반드시 검사 해야한다.
  - 이를 검사하지 않을 시 무한 루프에 빠질 위험이 있다.

너비 우선 탐색의 과정

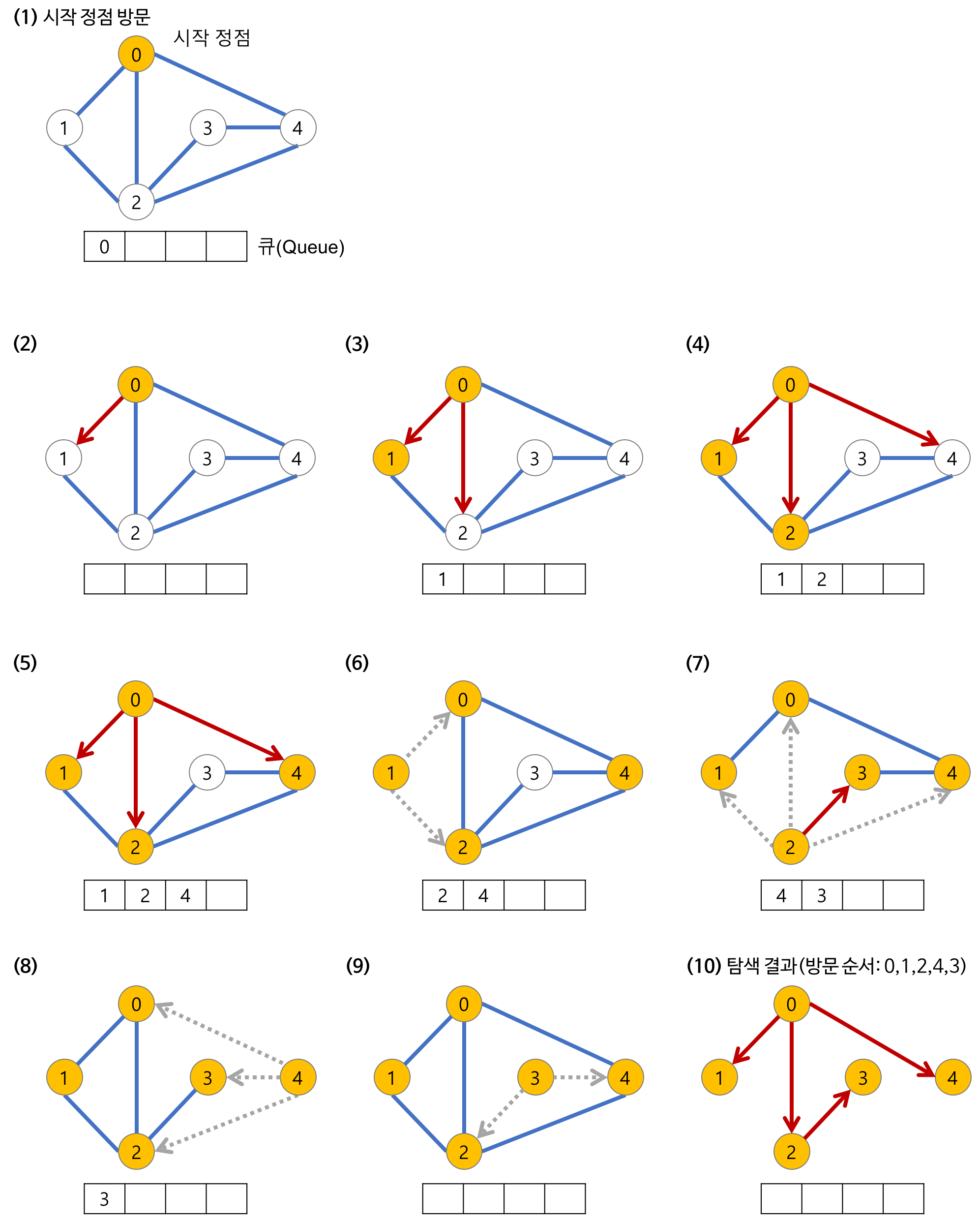
시작 노드를 방문한다. (방문한 노드 체크)
- 큐에 방문된 노드를 삽입(enqueue)한다.
- 초기 상태의 큐에는 시작 노드만이 저장
큐에서 꺼낸 노드와 인접한 노드들을 모두 차례로 방문
- 큐에서 꺼낸 노드를 방문한다.
- 큐에서 꺼낸 노드와 인접한 노드들을 모두 방문한다.
  - 인접한 노드가 없다면 큐의 앞에서 노드를 꺼낸다(dequeue).
- 큐에 방문된 노드를 삽입(enqueue)한다.
큐가 소진될 때까지 계속한다.

DFS, BFS 구현 방법

DFS	BFS
1. 순환 호출 이용	큐를 이용
2. 명시적인 스택이용

파이썬의 경우 큐, 스택을 활용하기 위해서 List와 deque(popleft를 활용해 스택처럼 사용) 자료형을 이용할 수 있는데 이때 deque를 사용하는 것이 List를 사용하는 것보다 성능적인 측면에서 유리하다. 또한 List에서는 없는 popleft, appendleft 메서드를 사용할 수 있다는 장점이 있다.

풀이

위의 구현 방법을 토대로 DFS는 순환 호출(재귀 함수)를 이용하여 코딩, BFS는 파이썬의 List 자료형을 이용해 구현하였다.

DFS는 다음과 같이 구현

def dfs(graph, v, visited):
   visited[v] = True
   for i in graph[v]:
       if not visited[i]:
           dfs(graph, i, visited)
   return

def dfs(graph, v):
   graph[v][v] = -1  # 방문한 노드는 방문했다고 표시
   print(v, end=" ")
   for i in range(1, n + 1):
       # 간선이 있고, 해당 노드에 방문학 적이 없다면
       if graph[v][i] == 1 and graph[i][i] != -1:
           dfs(graph, i)  # 재귀를 사용해 dfs 구현
   return

BFS는 다음과 같이 구현

def bfs(graph, v):
    queue = []  # bfs는 큐를 이용해서 쉽게 구현
    queue.append(v)
    graph[v][v] = -1  # 방문한 노드는 방문했다고 표시
    while queue:  # 원소가 하나라도 있을시 True, 원소가 하나도 없으면 False
        v = queue.pop(0)
        print(v, end=" ")
        for i in range(1, n + 1):
            # 간선이 있고, 해당 노드에 방문학 적이 없다면
            if graph[v][i] == 1 and graph[i][i] != -1:
                queue.append(i)
                graph[i][i] = -1  # 방문한 노드는 방문했다고 표시
    return

이 때 방문했다는 사실을 따로 변수를 만들지는 않고 graph의 대각 원소를 방문했다는 사실을 파악하기 위해 사용한다.

다른 변수를 사용해서 방문 여부를 파악해도 전혀 지장이 없다.
만약, 방문한 노드를 또 여러 번 방문 할 수 있는 문제가 나오면 방문 여부를 파악하는 변수를 추가적으로 작성해줘야한다.

코드

def dfs(graph, v):  # 순환 함수 말고도 stack 형식을 이용해서 구현해낼 수 있다.
    graph[v][v] = -1  # 방문한 노드는 방문했다고 표시
    print(v, end=" ")
    for i in range(1, n + 1):
        # 간선이 있고, 해당 노드에 방문학 적이 없다면
        if graph[v][i] == 1 and graph[i][i] != -1:
            dfs(graph, i)  # 재귀를 사용해 dfs 구현
    return


def bfs(graph, v):
    queue = []  # bfs는 큐를 이용해서 쉽게 구현
    queue.append(v)
    graph[v][v] = -1  # 방문한 노드는 방문했다고 표시
    while queue:  # 원소가 하나라도 있을시 True, 원소가 하나도 없으면 False
        v = queue.pop(0)
        print(v, end=" ")
        for i in range(1, n + 1):
            # 간선이 있고, 해당 노드에 방문학 적이 없다면
            if graph[v][i] == 1 and graph[i][i] != -1:
                queue.append(i)
                graph[i][i] = -1  # 방문한 노드는 방문했다고 표시
    return


n, m, v = map(int, input().split())

graph = [[0 for _ in range(n + 1)] for _ in range(n + 1)]
for _ in range(m):
    v1, v2 = map(int, input().split())
    graph[v1][v2] = graph[v2][v1] = 1

dfs(graph, v)

for i in range(1, n + 1):
    graph[i][i] = 0

print()
bfs(graph, v)

참고 자료

수정

23.11.01 / 구현 방법 추가 설명 작성

suhan0304

Be Honest, Be Harder, Be Stronger

이전 포스트

[백준][1707] 이분 그래프

다음 포스트