<Reference>
오토인코더의 모든 것 - 1/3

GAN리뷰를 마치고 같은 플레이 리스트의 오토인코더의 모든 것 강의를 듣기 시작했다! 여행 가기전에 다 듣고 가고싶었지만 맘이 붕뜨는 바람에 다 못들었었는데, 일단 Autoencoder의 introduction을 위한 Deep learning basic revisit과 Manifold learning 파트까지는 들었기 때문에 유럽행 경유지인 홍콩 공항에서 지금까지 들은 부분 먼저 올려보자,, 해서 올리는 글! 다음 비행기까지 2시간이나 남았는데 유튜브나 넷플릭스는 더이상 보기 싫어서 뒷부분 강의도 들어보려구 한다,,, 팟팅,,,

Autoencoder → purpose of nonlinear dimensionality reduction

🤷‍♂️ nonlinear dimensionality reduction?

• Representation learning
• Feature extraction
• Manifold learning

Autoencoder’s 4 Main keywords

1. Unsupervised Learning → 학습 방법
2. Manifold Learning → encoder : 차원 축소의 역할
3. Generative Model Learning → decoder : 생성 모델의 역할
4. ML(Maximum Likelihood) Density Estimation → Loss function : negative ML

• 입력과 출력이 같은 결과를 내도록 하는 구조

1. Revisit Deep Neural Networks

Machine learning problem

Classical Machine Learning

1. collecting training data

2. define functions

   1. output
   2. Loss function

3. learning/training

   1. loss가 최소화되는 optimal parameter 찾기

4. predicting/testing

   1. optimal function output계산

   *Note. 고정된 입력값에 대한 고정된 출력값 생성

⇒ Deep Neural Networks

1. collecting training data
2. define function
   1. Deep Neural Net
      1. 네트워크 구조
      2. 레이어 수
   2. Loss function
      1. MSE, CrossEntropy
   • Backpropagation을 통해 DNN을 학습시키기 위한 조건들 Assumption1. Total loss of DNN over training samples is the sum of loss for each training sample : training DB의 전체 샘플들의 각 loss의 합을 DNN의 total loss로 본다. Assumption2. Loss for each training example is a function of final output of DNN : loss function의 입력은 정답과 네트워크의 출력값 두가지로만 이루어져있다.
     
3. learning/training

   1. Gradient descent

      $\theta^* = \text{argmin }_{\theta \in \Theta} L(f_{\theta}(x),y)$

   2. Iterative Method : step by step

      1. How to update $\theta → \theta+\Delta \theta$ ⇒ Only if $L(\theta+\Delta \theta) < L( \theta)$ : Loss가 줄어들 때
      2. when to stop search ⇒ If $L(\theta+\Delta \theta) == L( \theta)$ : Loss의 변동이 없을 때
      3. How to find $\Delta \theta$ so that $L(\theta+\Delta \theta) < L( \theta)$ ⇒ $\Delta \theta = -\eta \nabla L$ where $\eta > 0$ : learning rate
      • 어떻게 $\theta$를 업데이트 해야 Loss 값이 줄어드는지? $\small L(\theta+\Delta\theta) = L(\theta)+\nabla L \cdot\Delta\theta + \text{second derivative} + \text{third derivative} + \dots$ → Taylor Expansion $\small L(\theta+\Delta\theta) \approx L(\theta)+\nabla L \cdot\Delta\theta$ → Approximation : 더 많은 미분 차수를 사용할 수록 더 넓은 지역을 작은 오차로 표현 가능 $\small L(\theta+\Delta\theta)-L(\theta) = \Delta L = \nabla L \cdot\Delta\theta$ → $\Delta L <0$ 이어야함 If $\Delta \theta = -\eta \nabla L$, then $\Delta L = -\eta ||\nabla L||^2 < 0$, where $\eta > 0$ and called learning rate *$\nabla L$ = gradient of L, steepest increasing direction of $L$
        

   3. parameter들에 대해 Loss function의 미분이 필요 → Backropagation

      1. Error at output layer

         $\delta^L = \nabla_aC\odot\sigma'(z^L)$
         • $C$ : Cost(Loss)
         • $a$ : final output of DNN
         • $\sigma(\cdot)$ : activation function
         • 가장 마지막 출력단의 error signal을 구하는 과정 → loss를 network 출력값에 대해 미분 : $\nabla_aC$ & activation function의 미분에 feedfoward 값을 넣은 값 element-wise product

      2. Error relationship between two adjacent layers → 바로 앞레이어와의 error relationship을 통해 가장 앞 레이어의 loss까지 구함

         $\delta^l = \sigma'(z^l)\odot\left( \left(w^{l+1} \right)^T\delta^{l+1}\right)$

      3. Gradient of C in terms of bias

         $\nabla_{b^l}C = \delta^l$

      4. Gradient of C in terms of weight

         $\nabla_{W^l}C = \delta^l(a^{l-1})^T$

      Neural networks and deep learning

4. predicting/testing

Loss function viewpoints I : Backpropagation

• Backpropagation이 얼마나 잘 동작하는가의 관점에서는 MSE < Cross Entropy Loss
• Maximum Likelihood 관점 : output의 형태에 따라
  • continuous value : MSE
  • discrete value : Cross Entropy Loss

Type 1. Mean Square Error / Quadratic loss

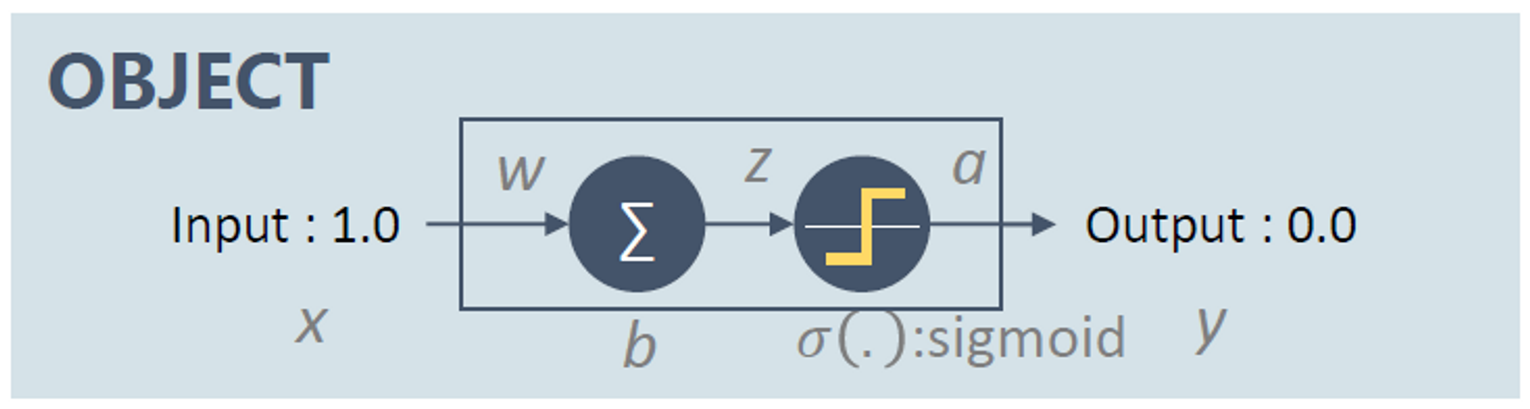
• Loss $C$ = MSE ⇒ (입력-정답)^2/2

• $\nabla_aC$ : C를 a에 대해 미분

• $\delta$ : error signal

• $\frac{\partial C}{\partial w} = x\delta = \delta$ → $w = w-\eta\delta$

• $\frac{\partial C}{\partial b} = \delta$ → $b=b-\eta\delta$

• Gradient Vanshing problem

  • 출력 레이어에서의 에러값에 activation function 의 미분값이 곱해지는데($\sigma'(z^L)$), 이때 그 값이 0에 가까워질 경우, error signal($\delta$)도 0에 가까워져 레이어간 업데이트가 전혀 이루어지지 않게 된다.
  • 초기값의 영향을 크게 받는다!

Type 2. Cross Entropy

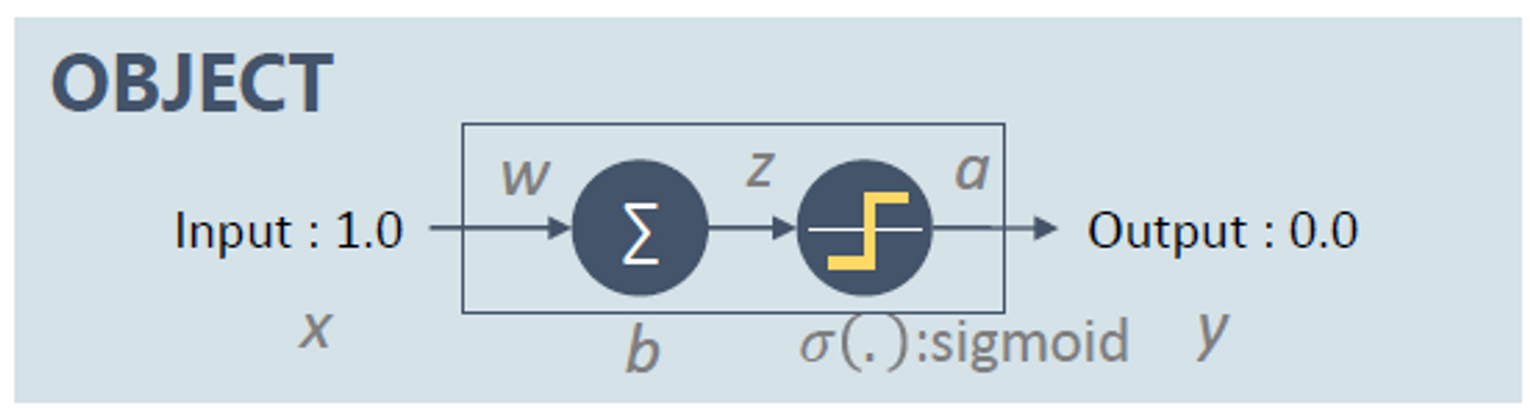
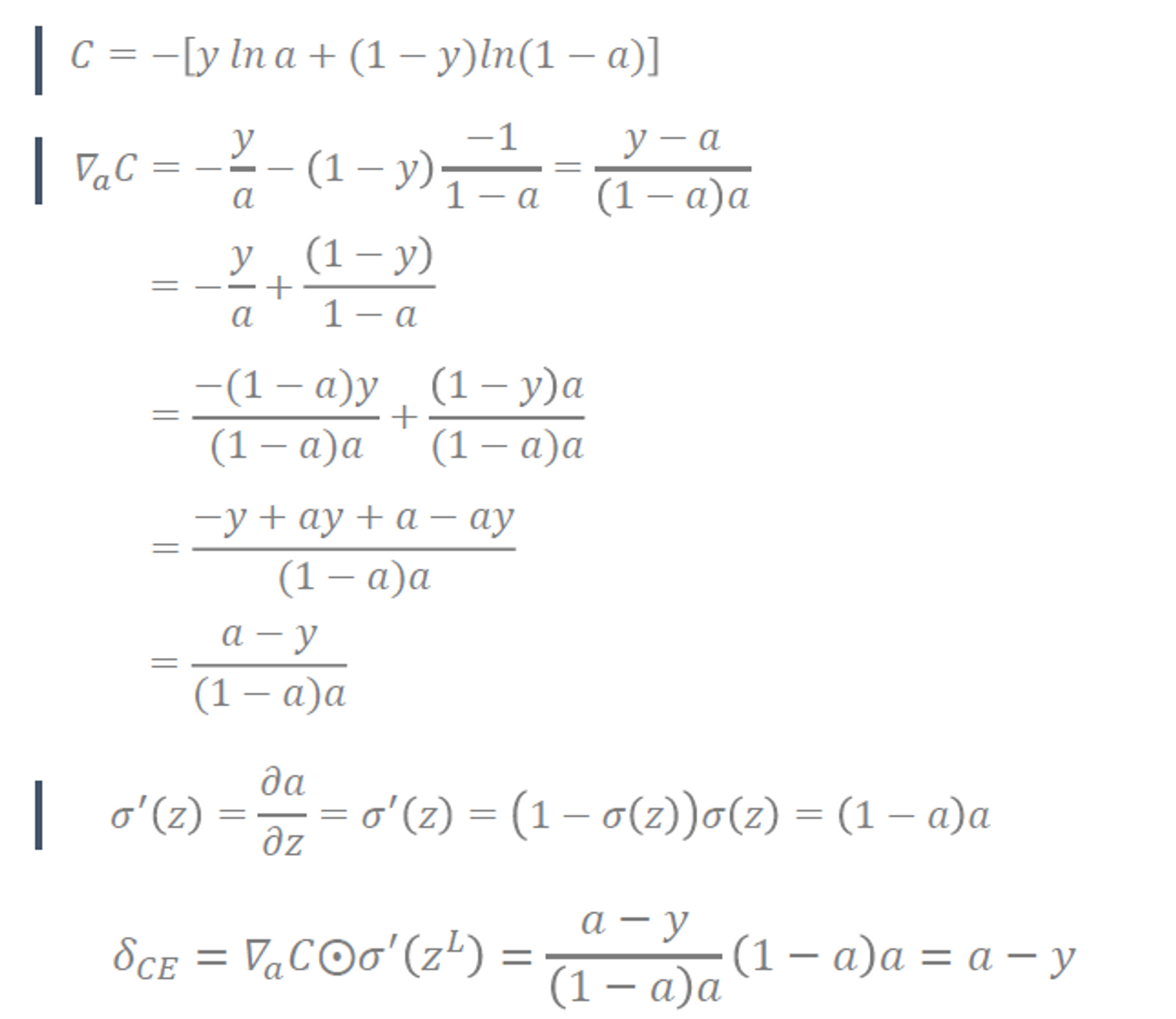
• Cross Entropy의 출력 layer의 error signal($\delta$)는 $\sigma'(z^L)$ term자체가 사라져서 gradient vanishing problem에서 자유로운 편, 초기값의 영향이 적다.
  • btw, 레이어를 여러개 사용하면 결국 activation function 의 미분값이 계속해서
    곱해지므로 gradient vanishing problem에서 완전히 자유로운건 아님.

Loss function viewpoints II : Maximum likelihood

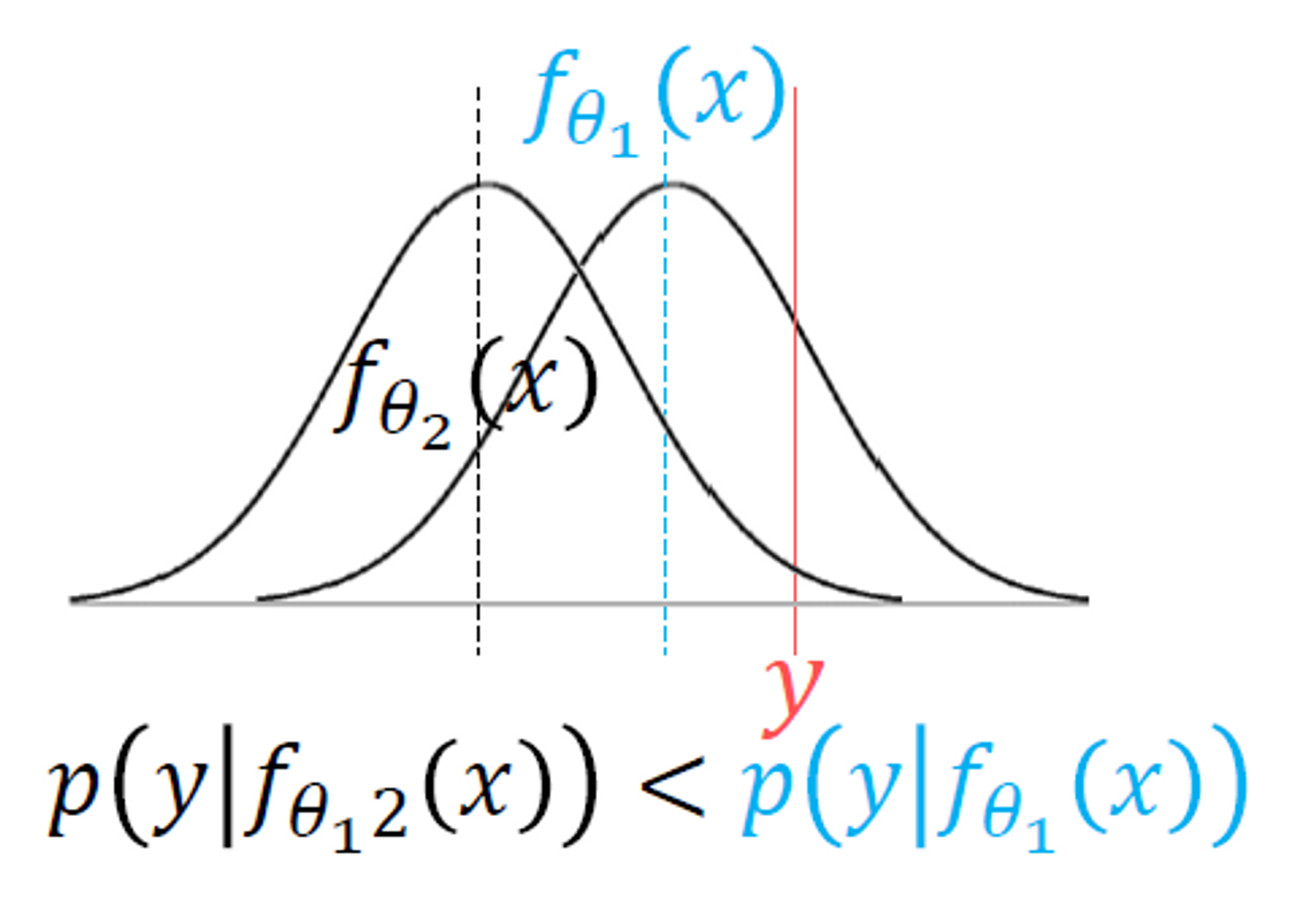
• x축 : 특정 값 → 모델의 출력, 정답 등,,,
• y축 : 해당 값이 분포에서 등장할 확률
• 분포 : 가정한 분포, 특정 값이 해당 모델에서 도출될 확률 분포
• 어떤 파라미터의 모델이 있을 때, 그때의 출력값으로 정답 y의 확률을 높이는 모델인지 보고, 그 확률을 최대화하는 과정
• 결국에는 가장 높은 확률을 갖는 평균과 정답 y가 일치하게 되는 것이 목표
• 그렇게 모델의 최적 확률 분포를 찾게 되면, 그 분포에서의 sampling을 통해 y와 비슷하지만 다른 어떤 값을 생성하는 과정으로 이어지게 됨

Conditional probability $p$가 어떤 분포를 따르는지 가정하에 다음을 진행 → ex. Gaussian Dist.

$p\left(y|f_{\theta}\left(x\right)\right)$ → Network출력값이 $f_{\theta}\left(x\right)$로 주어졌을 때, 정답 $y$가 나올 확률이 최대화 되어야함

• Network출력값 $f_{\theta}\left(x\right)$ : Conditional probability $p$를 추정하기 위한 parameter 개념(ex. Gaussian의 경우 평균값,,,)

log-likelihood

loss : $-\log \left( p \left(y|f_{\theta}\left (x\right )\right)\right)$

주어진 데이터를 가장 잘 설명하는 모델 찾기 → Maximum log-likelihood되는 파라미터

$\theta^* = \argmin_\theta[-\log \left( p \left(y|f_{\theta}\left (x\right )\right)\right)]$

⇒ Conditional probability $p$의 분포의 parameter를 찾은 것 ⇒ 확률 분포를 찾은 것 → sampling이 가능하다!

*Extension. 생성모델

확률 분포에서 sampling을 통해 새로운 input을 만들어 낼 수 있고, 새로운 출력이 나오게 된다.

$y_{new} \sim p(y|f_{\theta^*}\left(x_{new}\right))$

$\text{i.i.d Condition on }p \left(y|f_{\theta}\left (x\right )\right)$

Assumption1. Independece : train db모두의 conditional prob가 아닌 각 sample($D_i$)의 conditional prob의 곱으로 추정

Assumption2. Identical Distribution : 모든 샘플의 distribution을 같다고 가정

⇒ 결론 : 두개의 가정을 모두 만족

분포를 다음 두가지로 가정해볼 수 있음 (일변수 - Univariate)

• Gaussian Distribution의 경우 MSE
• Bernoulli Distribution의 경우 Cross-Entropy

각각과 같이 loss가 정리된다.

다변수의 경우도 마찬가지.

• Autoencoder
  • $p(x|x)$
  • network 입력 x일때 출력도 입력과 같아지는것이 목표
• Variational Autoencoder
  • $p(x)$
  • training db의 확률분포 그 자체를 추정

2. Manifold Learning

Definition

Visualize의 편의성을 위해 고차원 데이터($R^m$)를 저차원 데이터($R^d$)로 차원 축소할 때,

Manifold : 고차원 데이터 포인트들을 error없이 잘 아우르는 subspace가 있을 것. 그것을 manifold라고 하고, maifold에서 projection하게되면 저차원 데이터로 매핑할 수 있을 것.

Four objectives

1. Data visualization
2. Curse of dimensionality
   • 차원이 증가할수록, 공간내 샘플의 수가 매우 희박해진다
   • Manifold Hypothesis(assumption)
     • 샘플을 아우르는, 잘 밀집된 저차원의 subspace(=Manifold)를 잘 찾으면, 해당 Manifold를 벗어나면 밀도가 매우 희박해진다.
3. Discovering most important features
   • Manifold 좌표들이 조금씩 변화할 때 원래 데이터도 조금씩 변함을 확인
   • New distance metric → Euclidean distance ≠ Manifold의 distance ⇒ dominant한 feature representation상 가까운 sample들을 찾을 수 있음, 의미적인 interpolation이 가능하다
   • Entangled Manifold vs. Disentangled Manifold
     • dominant feature를 잘 capture했을 경우 disentangled manifold의 형태가 됨을 확인할 수 있음

Dimension reduction

Texonomy

1. Linear
   1. PCA
   2. LDA
2. Non-linear
   1. AE
   2. t-SNE

이중에서도 Non-linear dimension reduction method에 해당하는 Autoencoder에 대해 앞으로 더 자세히 알아볼 예정!