"Message-passing GNNs are known to suffer from pathologies, such as oversmoothing, due to their repeated aggregation of local information [19], and over-squashing, due to the exponential blow-up in computation paths as the model depth increases [1]. As a result, there is a growing interest in deep learning techniques that encode graph structure as a soft inductive bias, rather than as a hard-coded aspect of message passing [14, 24]."
- Rethinking Graph Transformers with Spectral Attention. NeurIPS 2021 -*

Abstract

Graph representation learning에서 Transformer가 좋은 성능을 보이는가?

Graphormer

• standard transformer architecture
• 많은 graph representation learning task에서 좋은 성능을 보임
  • especially on the recent OGB Large-Scale Challenge

Key Insight

• graph를 모델링하기위해 structural information을 효율적으로 encoding하는 방법의 필요성
• Graphormer의 표현력을 수학적으로 characterize
  • graph의 structural information을 encoding하는 방법을 다른 GNN variants와 비교해보았을 때, 이들을 모두 Graphormer의 특수케이스로 커버할 수 있었음

💡 Ways to encode structural information of the graph ⇒ Graphormer

1. Introduction

Graph representation에 transformer를 적용하고자 하는 꾸준한 시도

• 하지만 지금까지 가장 효과적인 방법은 feature aggregation과 같은 classic GNN variants의 몇몇 key module에만 softmax attention을 적용하는 방식 (ex. GAT) → graph representation learning에 transformer 를 적용하는것이 적절한가?
  

Graphormer

• directly built upon the standard transformer architecture
• graph-level prediction task에서의 SOTA(OGB-LSC)

node $i$의 self-attention

• 노드쌍 사이의 relation으로 확인할 수 있는 structural information을 고려하지 않음
• node $i$와 다른 노드들 사이의 semantic similarity만 계산

다음 information들을 활용해 structural encoding method 구성

1. Centrality Encoding

• 목적 : 그래프에서의 node importance

☹️ self-attention의 경우 node의 semantic feature의 유사도를 기반으로 계산되기 때문에, 다른 노드들보다 더 중요한 노드의 중요도같은 정보를 파악하기 어려움

💡 degree centrality

• 학습가능한 벡터가 노드의 degree에 따라 각 노드에 할당되고, 이것이 input layer의 node feature들에 더해지는 방식

연결 중심성(Degree Centrality)
: 한 Node에 연결된 모든 Egde의 갯수(Weighted 그래프일 경우에는 모든 Weight의 합)로 중심성을 평가

1. Spatial Encoding

• 목적 : 노드들 사이 structural relation

☹️ graph-structured data는 이미지나 자연어같은 structured data와는 달리 임베딩 하기위한 canonical grid(표준 격자)가 없음

• 노드들은 non-Euclidean space에 엣지로 연결되어 존재함

💡 각 노드쌍에 대해 spatial raltion을 기반으로한 학습가능한 임베딩 주기

• shortest path
  • softmax attention의 bias term으로 encoded
  • additional info : edge feature(ex. 분자구조에서 두개의 원자사이 연결의 종류)를 포함하기도 함

각 노드쌍에 대해 learnable embedding(shortest path)과 edge feature의 dot product 평균을 계산해 attention module에 사용

2. Preliminary

Graph Neural Network (GNN)

• AGGREGATE : 이웃노드의 정보 aggregation
• COMBINE : 노드 representation에 이웃노드로 부터 aggregation한 정보를 융합
• READOUT : 노드 feature를 final representation에 aggregate, by permutation invariant function

Transformer

• Query
• Key
• Value

Self-Attention

3. Graphormer

3.1 Structural Encodings in Graphormer

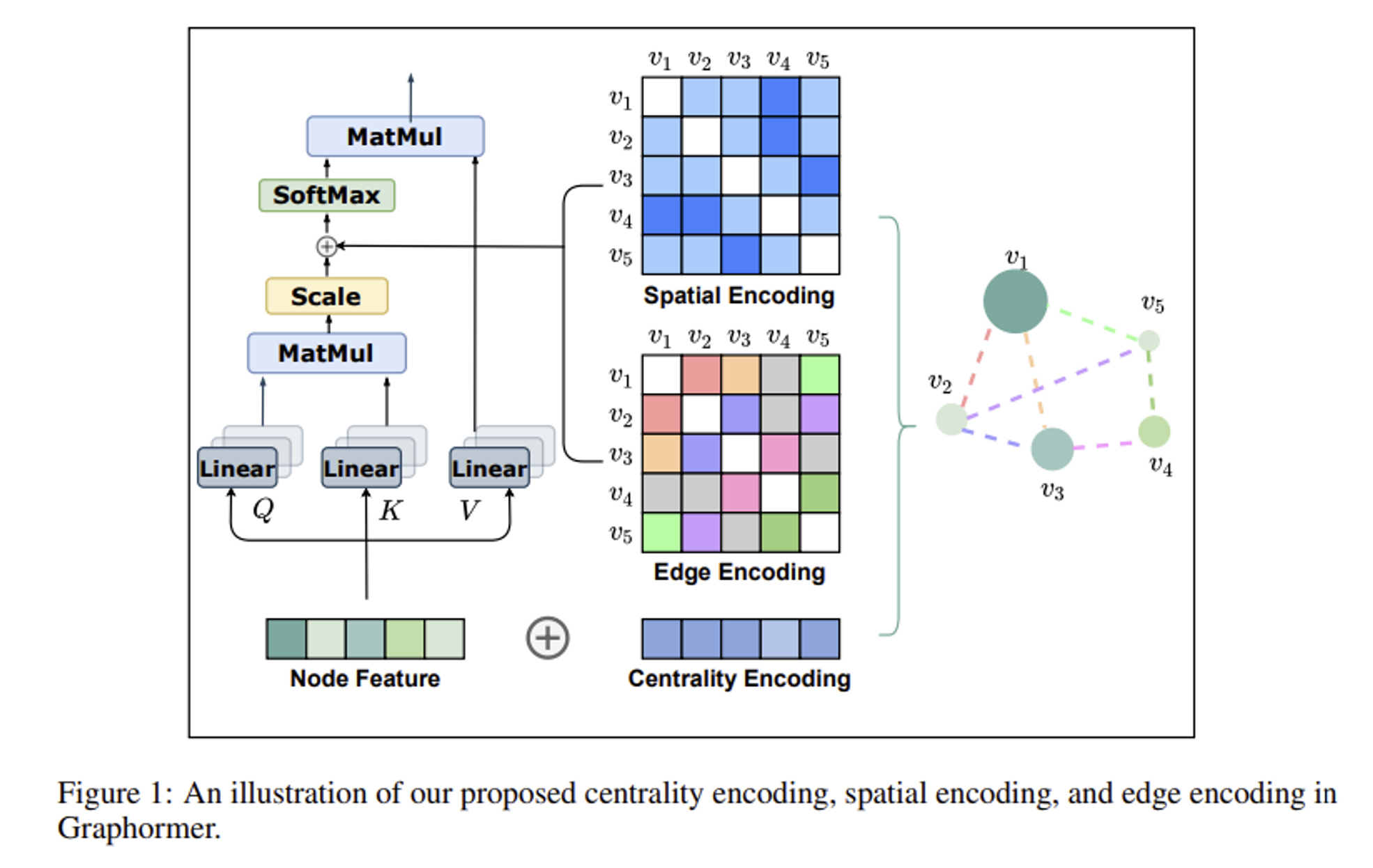
3.1.1 Centrality Encoding

Importance of node centrality

☹️ node embedding의 similarity를 기반으로 계산되는 기존 attention → node centrality의 특성을 반영하기 어려움

💡 Degree centrality

• indegree&outdegree → two real-valued embedding (learnable)

Apply centrality encoding to each node and simply add it to the node feature

$h_i^{ (0)} = x_i + z^ −_{ deg^−(vi)} + z^ +_{ deg^+(vi)}$

• undirected : 그냥 하나로 합침

💡 원래는 그냥 x(semantic embedding)로만 similarity를 구해서 attention을 구했었는데, learnable한 indegree, outdegree embedding을 더한걸 가지고 similarity를 바탕으로 attention을 계산하다 보니까 semantic correlation과 node importance모두 caputre할 수 있었다~!

3.1.2 Spatial Encoding

Transformer의 장점 중 global receptive field ← sequential하게가 아니라 한번에 문장내 모든 단어들에 대해 attention을 구해서 생기는 특성

⇒ byproduct problem : sequential data에 대해 순차적 process가 들어가지 않으니까 자연어 같은 애들은 positional encoding이 들어가야됨

• 그래프에서는 node가 sequence로 정렬되어있지 않음
• multi-dimensional spatial space, edge로 연결

💡 자연어에서는 그냥 positional encoding해주면 되는데 그래프는 sequential이 아니니까 다른 방법으로 structural information을 넣어준다 = Spatial encoding

⇒ Spatial Encoding

• Graph $G$에서 $v_i, v_j$사이 spatial relation을 측정하는 function $\phi(vi_i,v_j) : V \times V \rightarrow \R$
  • $\phi(vi_i,v_j)$는 노드들 사이 connectivity로 정의 = distance of shortest path(SPD)
  • 연결안된경우 -1
• 각 output value에 learnable scalar assign → self-attention 모듈의 bias term

• $A_{ij}$ : Query-Key matrix A의 $(i,j)$th element
  • $b_{\phi(v_i,v_j)}$ : $\phi(vi_i,v_j)$에 따라 assign된 learnable scalar, shared across all layers

💡 transformer에서 query를 바탕으로 다른 모든 key value들과 연산하고 그거를 softmax먹여서 score로 사용. score랑 value들 가중합해서 attention으로 사용. 여기 나와있는 A_ij는 score느낌인듯, 근데 degree centrality가 반영된 node embedding similarity만 구한게 아니라 거기에 bias term으로 distance of shortest path도 더해준 것!

장점

1. receptive field가 이웃 노드들로 제한되는 conventional GNN과 비교했을 때 transformer layer는 그래프 내의 모든 다른 노드들의 attend하며 global information을 제공
2. $b_{\phi(v_i,v_j)}$을 적용함으로써, transformer layer의 각 노드는 그래프의 구조적 정보(structural information)에 따라서 adaptively attend
   • ex. $b_{\phi(v_i,v_j)}$가 $\phi(vi_i,v_j)$에 따라 감소함수로 학습되었을 경우 → 모델은 가까운 노드를 더 attend하고, 멀리있는 노드는 상대적으로 덜 attend하게됨

3.1.3 Edge Encoding in the Attention

edge또한 구조적 특성을 가지는 경우

• ex. molecular graph, 원자쌍 사이 연결이 특정 type을 가지기도 함
• Traditional methods for edge encoding
  1. edge features가 연관된 nodes’ features에 더해짐
  2. 각 노드에 대해 연관된 edges’ features는 aggregation단계에서 node features와 함께 사용됨

⇒ 연관된 노드와의 edge 정보만 propagate → whole graph representation에 edge information을 활용하기에는 효율적인 방법이 아닌듯

• attention mechanism은 각 node pair $(v_i, v_j)$에 대해 correlation을 추정
  • 이때 두 노드를 연결하는 edge가 고려되어야함

⇒ 노드간 shortest path를 찾고, path를 따라 edge feature와 learnable embedding(Weight embedding)을 dot product하여 평균내는 방식

• spatial encoding처럼 bias term을 통해 추가됨

• $v_i$에서 $v_j$로 가는 shortest path $\text{SP}_{ij} = (e_1,e_2, ..., e_N)$
• $x_{e_n}$ : $\text{SP}_{ij}$ 에서 $n$번째 edge $e_n$의 feature
• $w_n^E \in \R^{d_E}$ : $n$번째 weight embedding(learnable embedding)
• $d_E$ : edge feature의 dimensionality

💡 spatial encoding할때도 shortest path를 learable scalar로 mapping해줬으니까 좀더 global한 단위의 edge feature도 마찬가의 방법으로 해준듯, 경로상 각 edge의 weight는 learnable하게 둬서 알아서 학습되도록

💡 노드간 거리말고 graph의 structural한 정보를 encoding한다면?
ex. 특정 구조의 subgraph -> 후속 논문으로 나온 Structure-Aware Transformer for Graph Representation Learning 의 베이스 아이디어!

3.2 Implementation Details of Graphormer

Graphormer Layer

Built upon classic Transformer encoder

• Multi-head self-attention(MHA)와 Feed-foward block(FFN)이전에 Layer Normalization(LN) 추가
  • On Layer Normalization in the Transformer Architecture
• FFN sub-layer에 대해서는 input, output, inner-layer를 $d$ dimension으로 통일

Special Node

Graph embedding을 만들기 위한 graph pooling function

• inspired by Neural Message Passing for Quantum Chemistry

[VNode]

• 그래프 내의 모든 노드와 각각 연결
• Aggregate-Combine 단계에서 그냥 일반 노드처럼 업데이트되고. 이를 통해 그래프 전체의 representation $h_G$가 이 Vnode의 representation이됨
• BERT에서 CLS 토큰을 sequence의 시작마다 두고 마지막에 문장 분류같은 sequence단위 downstream task에 쓰는거랑 마찬가지

☹️근데 그래프 내에 모든 노드랑 연결되어있으니까 shortest path가 항상 1! 근데 얘는 virtual connection이지, 실제연결이 아님

💡 reset all spatial encodings for $b_{ϕ([VNode],v_j)}$ and $b_{ϕ(v_i,[VNode])}$ to a distinct learnable scalar

• inspired by Rethinking Positional Encoding in Language Pre-training

3.3 How Powerful is Graphormer?

Fact 1. By choosing proper weights and distance function ϕ(Spatial encoding을위한 SPD를 scalar mapping해주는 function), the Graphormer layer can represent AGGREGATE and COMBINE steps of popular GNN models such as GIN, GCN, GraphSAGE.

1. self attention을 계산할 때 spatial encoding이 들어가서 노드의 neighbor set(SPD=1) 구분 가능 → softmax적용해서 이웃노드셋에 대한 평균 계산 가능
2. node의 degree를 위에서 구한 이웃노드셋에 대한 평균에다 곱해주면 sum으로 변환 가능
3. 멀티헤드 어텐션, FFN을 통해 노드 v, 그리고 이웃 노드셋의 representation은 따로 계산된 후에 나중에 합쳐짐 ← FFN은 vanilla transformer에서도 토큰단위로 따로 들어가는 거였음

😀 spatial encoding으로 WL test보다 더 expressive한 GNN(1WL test가 MPNN)

• appendixA에서 WL test로 구분하지 못하는 그래프를 grpahormer로 구분하는거랑 다른 GNN의 special case인거 증명

Connection between Self-attention and Virtual Node.

[VNode] Readout function처럼 전체그래프의 information을 aggregate하는 역할

☹️ can potentially lead to inadvertent over-smoothing of information propagation

Graph Warp Module: an Auxiliary Module for Boosting the Power of Graph Neural Networks in Molecular Graph Analysis

Fact 2. By choosing proper weights, every node representation of the output of a Graphormer layer without additional encodings can represent MEAN READOUT functions.

• self attention은 전체 노드를 attend ⇒ simulate graph-level READOUT operation to aggregate information from the whole graph
• Theoretically 뿐만아니라 empirically No over-smoothing problem ⇒ vnode추가로 graph readout 구현

4. Experiments

4.1 OGB Large-Scale Challenge

• graph-level prediction dataset

4.2 Graph Representation.

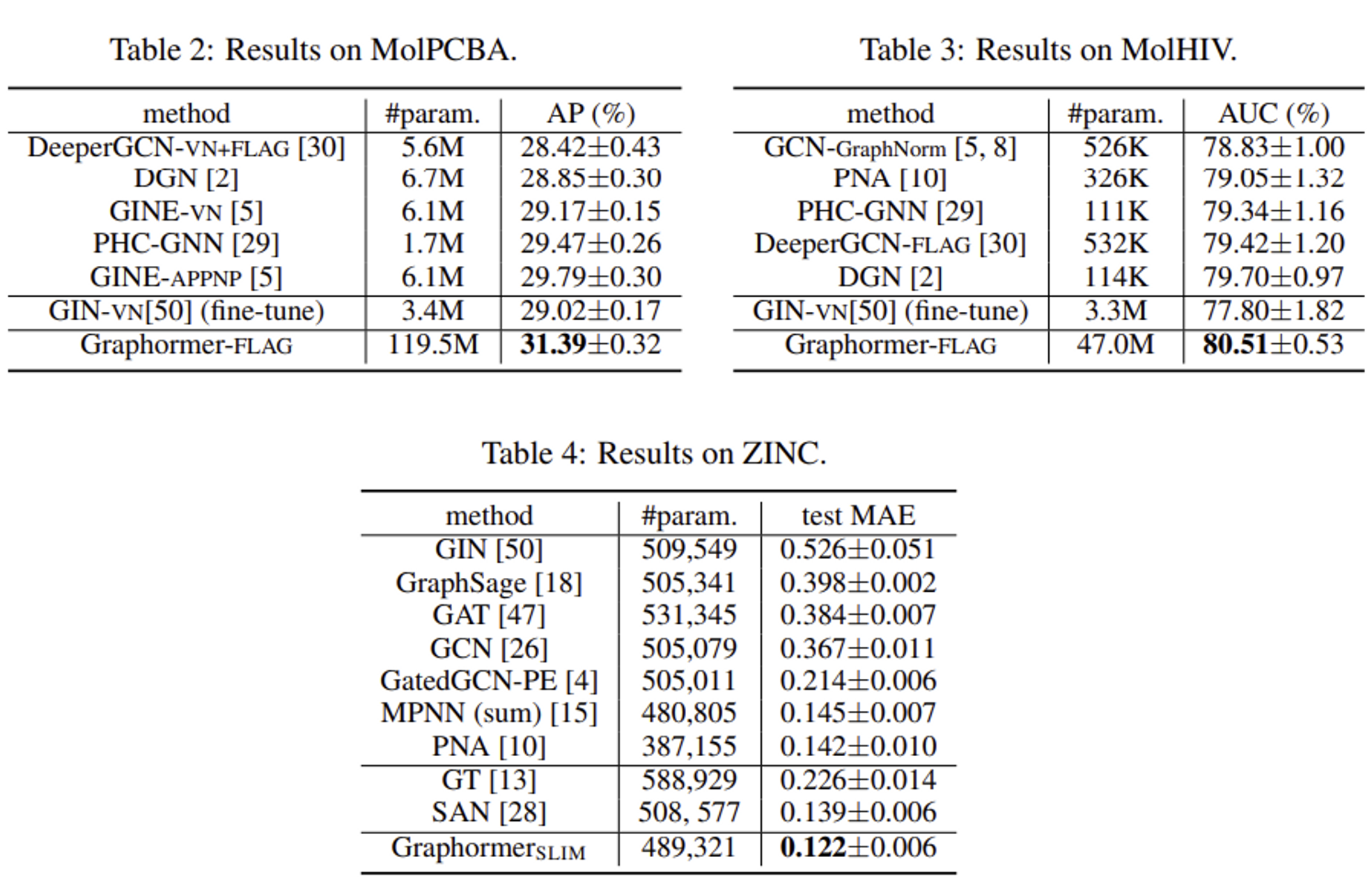
4.3 Ablation Studies

Node Relation Encoding

Positional encoding employed by previous Transfomer based-GNN

• Weisfeiler-LehmanPE (WL-PE) : Graph-Bert: Only Attention is Needed for Learning Graph Representations
• Laplacian PE : Laplacian Eigenmaps for dimensionality reduction and data representation

💡위의 Positional encoding방법론들을 적용한 것 보다 spatial encoding을 적용한게 더 잘됨

Centrality Encoding

💡없는거보다 있는게 더 잘됨 → transformer architecture로 그래프 데이터를 모델링하는데 centrality encoding을 적용하는게 필수!

Edge Encoding

traditional ways to encode edge

💡proposed edge encoding performs better

5. Related Work

5.1 Graph Transformer

5.2 Structural Encodings in GNNs

Path and Distance in GNNs

• Path-Augmented Graph Transformer Network : node features, edge features, one-hot feature of the distance and ring flag feature 들을 attention 계산 시 활용

Positional Encoding in Transformer on Graph

• Graph-Bert: Only Attention is Needed for Learning Graph Representations :
  • absolute WL-PE, intimacy based PE, hop based PE
• A Generalization of Transformer Networks to Graphs : Absolute Laplacian PE

Edge Feature

• Exploiting Edge Features in Graph Neural Networks : node similarity를 활용해 edge feature weight
• How powerful are graph neural networks? : project edge features to an embedding vector and multiply it by attention coef, and send the result to an additional FFN sub-layer to produce edge representations

6. Conclusion

• graph structural encodings
  • Centrality Encoding
  • Centrality Encoding
  • Edge Encoding
• works well on wide range of popular benchmark datasets
• challange
  - quadratic complexity of the self-attention module restricts Graphormer’s application on large graphs

  💡 GAT와 Transformer : GAT에서는 node embedding의 semantic한 similarity를 기반으로 attention을 구했다면, Transfomer는 여기에 degree centrality, spatial encoding, edge feature를 추가한 attention을 계산. 이 세가지를 attention을 구하는데 집어넣는 과정에서 각각의 representation에 대해 learnable한 function들을 도입하여 학습 과정에서 그 weight를 학습하게되는 방식.
  Attention을 사용했을 때 장점은 노드의 이웃여부와 관계없이 모든 노드를 attend할 수 있다는 것 ⇒ global receptive field
  🤷 그럼 기존 MPNN 레이어를 쌓아서 hop을 늘리면 되는거 아니냐 라고하면?
  ⇒ 그랬을때는 oversmoothing problem(increasing the number of GNN layers, the features tend to converge to the same value)이 있음
  💡 Transfomer가 CNN, LSTM, GNN, GCN 같은 애들보다 잘하는건 적은 inductive bias때문이라고 할 수 있을거 같다. 기존 모델들은 들어가는 데이터의 특성(이미지의 경우 locality, 시계열의 경우 sequential)을 살린 모델 구조라서 inductive bias가 세게 걸려있다고 할 수 있다.
  반면 Transformer는 그런거 없이 개별토큰이 모든 intput에 대해 attend하기도 하고, locality나 sequentiality같은 것들은 positional encoding으로 상대적으로 약하게 걸려있다고 할 수 있다. ⇒ inductive bias가 적게 걸려있어서 NN이 학습할 수 있는게 더 많았다! ⇒ 데이터가 많을때 더 잘 작동한다!
  🤷 근데 그럼 데이터가 적은데 transformer를 사용하려면?
  ⇒ 추가적인 inductive bias를 줄 수 있는 방법에 대해 고민해봐야할 듯