✔ 목차
- BFS
- BFS 구현 - Java
- DFS
- DFS 구현 - Java
- 시간복잡도
🔎 BFS
너비 우선 탐색 (BFS, Breadth-First Search)
- 시작 정점 방문 후 가까운 정점 우선 방문
- 넓게 탐색하는 방법
- 두 노드 사이 최단 거리, 최단 경로 구할 때 자주 사용
- 장점
- 단점
💻 BFS 구현 - Java
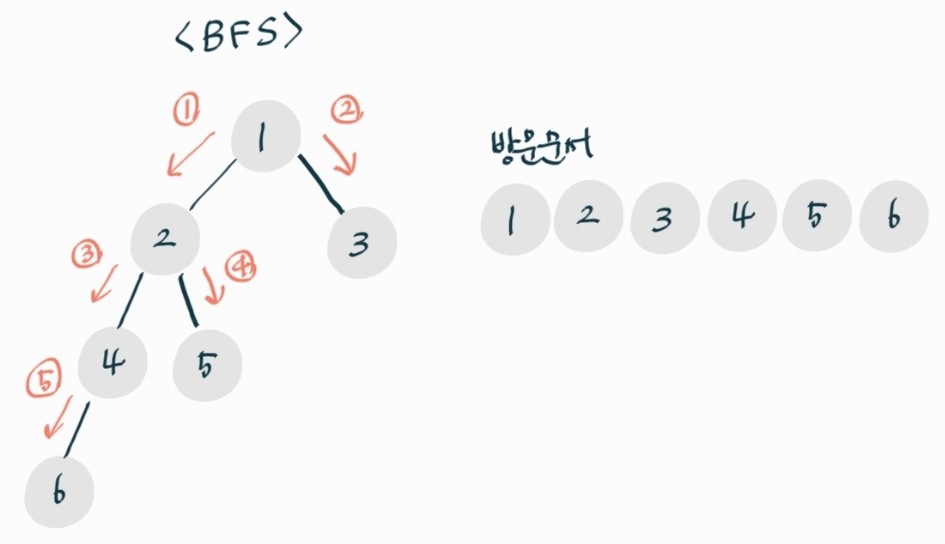
- 정점 v 방문한다.
- 정점 v에 인접한 정점 중 방문하지 않은 정점을 차례로 방문하면서 큐에 넣는다.
- 인접한 정점 모두 방문했다면 큐에서 dqueue하여 받은 값 정점 v로 설정하고 2를 반복한다.
- 큐가 공백이라면 탐색 완료한 것이다.
static boolean[] visit;
static LinkedList<Integer>[] graph;
static int[][] graph;
public static void bfs(int v) {
Queue<Integer> queue = new LinkedList<>();
queue.add(v);
visit[v] = true;
while(!queue.isEmpty()) {
int temp = queue.poll();
System.out.println(temp);
for(int nextV : graph[temp]) {
if(!visit[nextV]) {
queue.add(nextV);
visit[nextV] = true;
}
}
}
}
출력
1 2 3 4 5 6
🔎 DFS
깊이 우선 탐색 (DFS, Dreadth-First Search)
- 시작 정점 방문 후 다음 분기로 넘어가기 전 해당 분기 완벽하게 탐색
- 트리에서 보면 노드 방문 후 자식 노드 우선 방문
- 깊게 탐색하는 방법
- 장점
- 단점
- 찾은 해가 최적 해 아닐 가능성 있음
- 최악의 경우 해 찾는데 가장 오랜 시간 걸림
💻 DFS 구현 - Java
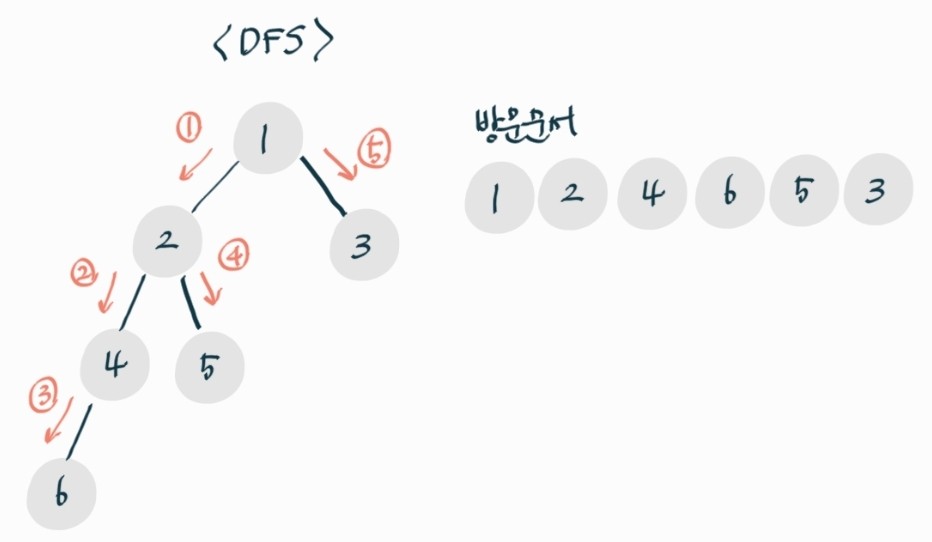
- 정점 v 방문한다.
- 정점 v에서 인접한 정점 중에 방문하지 않은 정점 w가 있다면 w를 v로 하여 1부터 반복한다(재귀함수 호출).
- 인접한 정점 모두 방문했다면 스택에서 정점을 꺼내 위를 반복한다.
static boolean[] visit;
static LinkedList<Integer>[] graph;
static int[][] graph;
public static void dfs(int v) {
visit[v] = true;
System.out.println(v);
for(int nextV : graph[v]) {
if(!visit[nextV]) dfs(nextV);
}
}
출력
1 2 4 6 5 3
⏰ 시간복잡도
- BFS DFS 둘의 시간복잡도는 동일하며, 그래프 구현에 따라 시간 복잡가 달라짐
- 연결 리스트로 구현한 그래프: O(n+m)
- 행렬로 구현한 그래프: O(n^2)
| 구현 | 시간복잡도 |
|---|
| 연결리스트 | O(n+m) |
| 행렬 | O(n^2) |



