[알고리즘/Java] 동적계획법

✔ 목차

1. 동적계획법(Dynamic Programming)이란?
2. 동적계획법 예시 - 피보나치 수열
3. Bottom-up과 Top-down

---

🔎 동적계획법이란?

동적계획법을 통해 불필요한 계산을 줄여 효율적으로 최적해를 구할 수 있다.

동적계획법(Dynamic Programming)

• 큰 문제를 작은 문제로 나누어서 해결하는 방법
• 큰 문제 해결 위해 작은 문제를 활용 -> 점화식 만들 수 있음
• 분할과 정복이랑 다르게 이전 연산 기록하여 재사용
  
  

메모이제이션(Memoization)

• 작은 문제 연산 값 기록하고 필요한 순간에 다시 연산하지 않고 기록했던 값 사용
• 중복 계산 줄여줌
  
  

---

💻 동적계획법 예시 - 피보나치 수열

피보나치 수열은 첫 번째, 두 번째 항이 1이고 나머지 항은 전 항과 전전 항의 값을 더한 값이다.

1 1 2 3 5 8 13 21 34 55 89 144

1. 피보나치 수열 구하기

다음은 재귀를 통해 구현한 n번째 피보나치 수열을 구하는 함수이다.

	public static int F(int n) {
		if (n <= 2)
			return 1;
		else
			return F(n - 1) + F(n - 2);
	}

이 코드의 단점은 불필요한 중복 연산이 많아진다. 다음은 F(6)을 구하는 방식이다.

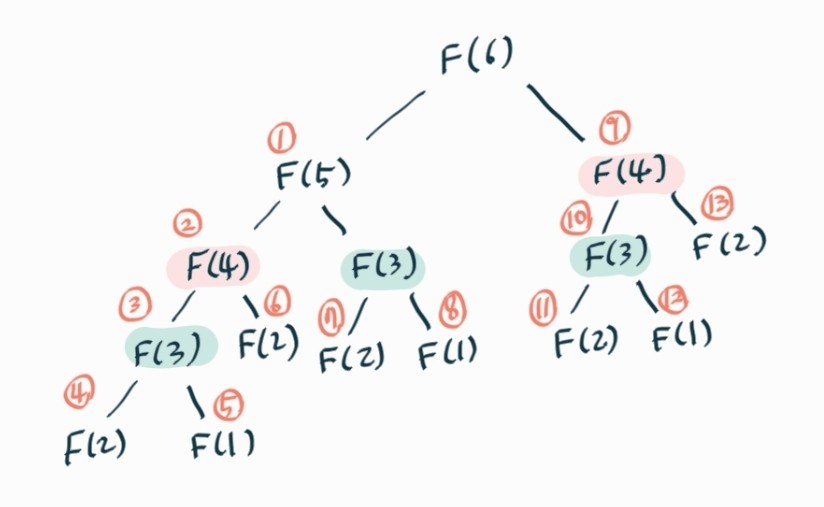
사진에서 F(3) 연산이 3번, F(4) 연산이 2번이 된 것을 볼 수 있다. 이처럼 같은 연산을 반복하는 것을 볼 수 있다.

2. 동적 계획법을 통한 피보나치 수열 구하기

이미 했던 연산을 반복하지 않기 위해서 연산 값을 저장하는 배열 Fibo을 생성한다. Fibo[n]에 값이 있다면 활용하고, 없다면 계산하여 저장해준다.

	//연산 결과 저장 배열
	static int[] fibo = new int[100];
	
	public static int F(int n) {
		if (n <= 2)
			return 1;
		if (fibo[n] == 0)
			fibo[n] = F(n - 1) + F(n - 2);
		return fibo[n];
	}

---

🔎 Bottom-up과 Top-down

Top-down

• 큰 문제 해결하는데 작은 문제가 해결되지 않았다면 그 때 작은 문제 해결하는 방법
• 주로 재귀함수 통해서 구현
• 위에서 예시로 든 피보나치 수열 구하기가 이에 해당됨

	static int[] fibo = new int[100];
	
	public static int F(int n) {
		if (n <= 2)
			return 1;
        //배열에 연산 값이 없으면 계산하여 저장해주기
		if (fibo[n] == 0) 
			fibo[n] = F(n - 1) + F(n - 2);
		return fibo[n];
	}

Bottom-up

• 작은 문제를 해결하면서 큰 문제를 해결하는 방법
• 주로 반복문으로 구현

	static int[] fibo = new int[100];

	public static int F(int n) {
		fibo[0] = 0;
		fibo[1] = 1;
		for (int i = 2; i <= n; i++) {
			fibo[i] = fibo[i - 1] + fibo[i - 2];
		}
		return fibo[n];
	}