✔ 목차
- 플로이드-와샬 알고리즘이란?
- 플로이드-와샬 알고리즘 과정
- 플로이드-와샬 알고리즘 구현 - Java
🔎 플로이드-와샬 알고리즘이란?
그래프 최단 거리 구하는 알고리즘
1. 다익스트라(Dijkstra)
2. 벨만-포드(Bellman-Frod)
3. 플로이드-와샬(Floyd-Wrasahll)
플로이드-와샬(Folyd-Warshall) 알고리즘
- 그래프의 최단 경로 구하는 알고리즘 하나
- 모든 정점에서 모든 정점까지 최단 거리를 구함
- 음수 사이클이 없어야함 (음수 가중치는 허용)
- 그래프 비용 인접 행렬로 표현되어 있다고 가정
- 시간 복잡도
O(n^3) - 동적 계획법 이용
🔎 플로이드-와샬 알고리즘 과정
경유지 k, 출발 정점 i, 도착 정점을 j라고 하자. 그래프는 graph라는 이중 배열에 저장되어있다.
graph[i][j]는 지금까지 i에서 j까지 가는 최단 거리이다.
graph[i][k] + graph[k][j]는 i에서 j까지 가는데 k를 거쳐서 가는 거리이다.
만약, graph[i][j] > graph[i][k] + graph[k][j]면 i부터 j까지 가는데 k를 거쳐서 가는 것이 더 최단 거리이다. 따라서 graph[i][j]는 graph[i][k] + graph[k][j]로 갱신해준다.
graph[i][j] = min(graph[i][j], graph[i][k] + graph[k][j])
예시
다음과 같은 가중치 방향 그래프가 있다. 이중 배열로 그래프를 표현했으며 이 이중배열을 graph라 하자.

1) 1번 정점를 경유하여 가는 경우를 살필 것이다. 1번 정점에서 출발하는 경우와 도착하는 경우를 빼고 나머지 정점에 대해 살펴본다.
-
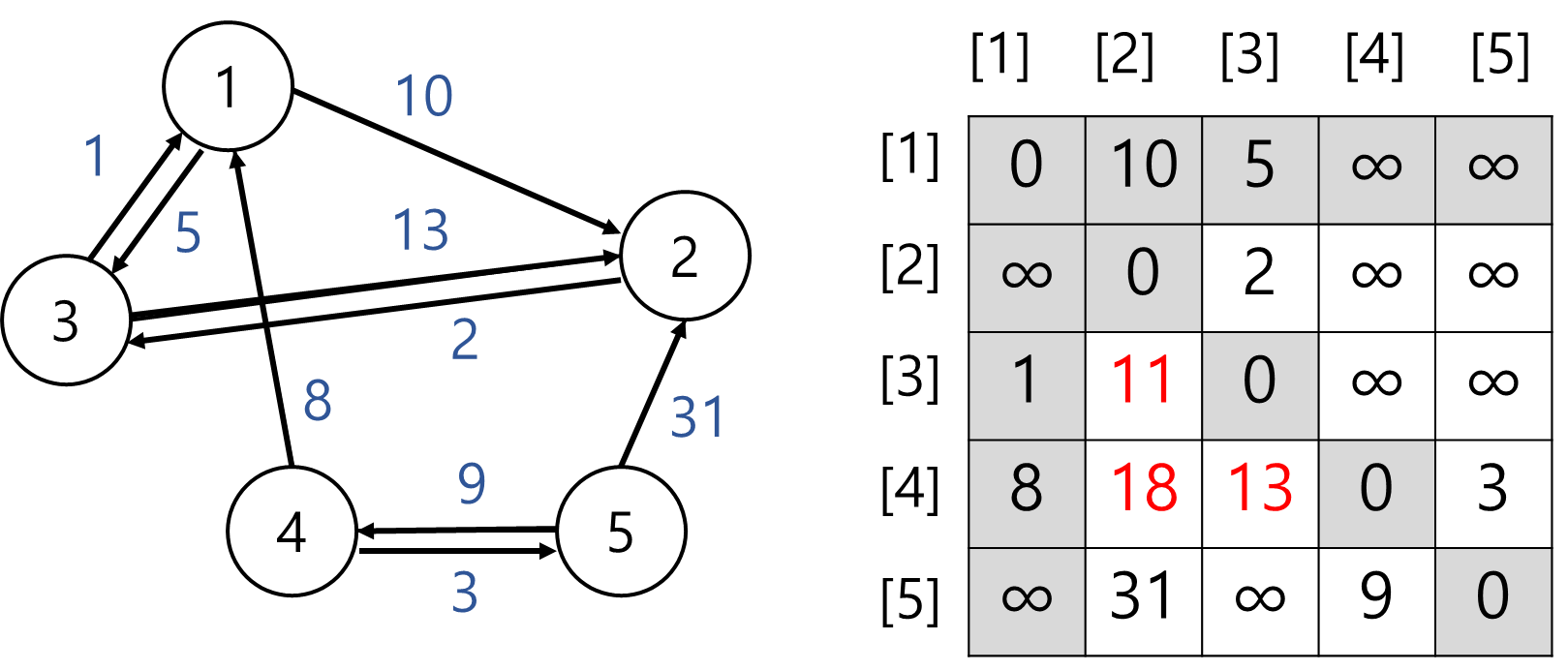
graph[3][2]= 11로 값 변경
①graph[3][2]= 13이다.
②graph[3][1]+graph[1][2]= 1 + 10 = 11이다.
① > ② 이므로graph[3][2]값을 11로 변경해준다. -
graph[4][2]= 11로 값 변경
①graph[4][2]= 무한이다.
②graph[4][1]+graph[1][2]= 8 + 10 = 11이다.
4에서 1을 경유하고 2로 갈 수 있으므로graph[4][2]값을 18로 변경해준다. -
graph[4][3]= 13로 값 변경
①graph[4][3]= 무한이다.
②graph[4][1]+graph[1][3]= 8 + 5 = 13이다.
4에서 1을 경유하고 3으로 갈 수 있으므로graph[4][3]값을 13으로 변경해준다.
2) 2번 정점를 경유하고 가는 경우를 살펴본다.

-
graph[5][3]= 13로 값 변경
①graph[5][3]= 무한이다.
②graph[5][2]+graph[2][3]= 31 + 2 = 33이다.
5에서 2을 경유하고 3으로 갈 수 있으므로graph[5][3]값을 33으로 변경해준다. -
graph[1][3]값 변경 없음
①graph[1][3]= 5이다.
②graph[1][2]+graph[2][3]= 10 + 2 = 12이다.
① < ② 이므로graph[1][3]값은 그대로이다.
이런 방식으로 정점 5까지 반복해준다.
3) 정점 3 경유
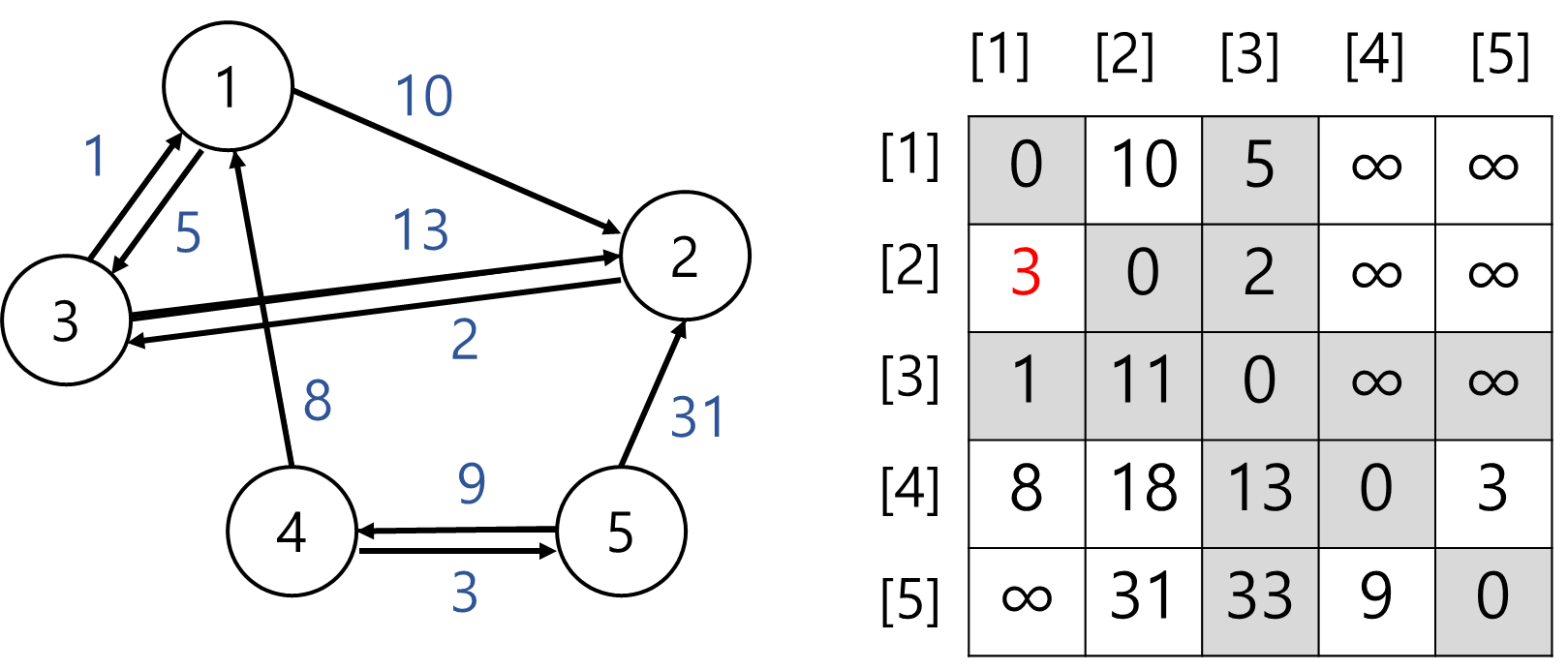
4) 정점 4 경유
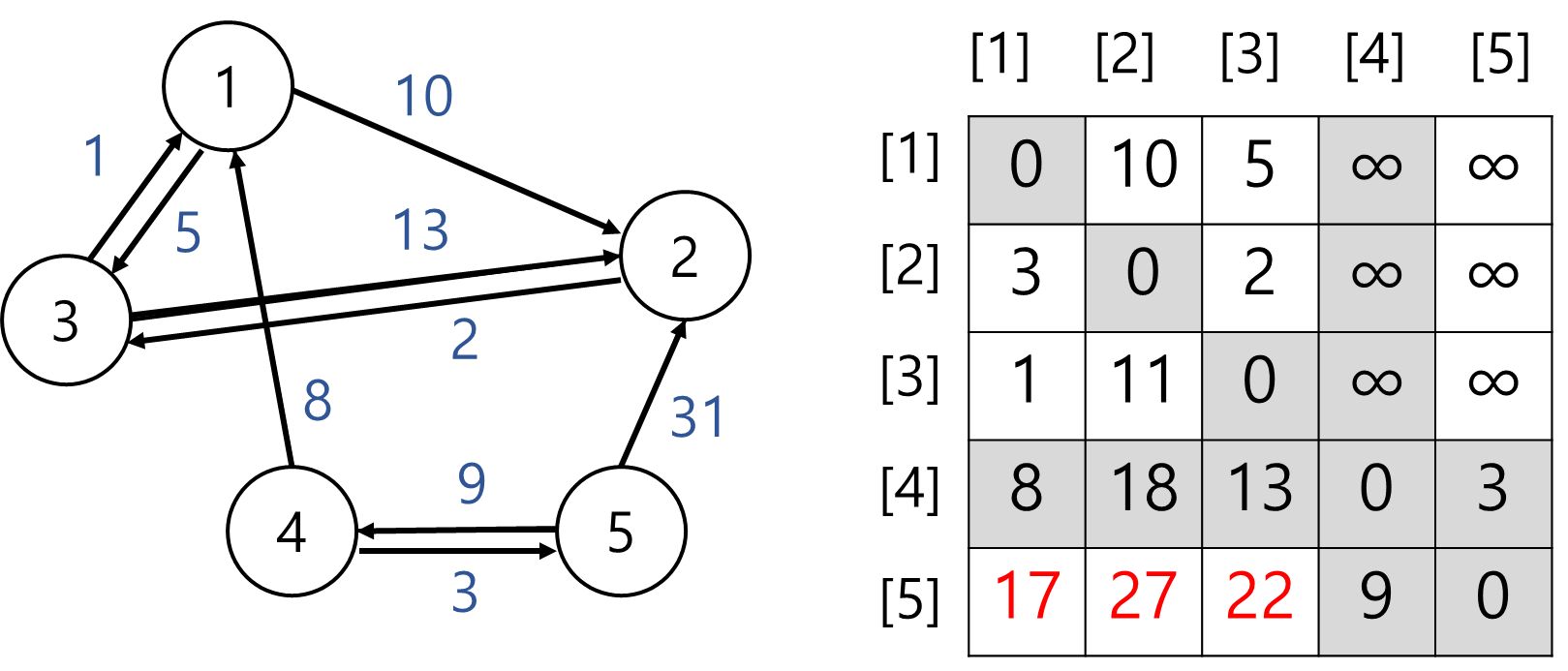
5) 정점 5 경유
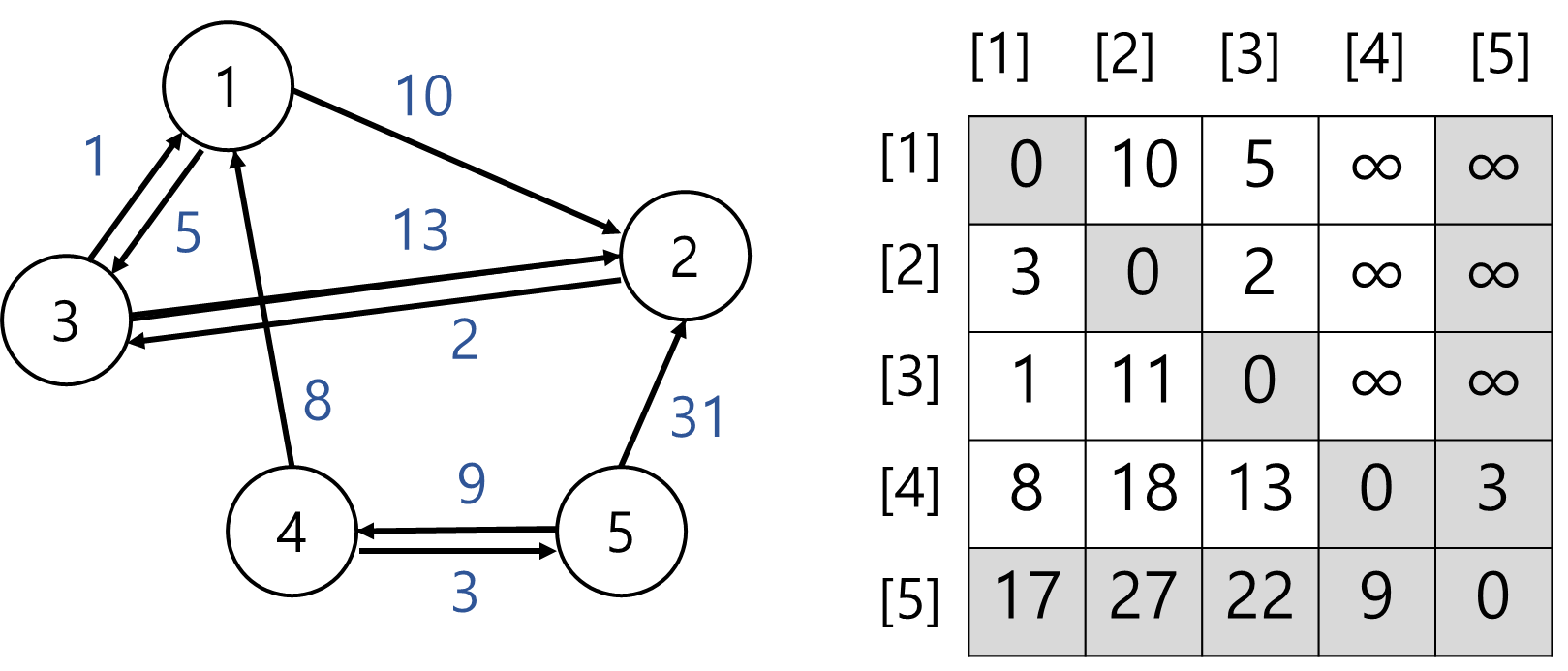
최종) 플로이드-와샬 알고릴즘 수행

💻 플로이드-와샬 알고리즘 구현 - Java
플로이드 알고리즘
//이중 배열에 저장된 그래프, 정점의 개수 넘겨줌
public static void floyd(int[][] graph, int n) {
// 경유지
for (int k = 1; k <= n; k++) {
// 출발지
for (int i = 1; i <= n; i++) {
//도착지
for (int j = 1; j <= n; j++) {
graph[i][j] = Math.min(graph[i][j], graph[i][k]+graph[k][j]);
}
}
}
}전체 코드
public class Main {
static final int INF = 1000000000;
public static void floyd(int[][] graph, int n) {
// 경유지
for (int k = 1; k <= n; k++) {
// 출발지
for (int i = 1; i <= n; i++) {
//도착지
for (int j = 1; j <= n; j++) {
graph[i][j] = Math.min(graph[i][j], graph[i][k]+graph[k][j]);
}
}
}
//출력
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if(graph[i][j] == INF) System.out.print(0+" ");
else System.out.print(graph[i][j]+" ");
}
System.out.println();
}
}
public static void main(String[] args) throws IOException {
//그래프 입력 받기
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
// 정점의 개수, 간선의 개수
int n = Integer.parseInt(bf.readLine());
int m = Integer.parseInt(bf.readLine());
int[][] graph = new int[n + 1][n + 1];
for (int i = 0; i < graph.length; i++) {
for (int j = 0; j < graph.length; j++) {
if(i == j) continue;
graph[i][j] = INF;
}
}
StringTokenizer st;
for (int i = 0; i < m; i++) {
st = new StringTokenizer(bf.readLine());
int v = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
graph[v][w] = cost;
}
//플로이드 알고리즘 수행
floyd(graph, n);
}
}입력
5
9
1 2 10
1 3 5
2 3 2
3 1 1
3 2 13
4 1 8
4 5 3
5 4 9
5 2 31
출력 결과
0 10 5 0 0
3 0 2 0 0
1 11 0 0 0
8 18 13 0 3
17 27 22 9 0 
