[알고리즘/Java] 정렬

✔ 목차

0. 정렬 알고리즘
1. 삽입 정렬
2. 선택 정렬
3. 거품 정렬
4. 퀵 정렬
5. 합병 정렬
6. 힙 정렬
7. 이진 탐색 트리를 이용한 정렬
8. 시간 복잡도 정리

---

🔎 정렬 알고리즘

정렬은 대개 분할 정복법으로 이뤄진다. 나누는 방법에 따라 시간 복잡도가 달라진다. 또한 정렬은 트리를 이용하여 할 수 있다.

분할 정복법으로 구현한 정렬

• 1개와 n-1개로 나눔 -> O(n^2) 시간
  • 삽입 정렬
  • 선택 정렬
  • 거품정렬
• n/2개로 나눔 -> O(n^2)혹은 O(nlog n)시간
  • 퀵 정렬
  • 합병 정렬

트리를 이용한 정렬

• 힙 정렬
• 이진 탐색 트리를 이용한 정렬

---

🔎 삽입 정렬

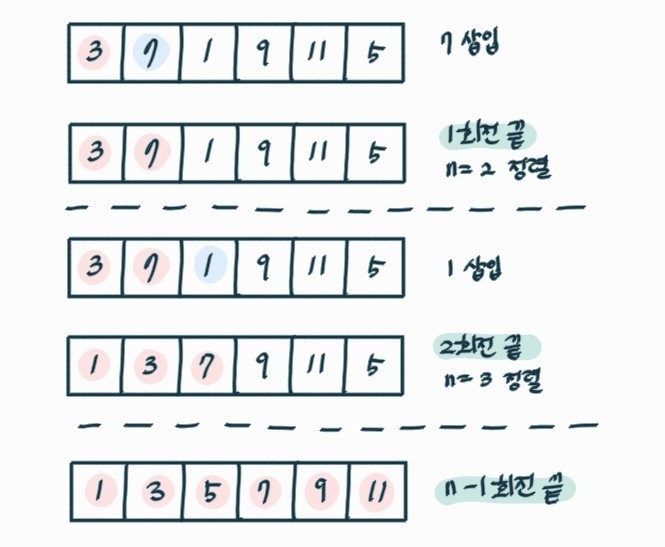
정렬된 원소의 개수 키운다. n개 정렬 위해서 n-1개 정렬되어 있어야 한다.

삽입 정렬 로직
1) 첫 번째 인덱스 정렬 됐다고 가정한다.
2) 다음 인덱스를 지금껏 정렬된 배열에 추가하여 정렬한다. -> 정렬된 인덱스 하나 증가
3) n개까지 반복한다.

• 시간복잡도

  T(n) = T(n-1) + O(n)
  T(n) <= T(n-1) + cn = O(n^2) (*c는 상수)

---

🔎 선택 정렬

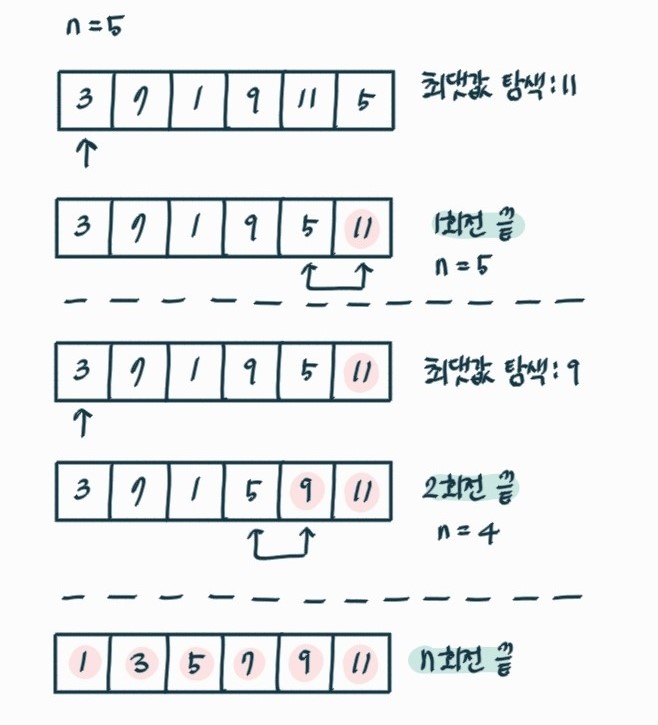
제일 큰 원소 맨 뒤로 보낸다. 이를 제외한 나머지 n-1 배열 다시 정렬한다.

선택 정렬 로직
1) 배열 중 가장 큰 원소 탐색한다.
2) 고른 원소 맨 마지막 인덱스로 보낸다.
3) 맨 마지막 인덱스는 정렬되었으므로 이를 뺀 n-1 원소로 다시 반복한다.

• 시간복잡도

  T(n) = T(n-1) + O(n) = O(n^2)

---

🔎 거품 정렬

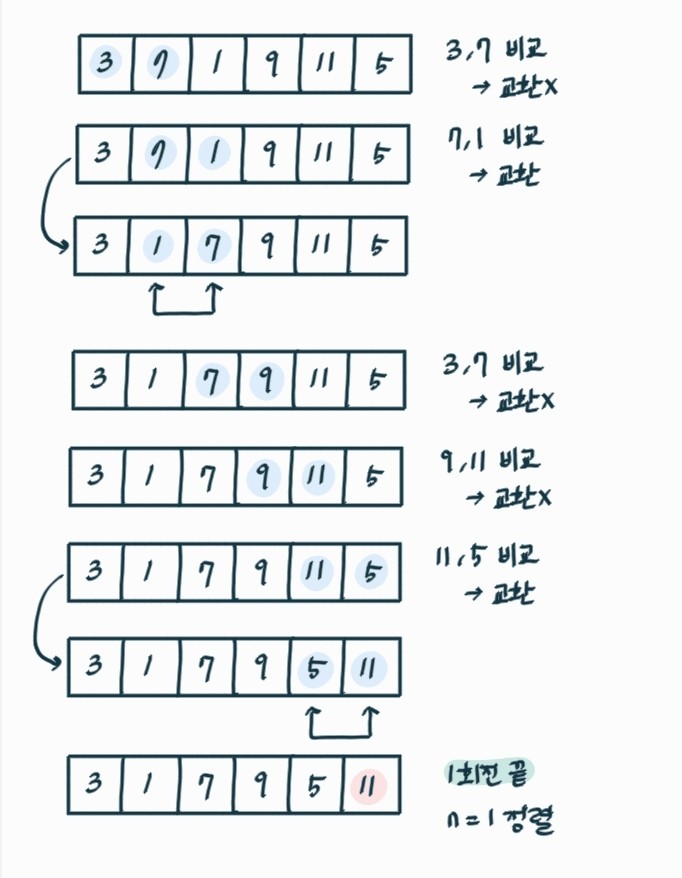
버블 정렬이라고도 한다. 인접 원소 비교하여 크면 오른쪽, 작으면 왼쪽으로 보낸다. 1회전 끝나면 제일 큰 원소 오른쪽으로 간다.

거품 정렬 로직
1) 첫 번째 인덱스와 두 번째 인덱스 비교한다.
2-1) 첫 번째 인덱스 값이 더 크면 두 값을 바꾸고 다음 인덱스와 비교한다.
2-2) 첫 번째 인덱스 값이 더 작으면 두 번째 인덱스와 다음 인덱스와 비교한다.
3) 맨 마지막 인덱스까지 비교하면 1회전이다.
4) 맨 마지막 인덱스는 정렬되었으므로 이를 뺀 n-1 원소로 다시 반복한다.

• 시간복잡도

  T(n) = T(n-1) + O(n) = O(n^2)

---

🔎 퀵 정렬

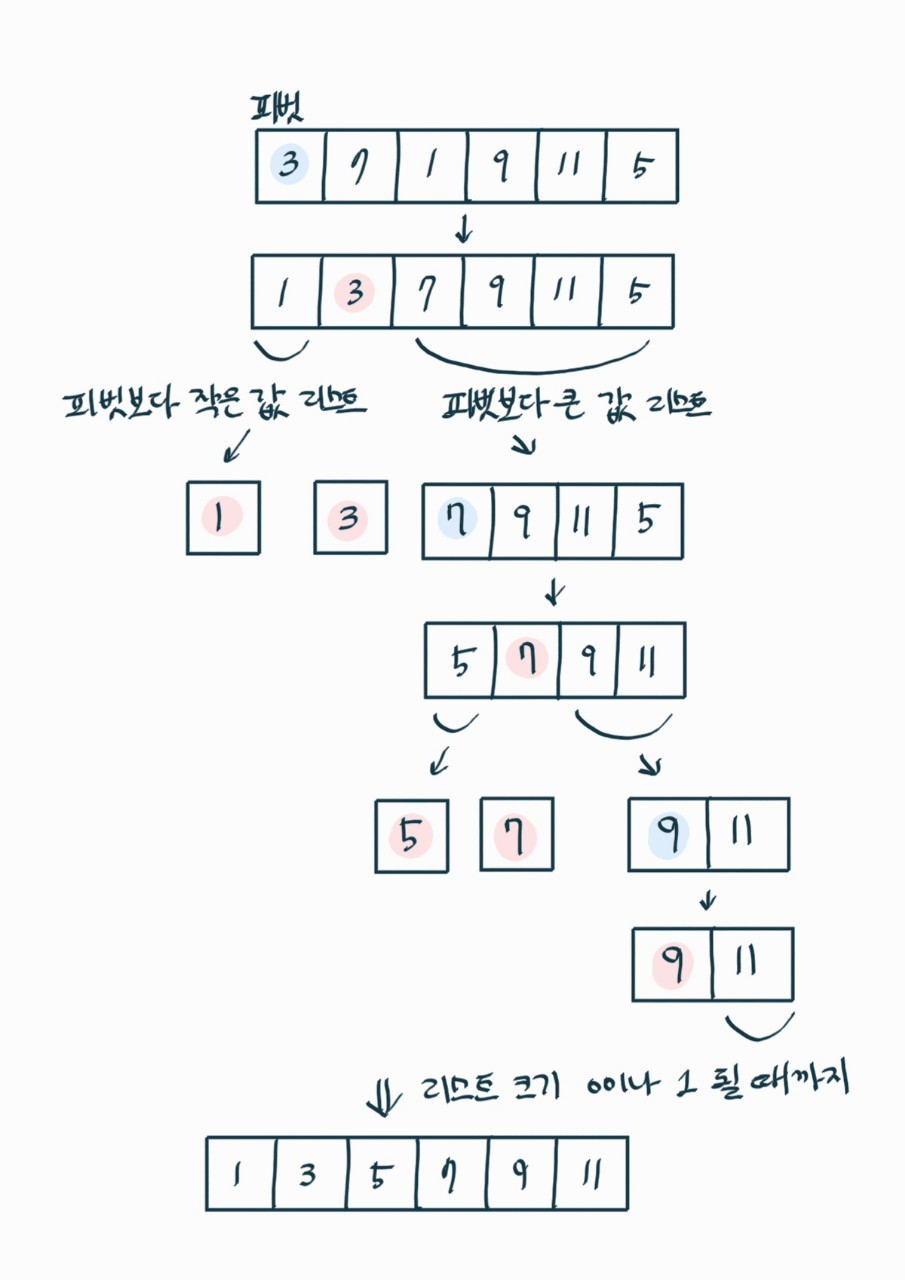
리스트 임의의 원소 피벗 기준으로 큰 원소, 작은 원소 나누어서 정렬한다.

퀵 정렬 로직
1) 리스트에서 원소 하나를 골라 피벗(pivot)이라 한다.
2) 피벗과 n-1 원소를 각 비교하여 피벗보다 작은 원소 리스트와 큰 원소 리스트로 분할한다.
3) 분할된 리스트별로 리스트 크기가 1이나 0이 될 때까지 위를 반복한다.

• 시간복잡도

  • 피벗이 중앙값인 최선의 경우: 2/n개씩 나뉨
    T(n) <= 2ⅹT(n/2) + cn = O(nlog n)
  • 피벗이 최솟값/최댓값인 최악의 경우: 하나와 n-1개로 나뉨
    T(n) <= T(n-1) + cn = O(n^2)

퀵 정렬은 다른 정렬 알고리즘보다 빠르다고 알려져 있다.

---

🔎 합병 정렬

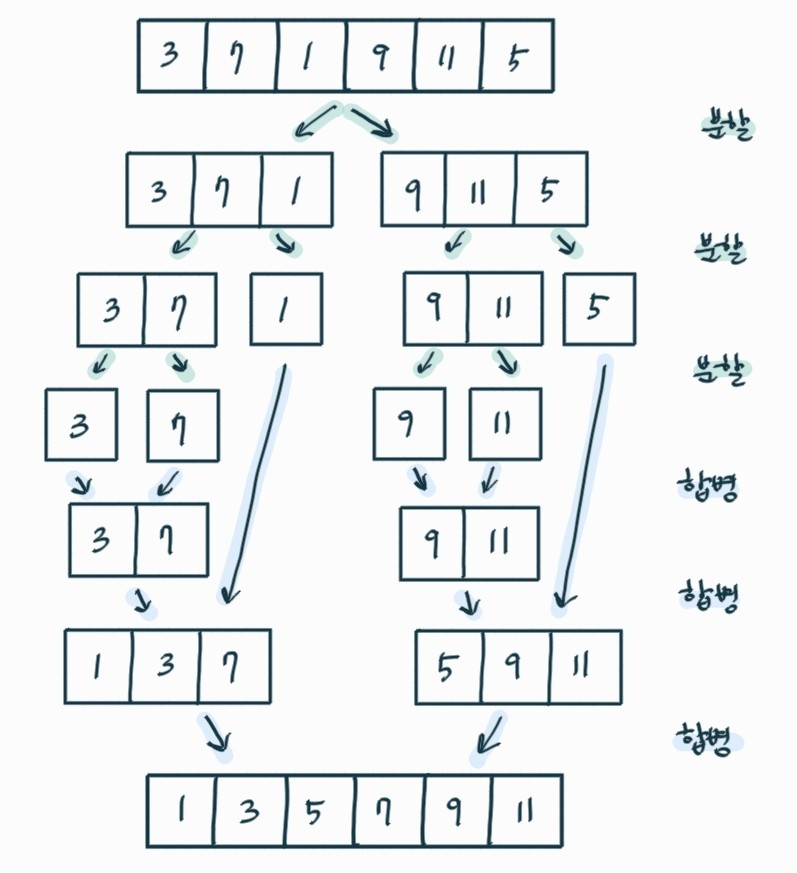
리스트를 나누어 길이가 0또는 1이 될 때까지 반복한다. 이후 합병을 통해 정렬한다.

합병 정렬 로직
1) 리스트 길이가 0 또는 1이면 정렬된 것으로 간주한다.
2) 리스트 길이가 2 이상이면 리스트 절반으로 잘라 부분 리스트로 나눈다.
3) 모든 부분 리스트의 길이가 0 또는 1이 될 때까지 반복한다.
4) 리스트 나눈 역순으로 리스트 합병을 하며 정렬한다.

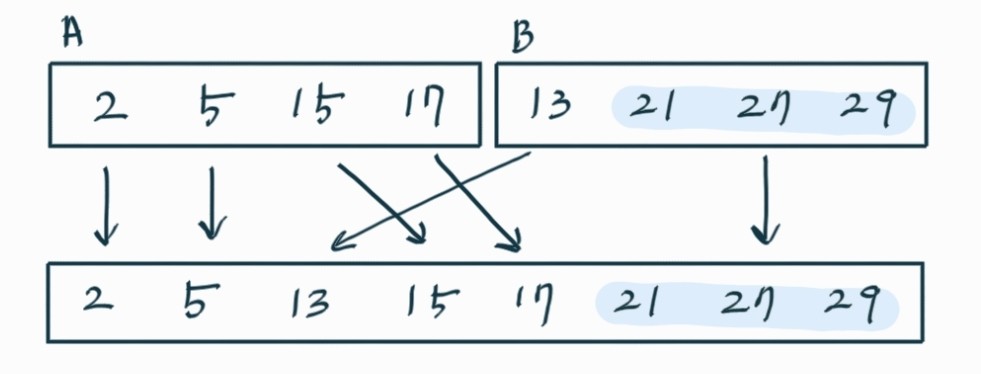
합병 방식
A리스트와 B리스트 합병한다고 가정
1) A리스트의 최솟값과 B리스트의 최솟값 비교
2) A리스트 최솟값이 더 작다면 새 리스트에 추가하고 다음 인덱스 값과 B리스트 최솟값 비교
3) A리스트 또는 B리스트의 모든 인덱스 비교했다면 나머지 원소들 리스트에 추가

• 시간복잡도

  • 리스트 분할 시 시간: O(1)
  • 리스트 합병 시 시간:
    리스트 합병 시 원소 비교 횟수 ⅹ 합병 횟수
    • 리스트 합병 시 원소 비교 횟수: 최악의 경우 두 리스트의 원소 개수합 -> O(n)
    • 합병 횟수: 분할된 리스트 층수 -> O(log n)
      => 합병은 분할의 역순으로 일어나므로 분할된 리스트 층수만큼 합병한다.
      => 분할 시 각 층마다 리스트를 1/2로 나누므로 k층에는 리스트 2^k가 생긴다. k층에서 크기 n인 리스트를 크기 1인 리스트 n개로 만들었다면 n = 2^k가 되므로 k = log_2 n이다.
      => 분할된 리스트 층수는 log_2 n이다.
  O(n) ⅹ O(log n) = O(nlog n)

---

🔎 힙 정렬

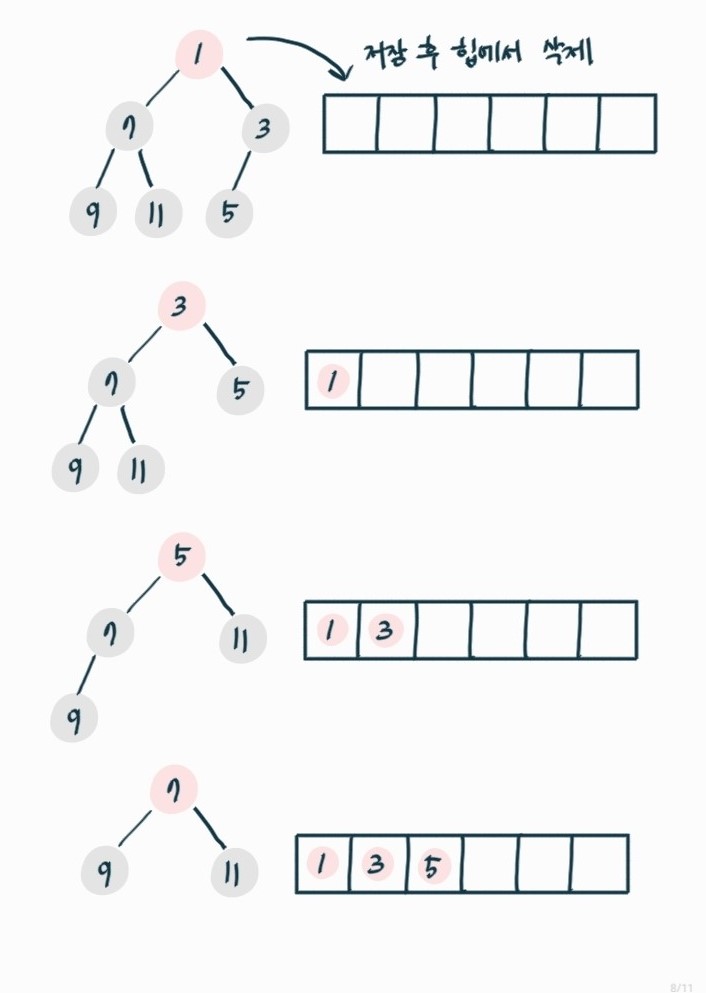
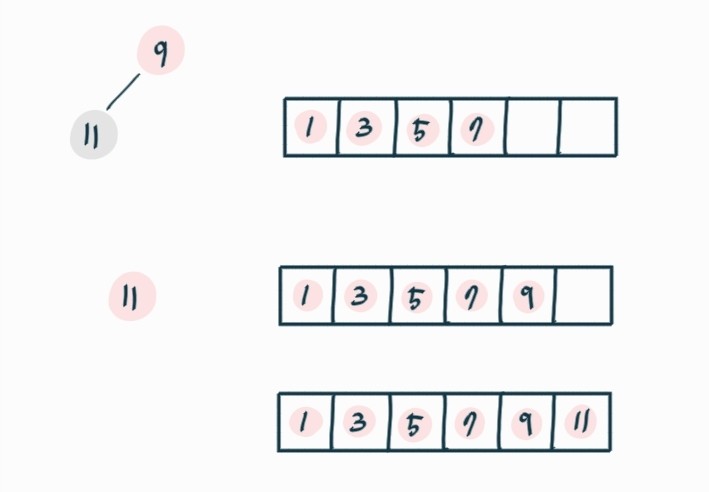
힙에서 최댓값 저장 후 삭제를 반복한다.

힙 정렬 로직
1) 최대 힙의 첫 번째 원소는 가장 큰 값이다. 이를 배열에 저장한다.
2) 최소 힙의 첫 번째 원소 삭제한다.
3) 이를 원소의 개수만큼 반복한다.

• 시간복잡도

  원소 힙 삽입시간 + 원소별 최댓값 저장 후 삭제
  n ⅹ O(log n) + cn = O(nlog n)

힙 알고리즘 자세히 알아보기

---

🔎 이진 탐색 트리를 이용한 정렬

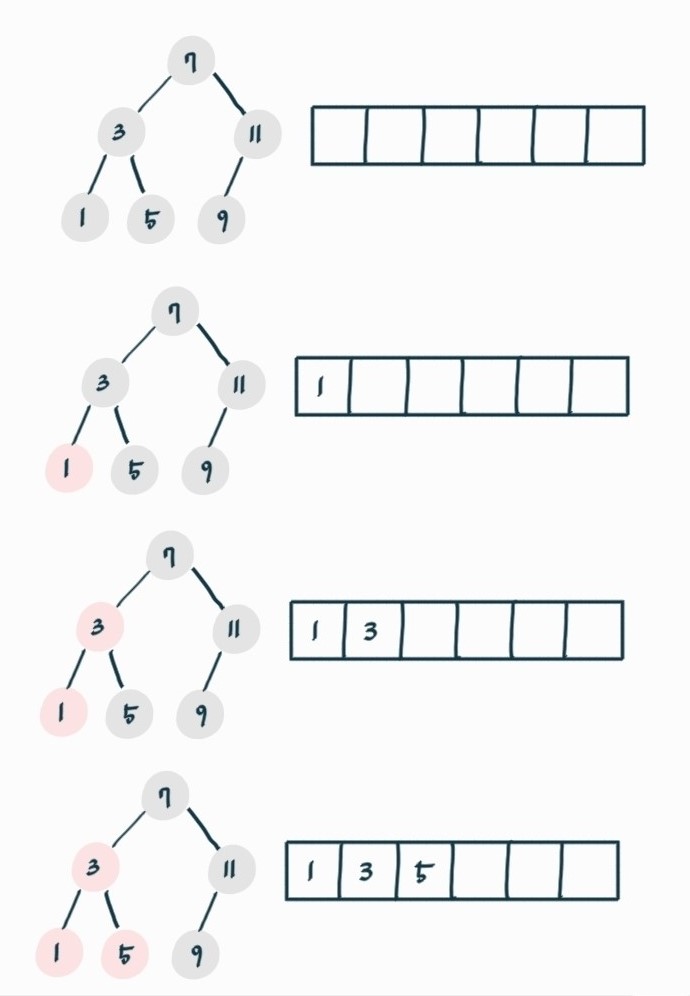
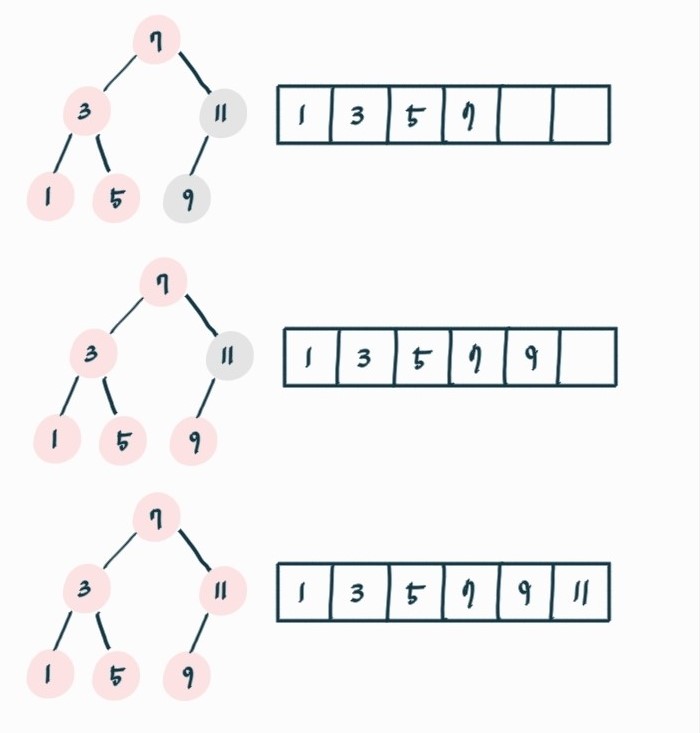
이진 탐색 트리에서 중위 순회하면서 원소를 저장한다.

이진 탐색 트리 이용한 정렬 로직
1) 이진 탐색 트리에서 왼쪽 자식노드는 부모와 오른쪽 자식노드보다 값이 작다.
2) 왼쪽 자식 노드를 중위 순회한다.
3) 왼쪽 자식 노드 모두 순회 했다면 본인 원소 저장 후 오른쪽 자식 노드를 중위 순회한다.

• 시간복잡도

  원소 이진 탐색 트리 삽입 시간 + 중위 순회 시간
  n ⅹ O(log n) + O(n) = O(nlog n)

---

🔎 시간 복잡도 정리

방법	시간복잡도
삽입	O(n^2)
선택	O(n^2)
거품	O(n^2)
퀵	O(n^2) 또는 O(nlog n)
합병	O(nlog n)
힙	O(nlog n)
이진탐색트리	O(nlog n)