[자료구조/Java] 힙(heap)

✔ 목차

1. 힙(heap)이란?
2. 힙 종류
3. 힙 구현
4. 힙 연산
5. 시간복잡도
6. 힙 응용 - 우선순위 큐
7. 힙 응용 - 힙 정렬

---

🔎 힙(heap)이란?

• 완전 이진트리
• 중복값 허용
• 흽의 왼쪽 부트리와 오른쪽 부트리 모두 힙
• 최댓값이나 최솟값 빠르게 찾기 용이
• 느슨한 정렬 상태

---

🔎 힙 종류

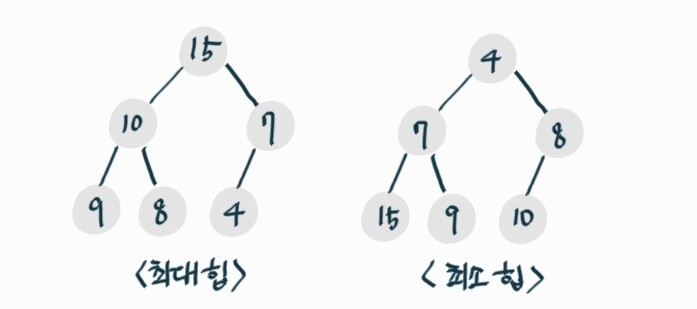
• 최대 힙(max heap)
• 최소 힙(min heap)

• 최대 힙(max heap)
  • 부모 노드 값이 자식 노드의 값보다 크거나 같음
  • 루트 값은 저장된 원소 중 가장 큼

• 최소 힙(min heap)
  • 부모 노드 값이 자식 노드의 값보다 작거나 같음
  • 루트 값은 저장된 원소 중 가장 작음

---

🔎 힙 구현

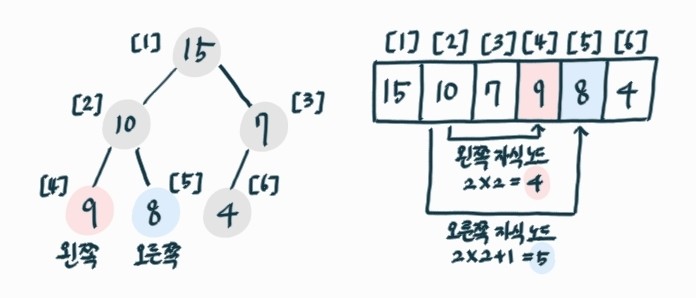
• 배열로 구현
• 인덱스 0 사용하지 않음
• 부모-자식 사이 인덱스 관계
  • 인덱스 i에서 부모인덱스: i/2
  • 인덱스 i에서 왼쪽 인덱스: i * 2
  • 인덱스 i에서 오른쪽 인덱스: ( i * 2 )+1

---

🔎 힙 연산

• 삽인 연산
• 삭제 연산

(모든 예제는 최대 힙으로 한다.)

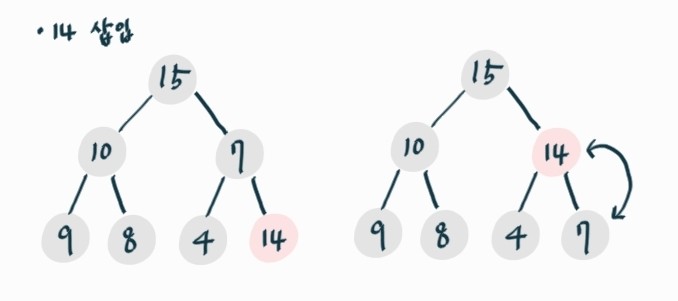
• 삽입 연산
  1) 마지막 위치에 노드 만들어 삽입 -> 구조적 성질 만족
  2-1) 부모 노드보다 값이 작으면 끝
  2-2) 부모 노드보다 값이 크면 부모노드와 스위치
  3) 2번 과정 최대 루트까지 반복 -> 힙의 성질 만족시키기
  

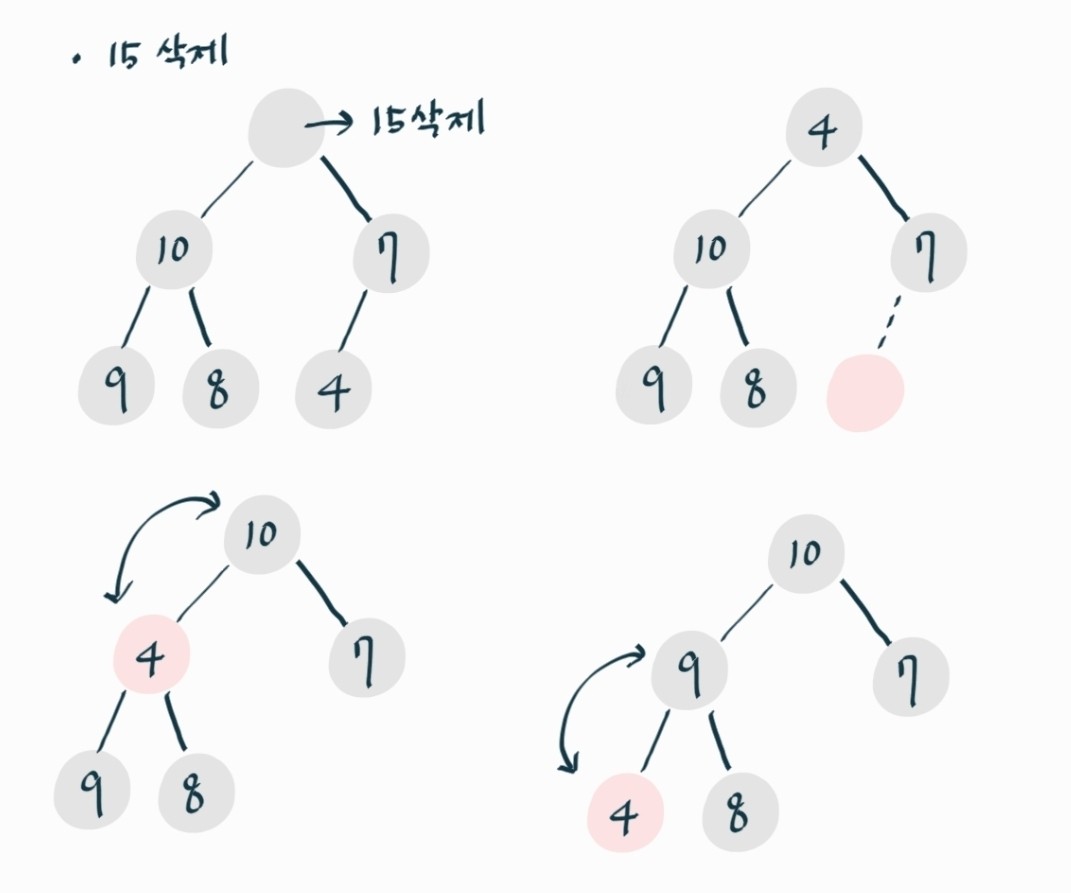
• 삭제연산
  1) 루트 노드 값 제거
  2) 마지막 노드 값 루트로 옮기고 노드 삭제 -> 구조적 성질 만족
  3-1) 자식 노드보다 값 크면 끝
  3-2) 자식 노드보다 값 작으면 스위치
  4) 3번 과정 최대 리프까지 반복 -> 힙의 성질 만족시키기

---

🔎 시간복잡도

• 삽입연산
  • 최악의 경우 교환을 반복하여 리프노드에서 루트노드가 될 수 있음
  • 교환은 O(1)시간에 처리
• 삭제연산
  • 최악의 경우 교환을 반복하여 루트노드에서 리프노드가 될 수 있음
  • 교환은 O(1)시간에 처리

두 연산 모두 최악의 경우 교환 횟수는 힙의 높이(height)가 된다. 힙은 완전 이진 트리이므로 높이가 log_2 n을 넘지 않는다. 따라서 두 연산의 시간복잡도는 O(log n)이다.

연산	시간복잡도
삽입	O(log n)
삭제	O(log n)

---

🔎 힙 응용 1 - 우선순위 큐

• 큐의 선입선출와 달리 우선순위가 높은 데이터가 먼저 나옴
• 힙을 통해 우선순위 큐 구현

자바에서 우선순위 큐 사용하기

---

🔎 힙 응용 2 - 힙 정렬

• 힙 정렬
  1) 정렬할 데이터 n개 하나씩 힙에 삽입 -> O(n) * O(logn)
  2) 최댓값 차례로 하나씩 삭제하여 보관 -> O(n)

• 시간복잡도: O(nlogn) + O(n) = O(nlogn)