Algorithm

생각보다 까다로웠던 골드 4 구현 문제궁수들을 배치하는 모든 경우의 수 mC3에 경우에 대해서 각각의 케이스에 대해 잡을 수 있는 적들의 수를 세면 되는 문제N과 M이 15로 매우 작아서 시간복잡도는 그렇게 생각 안해도 되는 문제for 궁수를 배치하는 경우의 수 wh

간단한 DFS 문제쿼리문이 1일 경우 start에서 end 까지 dfs를 돌리면서 최종 end까지 배달하면서 놓는 우유를 answer\[] 배열을 정의해서 더해준다 . 시간복잡도는 대략 O(NQ) = 1000 1000인 백만으로 충분히 통과한다.이보다 어려운버전인

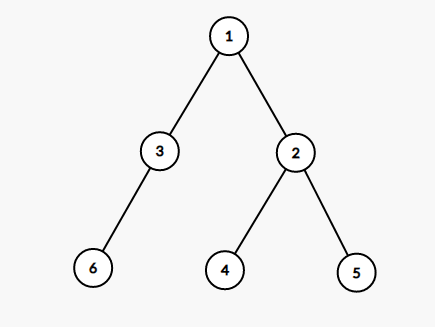
전제 : BFS로 순회 할 때 현재 정점의 깊이를 저장하면 그 배열은 오름차순으로 정렬이 된다. 위 전제를 기반으로 문제를 풀었으며 몇 가지 예외를 처리해주어야 한다. 예외 1. 정

간단한 다이나믹 프로그래밍 문제dp현재 가지고 있는 돈으로 가장 큰 방 번호 로 정의 하였고풀이는loop를 두번 돌면서for 현재 가지고 있는 돈 ~ m for 방번호, 방 번호의 값 ~ Pn-1 dp현재 가지고 있는 돈 + 방 번호의 값 = max(dp현재

조합에 관한 문제학교 다닐때 풀었던 조합 문제를 프로그래밍 해서 푸는문제문제는 2가지 파트로 나뉜다집 -> 토스트 까지의 경우의 수토스트 -> 학교 까지의 경우의 수점화식은 dpy = dpy-1 + dpy 시간 복잡도는 루프를 두번 돌아서 O(N^2)이다!먼저 집 ->

먼저 처음 시작 지점에서 갈 수 있는 버스 노선들을 전부 큐에더가 저장을 한다.버스 시작점과 종착점 사이에 시작 지점이 있으면 큐에다가 저장이제 큐를 돌면서 순회를 하게 되는데지금 내가 탄 버스가 수평일 경우 :다음 버스가 수직일 경우 : 두 선분을 비교해서 교차점이

https://www.acmicpc.net/problem/3176N개의 정점과 N-1개의 도로로 이루어진 도로 네트워크이 문제를 풀 정도면 트리인것과 LCA를 이용해서 풀어야 한다는 것쯤은 쉽게 눈치챌수 있을텐데도로중에서의 최솟값과 최댓값을 어떻게 구할것인지가

P5 치고 상당히 어려웠다알고리즘 자체보다는 메모리랑 시간초과가 상당히 빡빡해서 최적화 작업이 꽤나 빡셌다.데이터 추가되고 급 난이도 상승되어서 재채점 결과보니 상당수가 갈려나간걸 볼 수 있었다.데이터 추가 1/10이 갈려나감 ;; 데이터 추가 되고 난이도 평가가 올