
출처
백준 - 블랙잭
🔎 문제
카지노에서 제일 인기 있는 게임 블랙잭의 규칙은 상당히 쉽다. 카드의 합이 21을 넘지 않는 한도 내에서, 카드의 합을 최대한 크게 만드는 게임이다. 블랙잭은 카지노마다 다양한 규정이 있다.
한국 최고의 블랙잭 고수 김정인은 새로운 블랙잭 규칙을 만들어 상근, 창영이와 게임하려고 한다.
김정인 버전의 블랙잭에서 각 카드에는 양의 정수가 쓰여 있다. 그 다음, 딜러는 N장의 카드를 모두 숫자가 보이도록 바닥에 놓는다. 그런 후에 딜러는 숫자 M을 크게 외친다.
이제 플레이어는 제한된 시간 안에 N장의 카드 중에서 3장의 카드를 골라야 한다. 블랙잭 변형 게임이기 때문에, 플레이어가 고른 카드의 합은 M을 넘지 않으면서 M과 최대한 가깝게 만들어야 한다.
N장의 카드에 써져 있는 숫자가 주어졌을 때, M을 넘지 않으면서 M에 최대한 가까운 카드 3장의 합을 구해 출력하시오.
🚫 입력 및 출력
<입력>
첫째 줄에 카드의 개수 N(3 ≤ N ≤ 100)과 M(10 ≤ M ≤ 300,000)이 주어진다.
둘째 줄에는 카드에 쓰여 있는 수가 주어지며, 이 값은 100,000을 넘지 않는 양의 정수이다.
합이 M을 넘지 않는 카드 3장을 찾을 수 있는 경우만 입력으로 주어진다.
<출력>
첫째 줄에 M을 넘지 않으면서 M에 최대한 가까운 카드 3장의 합을 출력한다.
💻 입출력 예
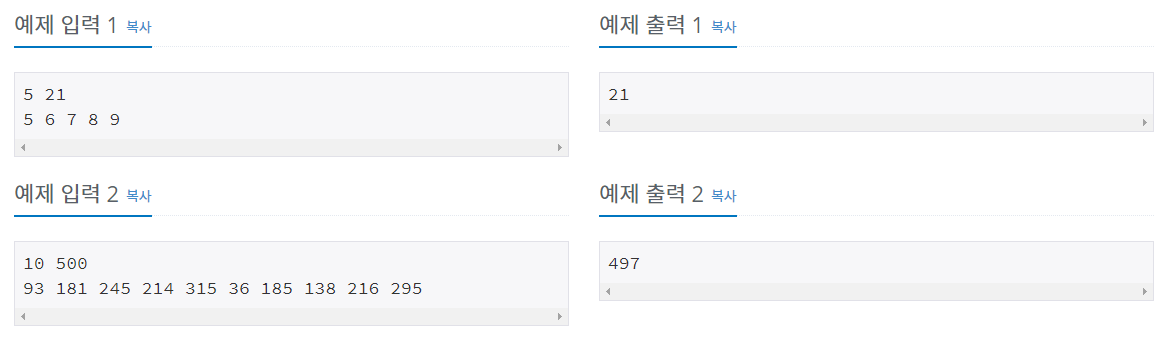
📄🤔 코드 및 풀이과정
🔹 1번
import java.util.ArrayList;
import java.util.Collections;
import java.util.HashSet;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[] cards = new int[n];
for (int i = 0; i < n; i++) {
cards[i] = scanner.nextInt();
}
int answer = play(cards, m);
System.out.println(answer);
}
private static int play(int[] cards, int m) {
HashSet<Integer> hs = new HashSet<>();
for (int i = 0; i < cards.length-2; i++) {
for (int j = i+1; j < cards.length-1; j++) {
for (int k = j+1; k < cards.length; k++) {
hs.add(cards[i]+cards[j]+cards[k]);
}
}
}
ArrayList<Integer> list = new ArrayList<>(hs);
Collections.sort(list);
int first = 0;
int second = list.size()-1;
int halfValue = 0;
int halfIndex = 0;
while(second - first > 4) {
halfIndex = (first + second) / 2;
halfValue = list.get(halfIndex);
if(halfValue < m) {
first = halfIndex;
}else if(halfValue > m) {
second = halfIndex;
}else {
return halfValue;
}
}
int answer = 0;
for (int i = first; i <= second; i++) {
if(list.get(i) > m) {
answer = list.get(i-1);
break;
}else if(i == second){
answer = list.get(i);
}
}
return answer;
}
}🔸 1번 풀이
처음 코드는
더한 값들의 경우의 수를 중복 없이 저장하기 위해 HashSet에 저장하고
이를 ArrayList에 옮겨 정렬한 뒤 이진 검색을 활용하였다.
특정한 값을 입력받아 찾는 것이 아니라
특정한 값보다 작은 값 중 가장 큰 값을 찾는 문제였기 때문에
이진 검색으로 찾을 범위를 확연하게 줄인 뒤
범위 내에서 원하는 값을 찾는 로직을 구현했다.
결과는 성공적으로 통과했다.
메모리 : 22912 KB / 처리시간 : 268 ms
하지만 문제를 통과하고 나서
해당 문제가 이진 검색 알고리즘이 아닌
브루트포스(완전탐색) 알고리즘을 활용해야 한다는 것을 알고
새로이 문제를 풀어봤다.
🔹 2번
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[] cards = new int[n];
for (int i = 0; i < n; i++) {
cards[i] = scanner.nextInt();
}
int answer = play(cards, m, n);
System.out.println(answer);
}
private static int play(int[] cards, int m, int n) {
int answer = 0;
int sum = 0;
for (int i = 0; i < n-2; i++) {
for (int j = i+1; j < n-1; j++) {
for (int k = j+1; k < n; k++) {
sum = cards[i]+cards[j]+cards[k];
if(sum <= m && sum > answer) answer = sum;
}
}
}
return answer;
}
}🔸 2번 풀이
1번에서 이진 검색을 통해
모든 수를 탐색하지 않고 일부만 탐색하려던 것과 달리
이번에는 3중 for문에서 값을 저장하지 않고,
입력받은 값보다 작은 수면서 기존 answer보다 큰 값을 answer 변수에 저장하면서
모든 경우의 수를 탐색하는 완전 탐색(브루트포스)을 하였다.
1번 방법에서 이진 검색을 위해 값을 저장하고, 정렬한 뒤 탐색을 하는 탓에 오히려 완전 탐색을 하는 2번 방법이 더 빠른 처리속도로 통과하였다.
메모리 : 12964 KB / 처리시간 140 ms
😳❕ 소감 & 느낀점
처음엔 경우의 수가 무수히 많을 경우 완전 탐색을 하면
너무 느려지지 않을까 하여 이진 검색을 활용해서 문제를 풀어봤다.
하지만 이진 검색을 하기 위해 해야 하는 저장, 정렬 과정이 처리 지연을 불러왔는지
오히려 완전탐색보다 더 느린 결과가 나와버렸다.
코드 또한 완전탐색이 훨씬 깔끔하게 나왔다.
이미 배열이나 컬렉션에 값이 저장되어 있는 상태에서 값을 찾는 것이라면
완전 탐색을 하며 모든 경우의 수를 찾는 것보다 이진 검색이 빠르겠지만,
이번엔 부수적인 과정을 너무 많이 거친 것 같다.
문제에 따라 적합한 알고리즘이 있으니, 문제를 풀기 전 어떤 알고리즘이 적합할 지 좀 더 생각한 뒤에 문제를 푸는 습관을 들여봐야겠다.
