그리디(Greedy) 알고리즘

탐욕(그리디) 알고리즘

• 최적화 문제를 해결하는 알고리즘이다.

  • 최적화 문제
    가능한 해들 중에서 가장 좋거나 나쁜 해를 찾는 문제이다.

• 입력 데이터 간의 관계를 고려하지 않고 수행 과정에서 '욕심내어' 최소값 또는 최대값을 가진 데이터를 선택한다.

• 근시안적인 선택으로 부분적인 최적 해를 찾고, 이들을 축적하여 문제의 최적 해를 도출한다.

• 특정한 문제를 만났을 때 단순히 현재 상황에서 가장 좋아 보이는 것만을 선택해도 문제를 풀 수 있는지를 파악할 수 있어야 한다.

• 문제에서 '가장 큰 순서대로', '가장 작은 순서대로'와 같은 기준이 존재할 때 적용하면 좋다.

• 거스름돈 문제가 가장 대표적인 그리디 알고리즘 문제이다.

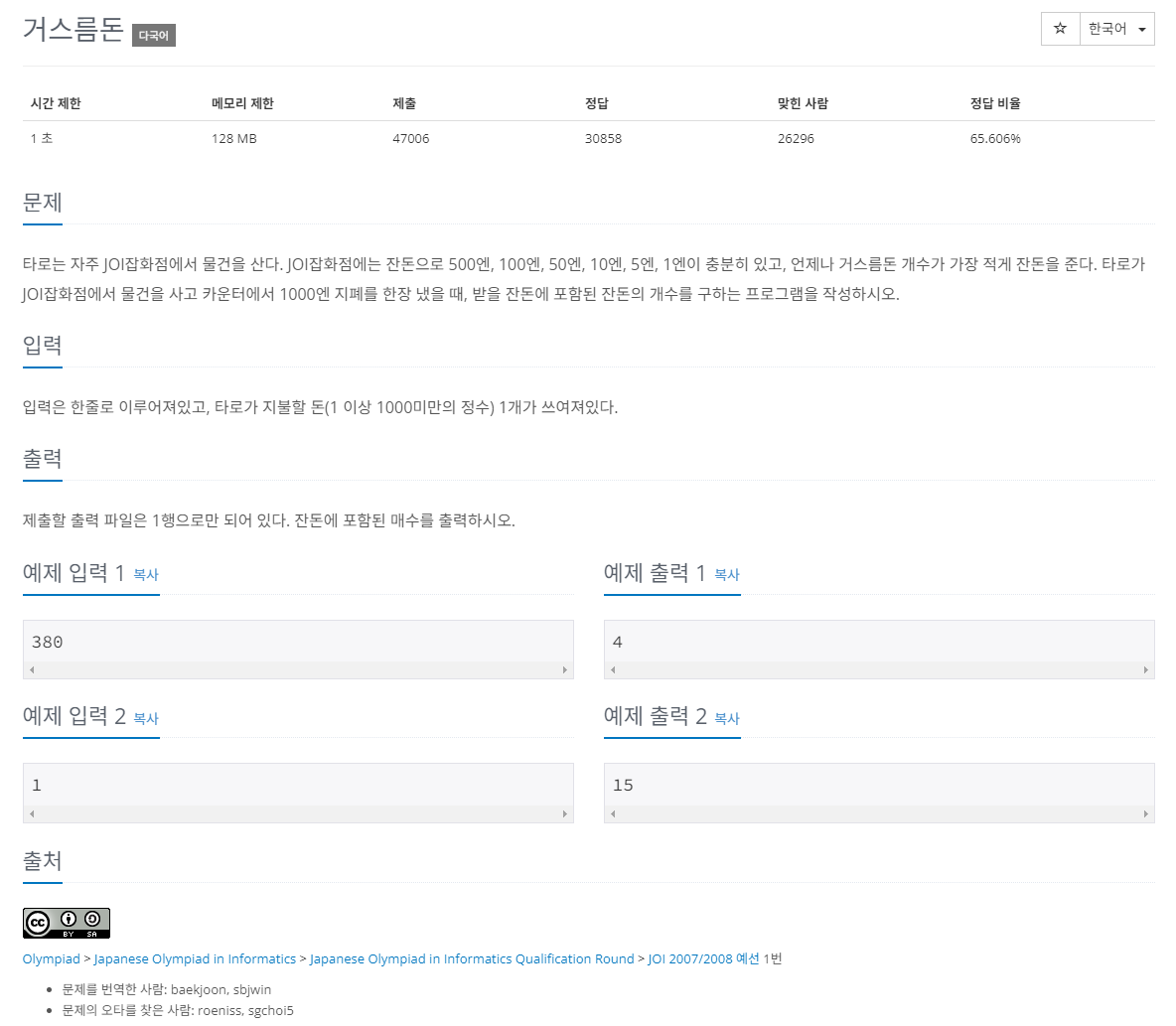
거스름돈 문제

출처: https://www.acmicpc.net/problem/5585

코드

n = int(input())
x = 1000 - n
y = 0
count = 0

coin_types = [500, 100 ,50, 10, 5, 1]

for coin in coin_types:
    y = x // coin
    count += y
    x -= coin * y

print(count)    

그리디 알고리즘의 정당성

• 거스름돈 문제를 그리디 알고리즘으로 해결할 수 있는 이유는 가지고 있는 동전 중에서 큰 단위가 항상 작은 단위의 배수이므로 작은 단위의 동전들을 종합해 다른 해가 나올 수 없기 때문이다.

  • cf. 화폐의 단위가 서로 배수의 형태가 아닌 무작위로 주어진 경우에는 그리디 알고리즘으로 해결할 수 없다.

• 가장 큰 단위의 화폐부터 작은 단위의 화폐까지 차례대로 확인하여 거슬러 주는 작업만 수행하면 된다.

• 문제 유형을 바로 파악하기 힘들다면 그리디 알고리즘을 의심해본다.

• 그리디 알고리즘으로도 풀리지 않는다면 다이나믹 프로그래밍이나 그래프 알고리즘 등으로 문제를 해결할 수 있는지 고민해본다.

해당 글은 다음 도서의 내용을 정리하고 참고한 글임을 밝힙니다. 보다 자세한 내용은 아래 책에서 확인할 수 있습니다.
나동빈, ⌜이것이 취업을 위한 코딩 테스트다 with 파이썬⌟, 한빛미디어, 2020, 604쪽