DFS와 BFS의 기본적인 개념을 알고 이를 함수로 구현만 할 수 있으면 쉽다
BFS - 너비 우선 탐색
: 한 단계씩 내려가면서, 해당 노드와 같은 단계에 있는 노드(형제 노드)를 먼저 탐색하는 방식
DFS - 깊이 우선 탐색
: 한 노드의 자식을 타고 끝까지 탐색한 후, 다시 돌아와 다른 형제노드의 자식노드를 타고 내려가며 탐색하는 방식
- BFS, DFS 그림으로 표현하기
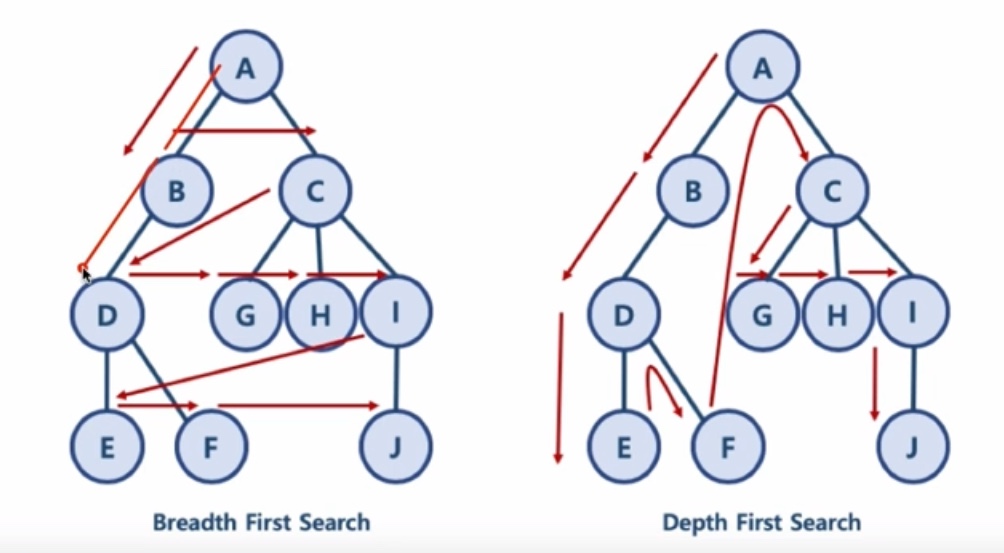
위 탐색 방법을 그림으로 표현하면 다음과 같다.
왼쪽이 BFS, 오른쪽이 DFS
- BFS, DFS 탐색 배열로 알아보기
[[2,3,4],
[1,4],
[1,4],
[1,2,3]]
이러한 배열이 있을 때
1부터 탐색한다고 하면
- BFS : 1-> 2-> 3 -> 4
- DFS : 1-> 2-> 4 -> 3
[[2,3],
[1,5],
[1,4],
[3,5],
[2,4]]
위 배열을 1부터 탐색한다면
- BFS : 1 -> 2 -> 3 -> 5 -> 4
- DFS : 1 -> 2 -> 5 -> 4 -> 3
- DFS, BFS 함수로 표현하기
func dfs()
bfs는 방문한 정점의 자식 노드들을 계속 타고 들어가야하므로
재귀함수로 구현되어야한다.
방문했던 정점을 또다시 방문하지 않기 위해서
check 배열을 사용하여 방문여부를 저장하였다.
func dfs(_ now:Int) {
check[now] = true
result += "\(now) "
for i in graph[now] {
if !check[i] {
dfs(i)
}
}
}
func bfs()
dfs는 정점의 형제 노드들을 먼저 탐색해야하는데,
이때 형제 노드들의 순서와, 종류를 잊지 않기 위해서 큐를 사용하여야한다.
방문해야하는 노드(need_visited)와
방문한 노드(visited)를 나타낼 두 개의 큐가 필요하다.
방문해야하는 노드에는 해당 노드의 형제 노드들을 저장하고,
방문한 노드에는 방문한 노드를 저장한다.
func bfs(_ now: Int) {
var needVisited: [Int] = [now]
var visited = [Int]()
while !needVisited.isEmpty {
let node = needVisited.removeFirst()
if !visited.contains(node) {
visited.append(node)
result += "\(node) "
needVisited.append(contentsOf: graph[node].sorted())
}
}
}
- 방문한 노드는 순서가 상관없기 때문에 배열이 아닌 집합으로 나타내어도 된다
최종 코드
import Foundation
let line = readLine()!.split(separator: " ").map{Int(String($0))!}
let N = line[0]
let M = line[1]
let V = line[2]
var graph : [[Int]] = Array(repeating: [], count: N+1)
var check = Array(repeating: false, count: N+1)
var result = ""
for _ in 0..<M {
let relation = readLine()!.split(separator: " ").map{Int(String($0))!}
let a = relation[0]
let b = relation[1]
graph[a].append(b)
graph[b].append(a)
graph[a].sort()
graph[b].sort()
}
func dfs(_ now:Int) {
check[now] = true
result += "\(now) "
for i in graph[now] {
if !check[i] {
dfs(i)
}
}
}
func bfs(_ now: Int) {
var needVisited: [Int] = [now]
var visited = Set<Int>()
while !needVisited.isEmpty {
let node = needVisited.removeFirst()
if !visited.contains(node) {
visited.insert(node)
result += "\(node) "
needVisited.append(contentsOf: graph[node])
}
}
}
dfs(V)
print(result)
result = ""
bfs(V)
print(result)