하노이탑 이동을 이제 완전히 이해할 수 있게 되었다. 야호 -!
수많은 글보다 하나의 유투브 영상이 도움이 되었는데
바로 이것!
차이나는 클라스에서 어떤 교수님..(?) 께서 설명해주신 영상인데 정말 큰 도움이 되었다. 이거만 보면 누구라도 하노이탑 알고리즘 이해 완 !!
위 영상을 토대로 다시 정리해보자면
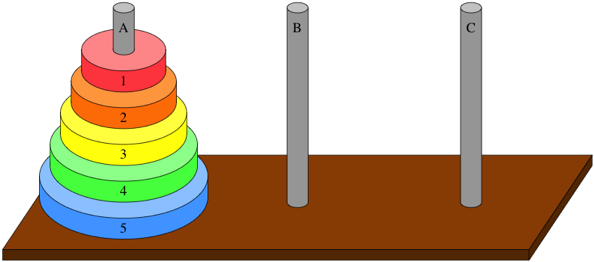
하노이탑 알고리즘이란?
N개의 원판을 규칙을 만족하며 원하는 위치로 이동시키는 알고리즘이다.

이 때, 지켜야하는 규칙이란 다음과 같다
- 한 번에 하나의 원판만 이동 가능
- 원판은 위의 것이 아래의 것보다 작아야한다
재귀로 표현하는 하노이탑 알고리즘
하노이탑 알고리즘 구현을 차례로 알아보면 다음과 같다
1) n-1개의 원판을 두 번째 기둥으로 이동

- 가장 아래에 있는 N원판을 세 번째 기둥으로 이동시키기 위해서 가장 먼저 n-1개의 원판을 보조 기둥으로 이동시켜야 한다.
2) n번째 원판을 세 번째 기둥으로 이동

3) n-1개의 원판을 세 번째 기둥으로 이동

따라서 이 하노이즘 알고리즘을 재귀로 표현해보면
f(n)을 N개의 원판을 이동하는데 필요한 횟수라고 할때
f(n) = 1 + 2 * f(n-1) 이다.
이제 하노이탑 알고리즘은 이해가 되었으니 문제를 풀어보자
백준 11729 - 하노이탑 이동 순서
이 문제에서는 원판을 이동시키기 위해 필요한 최소 횟수와 더불어 각 원판의 이동 위치 또한 출력해야한다.
이 블로그 포스팅을 참고하여 풀이하였다.
- 재귀함수 구현하기
1) 재귀함수 뼈대 구현하기
먼저 위에서 재귀로 구현된 f(n)을 작성하면 다음과 같다
/// N개의 원판을 세 번째 기둥으로 이동
func hanoi(N) {
/// N - 1 개의 원판을 두 번째 기둥으로 이동
func hanoi(N - 1)
/// N 번째 원판을 세 번째 기둥으로 이동
/// N - 1 개의 원판을 세 번째 기둥으로 이동
func hanoi(N - 1)
}따라서 매개변수로는
- 옮길 원판의 갯수
- 출발 기둥
- 도착 기둥
- 보조 기둥
이 필요하다
2) 재귀함수 매개변수 추가하기
매개변수를 추가해서 구현해보면 아래와 같다.
/// N개의 원판을 세 번째 기둥으로 이동
func hanoi(num: Int, from: Int, to: Int, assist: Int) {
/// N - 1 개의 원판을 두 번째 기둥으로 이동
func hanoi(num : num - 1, from: from, to: assist, assist: to)
/// N 번째 원판을 세 번째 기둥으로 이동
/// N - 1 개의 원판을 세 번째 기둥으로 이동
func hanoi(num: num - 1, from: assist, to: to, assist: from)
}3) 재귀함수 종료조건 추가하기
이 매개변수의 종료조건은 추가해주면 다음과 같다.
/// N개의 원판을 세 번째 기둥으로 이동
func hanoi(num: Int, from: Int, to: Int, assist: Int) {
/// hanoi 재귀함수 종료 조건
if num == 1 {
return
}
/// N - 1 개의 원판을 두 번째 기둥으로 이동
func hanoi(num : num - 1, from: from, to: assist, assist: to)
/// N 번째 원판을 세 번째 기둥으로 이동
/// N - 1 개의 원판을 세 번째 기둥으로 이동
func hanoi(num: num - 1, from: assist, to: to, assist: from)
}- 옮겨야하는 원판의 갯수가 하나 남았을 때 종료된다.
4) 원판 이동 위치, 횟수 추가하기
var answer = ""
var count = 0
/// N개의 원판을 세 번째 기둥으로 이동
func hanoi(num: Int, from: Int, to: Int, assist: Int) {
/// hanoi 재귀함수 종료 조건
if num == 1 {
answer += "\(from) \(to)\n"
count += 1
return
}
/// N - 1 개의 원판을 두 번째 기둥(=보조기둥)으로 이동
func hanoi(num : num - 1, from: from, to: assist, assist: to)
/// N 번째 원판을 세 번째 기둥으로 이동
answer += "\(from) \(to)\n"
count += 1
/// N - 1 개의 원판을 세 번째 기둥으로 이동
func hanoi(num: num - 1, from: assist, to: to, assist: from)
}이렇게 하면 끝!
- 전체 풀이 코드
import Foundation
let N = Int(readLine()!)!
var answer = ""
var count = 0
func hanoi(num: Int, from: Int, to: Int, assist: Int) {
if num == 1 {
answer += "\(from) \(to)\n"
count += 1
return
}
hanoi(num: num - 1, from: from, to: assist, assist: to)
answer += "\(from) \(to)\n"
count += 1
hanoi(num: num - 1, from: assist, to: to, assist: from)
}
hanoi(num: N, from: 1, to: 3, assist: 2)
print(count)
print(answer)많은 블로그 글들을 읽었지만.. 이해하기가 쉽지 않았는데 위 영상으로 하노이탑 알고리즘을 이해할 수 있게 되어 너무너무 행복하다!
다른 분들도 꼭 저 영상을 통해 쉽게 이해하셨으면 해서 포스팅으로 남긴다 🥹👍🏻🫶🏻