Jack goes to Rapture

사이트: HackerRank
난이도: 미디움
분류: Graph Theory

문제

무방향 가중치 그래프가 주어지고 노드 n개가 주어질 때, 1번 노드에서 n번 노드까지의 거리중 가장 적은 비용이 드는 값을 찾아서 반환하라.

각 노드간 가중치가 존재하며 다음 노드로 이동시 가중치 값을 다음과 같이 계산한다.
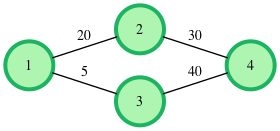
1->2->4로 이동한다고 했을 때, 1->2의 가중치는 20, 2->3으로 이동하면 30이다. 이후 값에서 이전 값을 뺀 나머지가 다음 비용으로 계산되며, 따라서 값은 20 + (30 - 20) = 30이 되게 된다.

1. 나의 풀이

다익스트라 알고리즘으로 접근하는 것이 맞을지 고민하다가, 가중치 계산이 우선순위 큐와 맞지 않을 것 같아서 dfs로 해결하려고 했다. 그러나 생각만큼 잘 되지 않았고, 풀이를 찾아보게 되었다.

function getCost(gNodes, gFrom, gTo, gWeight) {
    // Print your answer within the function and return nothing
    const graph = Array.from(
        new Array(gNodes + 1),
        () => []
    );
    
    for (let i = 0; i < gFrom.length; i++) {
        graph[gFrom[i]].push([gTo[i], gWeight[i]]);
    }
    
    const stack = [[1, 0]];
    const visited = Array.from(new Array(gNodes + 1), () => false);
    visited[1] = true;
    
    let result = Infinity;
    while(stack.length) {
        const [current, cWeight] = stack.pop();
        
        for (const [next, weight] of graph[current]) {
            const nWeight = cWeight + Math.max(weight - cWeight, 0);

            if (next === gNodes) {
                result = Math.min(result, nWeight);
                
            } else if (!visited[next]) {
                stack.push([next, nWeight]);
            }
        }
    }
    
    console.log(result);
}

2. 다른사람의 풀이

function getCost(gNodes, gFrom, gTo, gWeight) {
    // Print your answer within the function and return nothing
    const edges = [];
    for (let i = 0; i < gWeight.length; i++) {
        edges.push([gFrom[i], gTo[i], gWeight[i]]);
        edges.push([gTo[i], gFrom[i], gWeight[i]]);
    }

  	// cost를 계산할 변수를 생성한다.
  	// 0번째 인덱스를 통해 계산된 코스트가 있는지 확인한다.
  	// 1번째부터 시작이므로 1번째 노드의 가중치는 0이다.
    const costs = [ true, 0, ...Array(gNodes - 1).fill(Infinity) ];
    while (costs[0]) {
        costs[0] = false;

        for (const [u, v, w] of edges) {
            if (costs[v] > costs[u] && costs[v] > w) {
              	// 다음 노드로의 가중치가 계산되었다면, 0번째 인덱스를 true로 변경한다.
                costs[0] = !!(costs[v] = Math.max(costs[u], w))
            }
        }
    }
    
  	// 마지막 노드까지의 가중치 값이 계산되었다면 Infinity가 아니므로 그 값을 반환하면 된다.
  	// 반대로 Infinity일 경우 NO PATH EXISTS를 반환한다.
    console.log(
        costs[gNodes] !== Infinity 
            ? costs[gNodes] 
            : 'NO PATH EXISTS'
    );
}