메모리의 주소
메모리 주소는 논리적 주소(가상 주소)와 물리적 주소로 구분된다.
논리적 주소
- 프로세스마다 독립적으로 가지는 주소 공간
- 각 프로세스마다 0번지부터 시작한다.
- cpu가 실제로 보고 있는 주소다.
물리적 주소
- 메모리에 실제 올라가는 위치를 말한다.
어떤 코드를 컴파일하여 프로그램을 만들면 그 때 명령어들과 변수들의 논리적 주소가 결정된다. 이것이 실제로 동작하려면 메모리에 프로세스를 올려야한다. 이 때 논리적 주소가 실제 물리적 주소로 변환되어야 한다.
주소 바인딩
논리적 주소를 물리적 주소로 변환하는 과정을 주소 바인딩이라고 하는데, 물리적 주소가 언제 결정되느냐에 따라 3가지로 구분된다.
compile time binding
- 컴파일시에 물리적 메모리 주소가 결정된다.
- 만약 물리적 메모리 주소에서의 시작 위치 변경시 재컴파일한다.
load time binding
- 프로그램이 시작될때 결정된 논리적 주소를 loader의 책임하에 물리적 메모리 주소를 부여한다.
- 프로그램이 종료될 때까지 물리적 주소가 고정된다.
execution time binding( = run time binding)
- 수행이 시작된 이후에도 프로세스의 메모리 상 위치를 옮길 수 있다.
- CPU가 주소를 참조할 때마다 해당 데이터가 물리적 메모리의 어느 위치에 있는지 점검한다.
- 하드웨어적인 지원이 필요 -> MMU
MMU
mmu는 논리적 주소를 물리적 주소로 매핑해주는 하드웨어다. mmu에는 base register와 limit register가 존재한다. base register는 물리 메모리상에서 프로그램의 시작 주소를 저장하고 있고, limit register는 프로그램의 최대 크기, 즉 한 프로그램에서 접근할 수 있는 논리적 주소의 최대값을 저장하고 있다.
따라서 mmu는 사용자 프로세스가 cpu에서 수행되며 생성해내는 모든 주소값에 대하여 먼저 limit register의 값을 넘지 않는지 체크한다. 넘지 않는다면 base register(relocation register)의 값을 더한다. 이것이 논리적 주소 -> 물리적 주소의 변환이 된다.
예를 들어, 프로세스의 논리적 주소가 0~3000이고, 메모리에서는 12000부터 시작된다고 하자. 그러면 base register에는 12000이 저장되어있고, limit register에는 3000이 저장되게 된다. 만약 cpu가 논리적 주소 1500에 접근하고 싶다고 하면, 이 값이 limit register의 값 3000을 넘지 않는지 확인해야한다. 넘지 않는다면 base register의 값과 논리적 주소의 값 12000 + 1500을 하여 실제 물리적 주소로 변환한다.
이렇게 하는 이유는, 프로그램의 악의적인 주소 요청을 차단하기 위해서다. 한 프로그램이 다른 프로그램에 영향을 미쳐서는 안되기 때문이다.
이런 모든 작업은 하드웨어에서 일어나는 일이며, 위에서 설명했듯이 cpu는 여전히 프로그램의 논리적 주소를 보고 있다. 또한 사용자 프로그램 역시 논리적 주소만을 다루며 물리적 주소를 볼 수 없고 알 수 없다.
여러가지 용어
dynamic loading
- 프로세스 전체를 메모리에 미리 다 올리는 것이 아니라 해당 루틴이 불려질 때 메모리에 로드하는 방법이다.
- 운영체제의 특별한 지원 없이 프로그램 자체에서 구현 가능하다.(OS는 라이브러리를 통해 지원 가능)
overlays
- 메모리에 프로세스의 부분 중 실제 필요한 정보만을 올린다.
- 프로세스의 크기가 메모리의 크기보다 클 때 유용하다.
- 작은 공간의 메모리를 사용하던 초창기 시스템에서 수작업으로 프로그래머가 구현하던 작업이다.
swapping
- 메모리 부족등을 이유로 프로세스를 일시적으로 메모리에서 디스크로 쫓아내는 것이다.
swap in / swap out
- swapping할 때 프로세스를 메모리에서 디스크로 쫓아내는 것을 swap out, 다시 메모리로 불러들이는 것을 swap in이라고 한다.
- 일반적으로 중기 스케줄러에 의해 swap out 시킬 프로세스를 선정한다.
- 주로 우선순위가 낮은 프로세스를 swap out하고, 높은 프로세스를 메모리에 올려 놓는다.
- swap time은 대부분 transfer time(swap되는 양에 비례하는 시간)이다.
static linking
- 라이브러리가 프로그램의 실행 파일 코드에 포함된다.
- 실행 파일의 크기가 커진다.
- 동일한 라이브러리를 각각의 프로세스가 메모리 올리므로 메모리 낭비 ex) printf 함수의 라이브러리 코드
dynamic linking
- 라이브러리가 프로그램 실행시 link된다.
- 라이브러리 호출 부분에 라이브러리 루틴의 위치를 찾기 위한 stub이라는 작은 코드를 둔다.
- 라이브러리가 이미 메모리에 있으면 그 루틴의 주소로 가고 없으면 디스크에서 읽어온다.
- 운영체제의 도움이 필요하다.
메모리 할당
메모리는 일반적으로 두 영역으로 나뉜다.
1. OS 상주 영역(커널)
-> 인터럽트 벡터와 함께 낮은 주소 영역을 사용한다.
2. 사용자 프로세스 영역
-> 높은 주소 영역을 사용한다.
여기서 다루는 것은 사용자 프로세스 영역에 대한 할당 방법이다. 두 가지로 나뉜다.
연속 할당
- 각각의 프로세스가 메모리의 연속적인 공간에 적재되도록 하는 것
- fixed partition allocation, variable partition allocation
불연속 할당
- 프로그램을 구성하는 주소 공간을 쪼개서 메모리의 여러 영역에 분산되어 올라감
- 현대의 운영체제가 사용하는 기법이다.
- paging, segmentation, paged segmentation
연속 할당
연속 할당에는 두 가지 방법이 존재한다.
고정 분할 방식(fixed partition allocation)
- 물리적 메모리를 미리 똑같은 크기, 개수로 분할해놓는 방식
- 물리적 메모리를 미리 분할해서 그 곳에 프로그램을 올린다.
- 이 때 물리적 메모리 공간의 크기가 프로그램보다 작으면 외부 단편화가 발생할 수 있고, 메모리 공간의 크기가 프로그램보다 크면 내부 단편화가 발생할 수 있다.
가변 분할 방식(variable partition allocation)
- 프로그램의 크기를 고려하여 메모리에 할당
- 분할의 크기, 개수가 동적으로 변할 수 있다.
- 프로그램이 종료되고 새로운 프로그램이 실행됐는데, 종료된 프로그램이 반환한 메모리 크기가 새로운 프로그램의 크기보다 작으면 그곳에서 새로운 프로그램을 실행하지 못함 -> 외부 단편화가 발생할 수 있다. 내부 단편화는 발생하지 않는다.
이렇게 프로세스가 메모리에서 할당, 해제를 거치며 메모리 내에 다양한 크기의 빈 공간이 생기게 되는데, 이것을 hole이라고 한다. 가용 메모리 공간이라고 하기도 한다.
프로세스가 도착하면 그 프로세스를 수용가능한 hole을 할당해야한다. 따라서 운영체제는 할당공간과 가용공간에 대한 정보를 유지한다.
가변 분할 방식에서는 size가 n인 요청을 만족하는 적절한 hole을 찾아야 하는 문제가 있다. 이에 대한 해결법은 3가지로 나뉜다.
First-fit
- size가 n 이상인 것중 최초로 찾은 hole에 할당
best-fit
- size가 n 이상인 것중 가장 작은 hole을 찾아서 할당
- hole들의 리스트가 크기순으로 정렬되지 않은 경우 모든 hole의 리스트를 탐색해야함
- 많은 수의 아주 작은 hole들이 생성됨
worst-fit
- 가장 큰 hole에 할당
- 역시 모든 리스트를 탐색해야함
- 상대적으로 아주 큰 hole들이 생성됨
보통 first-fit과 best-fit이 worst-fit보다 속도와 공간이용률 측면에서 효과적인 것으로 알려져있다.
위에서 설명한 외부 단편화 문제를 해결하기 위해 수행할 수 있는 한 가지 방법이 존재한다. 바로 압축(compaction)이라는 기법이다. 이 방법은 사용중인 메모리 영역을 한 곳에 몰고 hole들을 다른 한 곳으로 몰아서 큰 공간을 만들어내는 것이다. 비용이 많이 들며 프로세스의 주소가 실행시간에 동적으로 재배치 가능한 경우에만 수행할 수 있다.
불연속 할당
불연속 할당은 프로세스를 구성하는 주소 공간을 쪼개서 메모리의 여러 영역에 분산하여 올리는 기법이다.
paging
페이징에서는 물리적 메모리를 동일한 크기의 프레임으로 나누고, 논리적 메모리를 동일한 크기의 페이지(프레임과 크기가 같음)로 나눈다. 그리고 각 페이지에 해당하는 프레임을 매핑시켜주는 페이지 테이블이라는 공간을 메인 메모리에 따로 둔 다음, 이것을 이용하여 논리적 주소를 물리적 주소로 변환한다.
외부 단편화는 발생하지 않지만, 내부 단편화는 발생 가능하다.
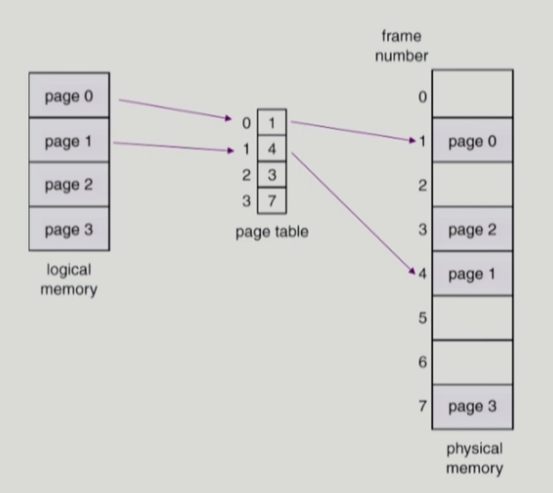
그림처럼 논리적 메모리를 페이지 단위로 나누고, 각 페이지는 물리적 메모리의 프레임이라는 공간에 올라가게 된다. 이 때 어떤 페이지가 어떤 프레임을 참조하는지 나타내는 페이지 테이블을 이용하여 논리적 주소를 물리적 주소로 변환하게 된다. 페이지 테이블에 존재하는 각 행을 엔트리라고 부른다.
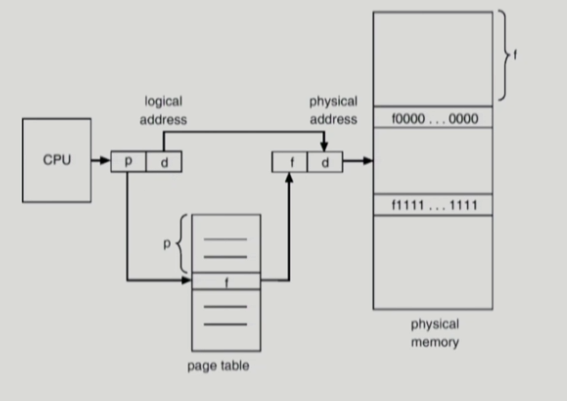
이 그림은 실제로 cpu가 논리적 주소를 물리적 주소로 변환하는 과정을 나타낸 것이다. 그림에서 논리적 주소는 페이지 번호 p와 오프셋 d로 나뉘게 된다. 페이지 테이블에서 p번에 해당하는 엔트리를 찾은 다음, 그곳에 적혀 있는 프레임 번호 f에다가 오프셋 d를 더하여 실제 물리적 주소로 변환하게 된다.
다만, 이렇게 된다면 논리적 주소를 물리적 주소로 변환하기 위해 2번의 과정을 무조건 거쳐야하는데 이러면 시간이 많이 들게 된다. 따라서 페이지 테이블에서 빈번히 접근되는 엔트리를 캐싱하는 TLB를 사용하게 된다.
TLB는 translation look-aside buffer라고 불리는 고속의 하드웨어로, 병렬 검색이 가능하게 한다. 만약 문맥교환이 일어나게 되면 새 프로세스의 페이지 테이블을 캐싱하기 위해 flush를 하게 된다.
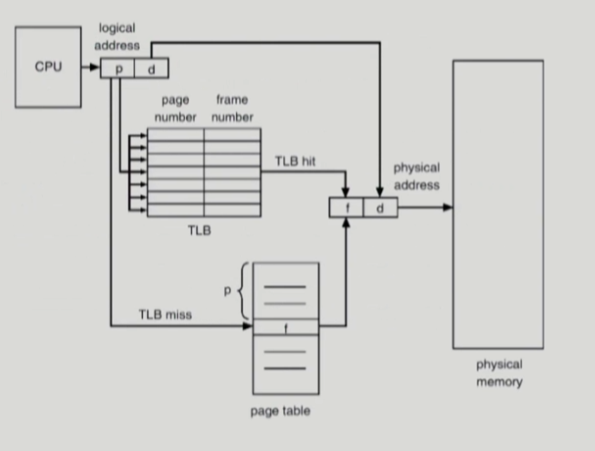
위 그림과 같이 TLB hit면 바로 해당 물리적 주소로 변환하게 되고 TLB miss라면 페이지 테이블에 접근하여 물리적 주소로 변환하게 된다.
two-level page table
현대의 컴퓨터는 주소 공간이 매우 큰 프로그램을 지원한다. 만약 32비트 주소 체계를 사용할시 4gb의 주소 공간이 만들어질 수 있다. 그러나 대부분의 프로그램은 4gb의 주소 공간중 지극히 일부만 사용하므로 페이지 테이블의 공간이 심하게 낭비된다.
이를 해결하기 위해 2단계 페이지 테이블을 사용할 수 있다.
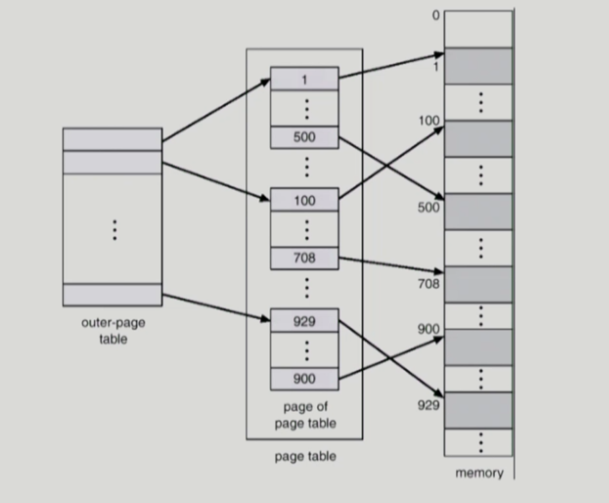
2단계 페이지 테이블은 outer 페이지 테이블과 inner 페이지 테이블로 구분된다. inner 페이지 테이블은 여러 개가 존재하고 프레임 번호를 가지고 있으며 outer 페이지 테이블은 inner 페이지 테이블의 주소를 가지고 있다.
논리적 주소는 다음과 같이 구성된다.

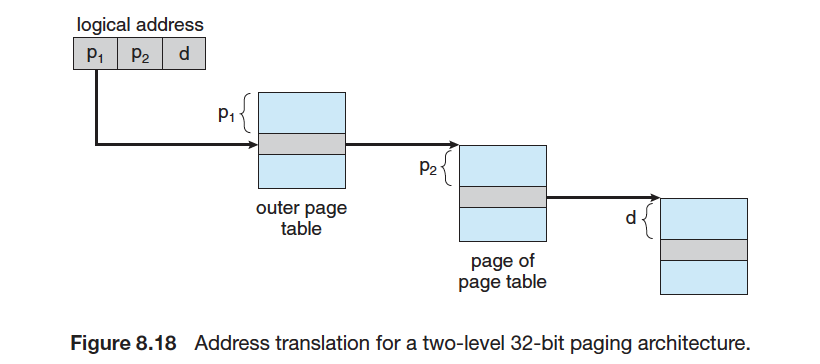
위 그림이 2단계 페이지 테이블의 구조를 잘 나타내준다. p1은 outer 페이지 테이블에서의 변위를 나타내고, 그곳에는 inner 페이지 테이블의 주소가 존재하며 그 주소와 p2 변위를 더하여 엔트리를 찾는다. 그리고 그것을 오프셋 d와 더하여 최종 물리적 주소가 된다.
그렇다면 어떻게 공간의 낭비를 줄일까? 2단계 페이지 테이블에서는 사용되지 않는 주소 공간에 대한 outer 페이지 테이블의 엔트리 값을 null로 처리한다. 이것이 2단계 페이지 테이블을 이용해서 공간을 줄이는 방법이다.
multilevel paging and performance
주소 공간이 더 커지면 다단계 페이지 테이블이 필요할 수 있다. 그런데 이 때 단계가 늘어날 수록 접근시간이 늘어나는데, 이를 TLB를 통해서 줄일 수 있다.
또한 사용하지 않는 페이지가 있어도 그 페이지에 대한 엔트리가 존재해야 한다. 배열 구조이기 때문이다. 따라서 페이지 엔트리에서 페이지 사용여부를 flag로 구분한다.
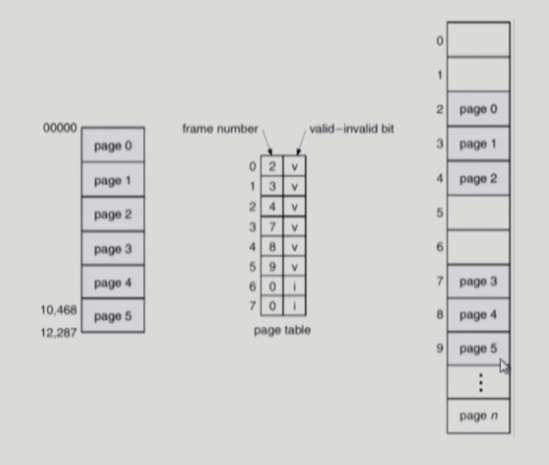
그림처럼 valid flag는 해당 주소의 프레임에 그 프로세스를 구성하는 유효한 내용이 있음을 뜻하고, invalid flag는 그 반대를 뜻한다. 즉, 프로세스가 그 주소 부분을 사용하지 않는 경우, 해당 페이지가 메모리에 올라와있지 않고 swap area에 있는 경우를 뜻한다.
inverted page table
모든 프로세스는 각각 가지고 있는 논리적 주소에 대응하는 페이지 테이블 엔트리가 존재한다. 따라서 페이지 테이블이 많이 있고 크기가 크다.
이에 시스템에 모든 프로세스가 공유하는 페이지 테이블을 하나만 두고, 그대로 그것을 메인 메모리에 사상시키는 방법인 역 페이지 테이블이 존재한다.
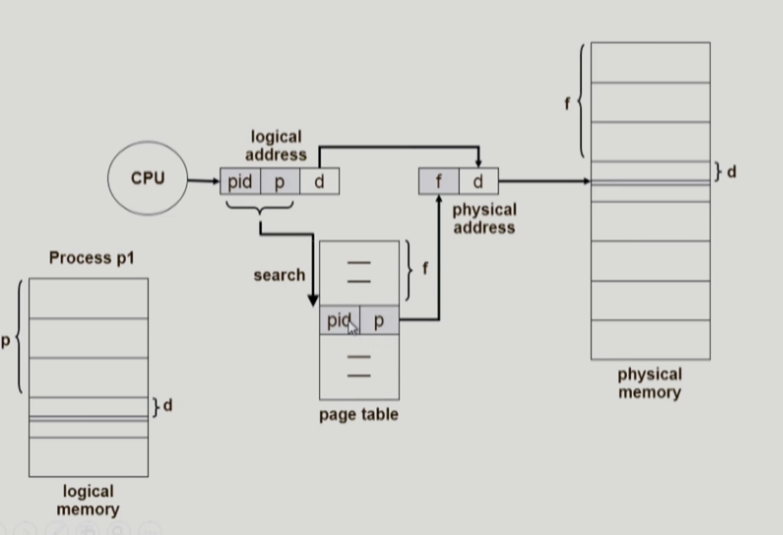
논리적 주소는 pid, 주소 p, 오프셋 d를 가진다. 페이지 테이블은 그대로 메인 메모리에 사상되므로 페이지 테이블의 각 엔트리는 메인 메모리의 각 프레임에 대응한다. 따라서 페이지 프레임 갯수만큼 엔트리가 존재한다.
pid와 p로 페이지 테이블에서 인덱스로 엔트리를 찾는다. 근데 페이지 테이블의 엔트리 인덱스 f는 물리 메모리에서의 프레임 인덱스하고 같으므로 인덱스 f + 오프셋 d를 하여 물리적 주소를 찾아낸다.
역 테이블 페이지의 단점은 최악의 경우 테이블 전체를 탐색해야 한다는 것이다. 이에 대한 조치로 associative register를 사용하는 방법이 있다.
shared page
여러 프로세스에서 공유하는 코드가 있을 수 있다. 그 코드는 read-only로 설정하여 하나만 메모리에 올린다. 그리고 여러 프로세스들이 그것을 공유한다. 이 때 이런 공유 코드는 모든 프로세스의 논리적 주소 공간에서 동일한 위치에 존재해야 한다. 그렇지 않으면 공유가 되지 않기 때문이다.
segmentation
세그먼테이션은 프로그램을 의미 단위의 여러 개의 세그먼트로 구성하는 기법이다. 크게는 프로그램 전체를 하나의 세그먼트로 정의 가능하고 일반적으로는 code, data, stack 부분이 하나씩 세그먼트로 정의된다. 페이지와는 다르게 세그먼트는 정해진 크기가 아니라 프로그램의 크기에 맞게 설정한다.
세그먼테이션은 세그먼트 테이블의 위치를 담고 있는 segment-table base register와 프로그램들이 사용하고 있는 총 세그먼트의 수를 담고 있는 segment-table length register를 이용한다.
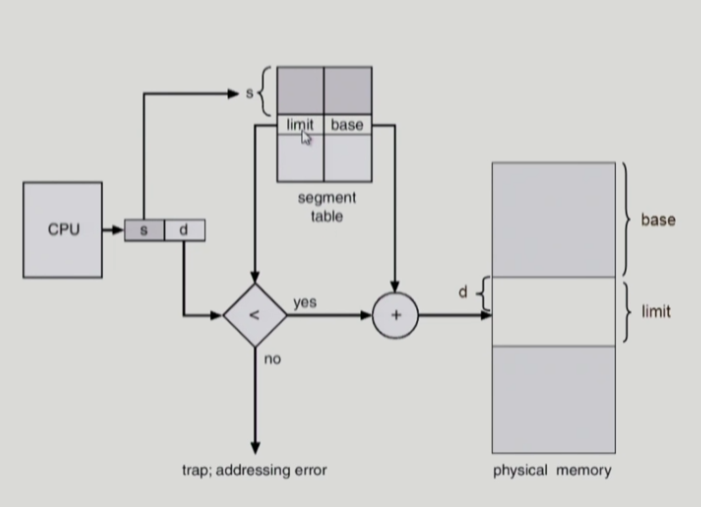
논리적 주소는 세그먼트 번호 s, 오프셋 d로 구성된다. 세그먼트 테이블에서 세그먼트 번호 s를 통해 세그먼트의 물리적 시작 주소인 base와 세그먼트의 길이인 limit이 담긴 엔트리를 찾는다. 그 후에 오프셋과 base를 더해서 물리적 주소로 변경한다.
이 때 두 가지 검사를 하는데 첫 번째는 세그먼트 번호 s가 segment-table length register에 담긴 수보다 크다면 잘못된 정보이므로 trap을 발생시킨다. 두 번째로는 세그먼트의 길이 limit보다 오프셋 d가 크다면 마찬가지로 trap을 발생시킨다.
각 세그먼트에는 유효한 내용인지를 알려주는 valid bit, 권한에 대한 read/wirte/execution bit가 존재한다.
세그먼트는 의미 단위이기 때문에 공유와 보안에 있어 페이징보다 훨씬 효과적이다.
세그먼트의 크기는 동일하지 않으므로 가변분할 방식처럼 외부 단편화가 발생할 수 있다. 또 first fit, best fit이 제일 효율이 좋다. 일반적으로 세그먼테이션이 페이징보다 메모리 낭비가 더 적다.
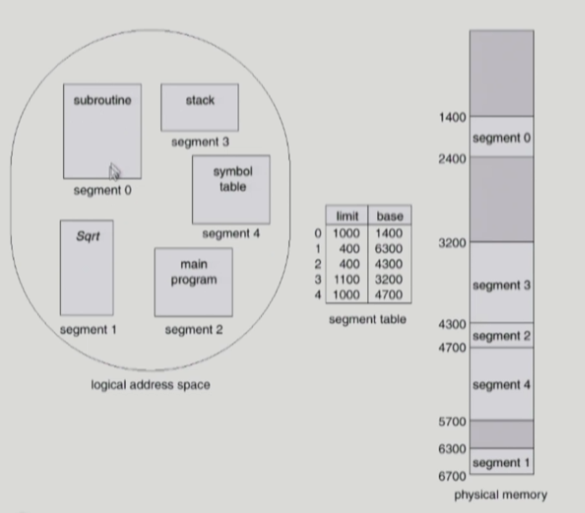
위 그림은 프로그램을 구성하는 세그먼트가 5개일 때 예시다.
paged segmentation
페이징 방식과 세그먼테이션 두 방식을 합친 것이다. 이 방식은 세그먼테이션을 먼저 수행하고 각 세그먼트 별로 페이징을 수행한다. 즉 세그먼트 하나가 여러 개의 페이지로 구성된다. 결국 메모리에 올라갈 때는 페이지 단위로 올라가기 때문에, 세그먼테이션의 단점이 발생하지 않는다.
먼저 논리적 주소는 세그먼트의 번호 s와 오프셋 d로 구성된다. s를 통해 먼저 세그먼트 테이블에서 엔트리를 찾는다. 그 엔트리에는 세그먼트의 길이와 페이지 테이블의 시작 주소(base)가 존재한다. 이 시작주소를 통해 페이지 테이블로 이동할 수 있다. 이 때 세그먼트 길이는 페이지 테이블의 엔트리 갯수가 되며, 오프셋 d가 이 길이를 넘지 않는지 확인한다. 넘는다면 trap을 발생시킨다.
이제 페이지 테이블의 어떤 인덱스를 접근해야하는지 알아야 되는데, 이를 위해 앞에서 구성된 오프셋 d를 페이지 번호 p, 오프셋 d'로 자른다. 그 후에 페이지 테이블 시작 주소 + 페이지 번호 p를 통해 메인 메모리에서의 시작 주소 f를 알아내고, f에 오프셋 d'를 더하여 실제 물리적 주소로 변환하게 된다.
반효경 교수님의 운영체제 강의를 바탕으로 작성했습니다
