
2. Numeric types(숫자형)
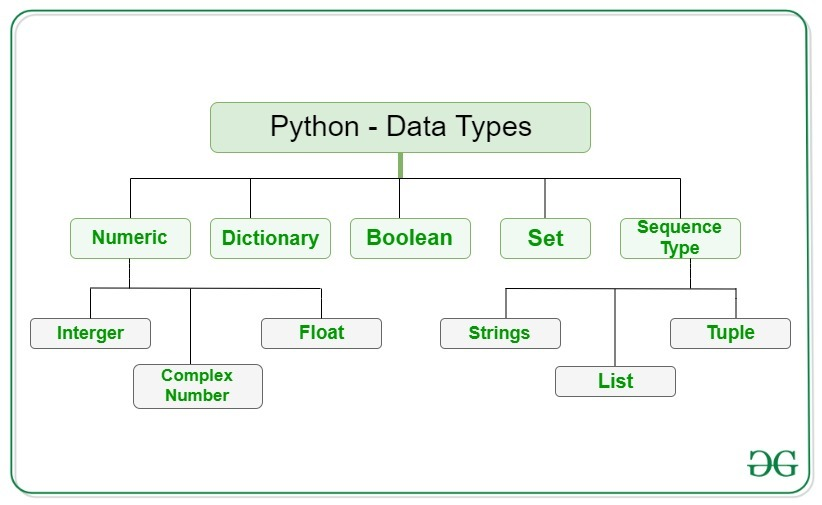
숫자형에서는 차례로 정수(integer), 실수(float) data types를 다룹니다. 위 사진의 Complex Number는 복소수로 저희에게는 필요가 없습니다. 심지어 아예 안다루는 교재도 더러 있기 때문에 여기서도 다루지 않도록 하겠습니다.
2-1. 정수형(integer types)
정수형(integer types)는 말 그대로 어떤 대상이 정수인(혹은 정수의 성질을 가지는) 것을 말합니다.
다음은 정수형(integer types)의 기본적인 특징입니다.
- 사칙연산이 가능하다
- 숫자간 비교가 가능하다
굉장히 당연한 내용입니다만, 실수는 정말 때때로 오차가 나는 경우가 있습니다.
우선 정수형(integer types)의 사칙에 대해서 알아보도록 하겠습니다.
- 덧셈( + )
Python은 덧셈을 "+" 연산자(operator)로 합니다.
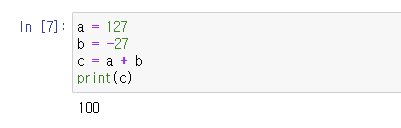
a = 127, b = -27 에서 a와 b는 변수(variable), "="는 할당 연산자(assignment operator)입니다. a와 b에 각각 127과 -27을 저장한다고 보시면 됩니다. 그렇게 되면 a와 b는 127과 -27의 값을 가지게 되는 것이죠.
그렇다면 c = a + b는 어떻게 될까요? 먼저 a와 b를 더하고, 그 값을 변수 c에 저장합니다. 그러면 c는 a와 b를 더한 값인 100을 가지게 되었겠죠.
print( )함수로 c를 출력해보면 100이 나오는 것을 확인할 수 있습니다. print( )는 괄호 안의 내용을 모니터에 출력해주는 함수인데, 변수가 들어간 경우에는 변수에 저장된 값을 출력해줍니다.
같은 느낌으로 뺄셈도 해보겠습니다.
- 뺄셈( - )
Python은 뺄셈을 "-" 연산자(operator)로 합니다.
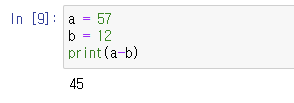
마찬가지로 a에 57을 저장하고, b에 12를 저장한 뒤에 print( )함수로 a-b의 값을 출력했습니다. 값을 출력하는 것보다 a-b를 계산하는 우선순위가 더 높아서 print(a-b)도 가능했습니다.
- 곱셈( * )
Python에서 곱셈은 "*" 연산자(operator)를 사용합니다. 이는 사실 Python뿐만 아니라 다른 언어들도 보통 *을 사용합니다.

위에서 보여드렸던 곱셈과 뺄셈의 틀에서 벗어나지 않습니다.
- 나눗셈( / )
Python에서 나눗셈은 오직 " / " 연산자(operator)만 사용합니다. Python의 나눗셈은 몇 가지 특징이 있습니다.
- " / " 연산자를 사용한다.
- 0으로 나눌 수 없다.
- 계산의 값은 묵시적으로 실수로 바뀐다.
먼저 정수를 0으로 나눠보도록 하겠습니다.

에러가 발생합니다. 0으로 나눌 때 발생하는 에러를 ZeroDivisionError라고 합니다.
0을 0으로 나누어도 같을까요?
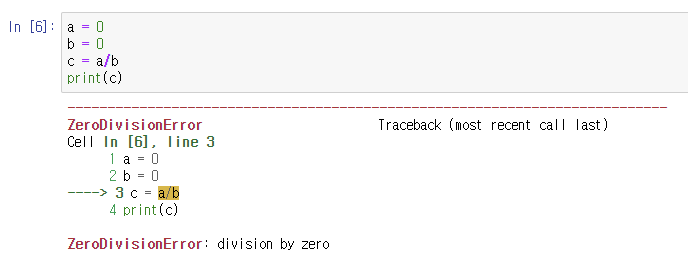
마찬가지입니다.
대신 0을 0이 아닌 다른 정수로 나누는 것은 가능합니다.

그런데 계산의 값이 뭔가 신기하지 않나요? 왜 -0.0으로 나올까요?
다음 예시를 보도록 하죠.
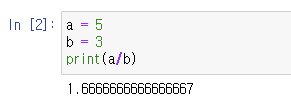
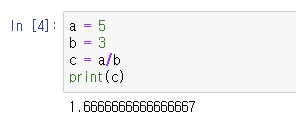
위의 예시는 당연한 것처럼 보입니다.
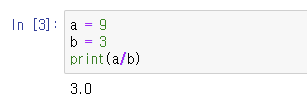
그런데 같은 정수형(integer types)끼리 나누었고, 또 나누어 떨어지는 수끼리 나누었음에도 결과값은 실수입니다.
다음과 같이 Python에서 나눗셈은 식의 계산 결과를 실수형(float types)으로 바꾸어 돌려줍니다. (type( ) 함수는 data types를 return해주는 함수입니다.)

(왜 0.0인 건 알겠는데, 왜 -0.0일까요? 그건 가능하면 나중에 정규 이외의 자료로 올려드리도록 하겠습니다. 혹시나 궁금하시다면 https://stackoverflow.com/questions/4083401/negative-zero-in-python)
- 제곱( ** )
Python은 제곱 연산자를 지원합니다. "**" 연산자(operator)를 사용합니다

주의하셔야 할 것은 제곱 연산자가 "우결합(right-to-left)"라는 것입니다. 사칙연산은 같은 연산 순서일 때{(곱셈 == 나눗셈) > (덧셈 == 뺄셈)} 왼쪽에서 오른쪽으로 계산하지만, 제곱은 오른쪽에서 왼쪽으로 계산합니다. 말이 조금 어려워졌지만, 저희가 배운 수학에서도 이런 순서는 같다는 걸 떠올리실 수 있습니다.

- 나머지( % )
아마 평소에 나머지 연산자(mod, modulo)는 볼 일이 거의 없었을 겁니다. mod라고도 부르는데 정확히는 modulo로, 컴퓨터과학에선 중요합니다. 물론 이 자체로 어려운 건 없습니다. 단순히 두 수를 나누었을 때 나머지를 계산해주는 연산자(operator)이기 때문입니다.
"%" 연산자(operator)를 사용합니다.

사실 저희가 쓰고 있는 jupyter notebook 화면은 결과값 출력을 명령하지 않아도 해주었습니다. 정말 갑자기 계산이 하고 싶어졌을 때 계산기처럼 쓰면 좋지 않을까요?
그런데 실수 계산에서는 계산기처럼 쓰는 것을 조심해야 합니다.
2-2. 실수형(float types)
실수도 사칙연산과 제곱, 나머지 연산은 물론이고 비교연산까지 모두 다 가능합니다. 그런데 앞서 정수형(integer types)의 성질이라고 하면서 "실수는 때때로 오차가 발생한다"라는 말을 했었는데요, 이게 무슨 의미일까요?
실수는 "기본적으로는 가능하지만 실수 오차로 인해 오류가 발생할 수 있다"라고 할 수 있습니다. 지금부터 실수 오차가 무엇인지 살펴보도록 하겠습니다.
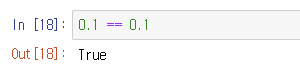
" == " 기호는 나중에 boolean data types에서 보실 수 있는데, "두 대상이 논리적으로 같은가"를 묻습니다. 0.1과 0.1은 당연히 같으니 "참", "진실"이라는 뜻에서 (==이) True를 return했고, jupyter notebook이 그 return값을 보여주네요.
그런데 이것도 같아야 되는 거 아닌가요?
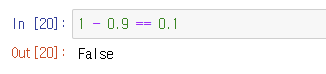
1 - 0.9 = 0.1저희가 알고 있는 상식입니다. "==" 연산자(operator)는 "논리적으로 같은가"를 확인해주니 분명 True를 return할 것이라고 예상했죠. 그런데 논리적으로 다르다고 False를 보여줍니다.
1 - 0.9 = ?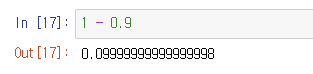
0.1이 나올 줄 알았는데, 그보다 조금 못미치는 실수가 나왔습니다. 이게 도대체 어떻게 된 일일까요?
간단히 설명하면 컴퓨터는 0과 1, 이진수(binary, binary number)를 사용한다는 걸 들어보신 적 있으실 겁니다. 우리 인간은 십진수(decimal, decimal number)를 사용하죠. 정수 부분만큼은 이진수로 십진수를 모두 표현 가능하지만, 문제는 소수 부분을 완전히 표현하는 게 불가능하다는 것이었습니다.
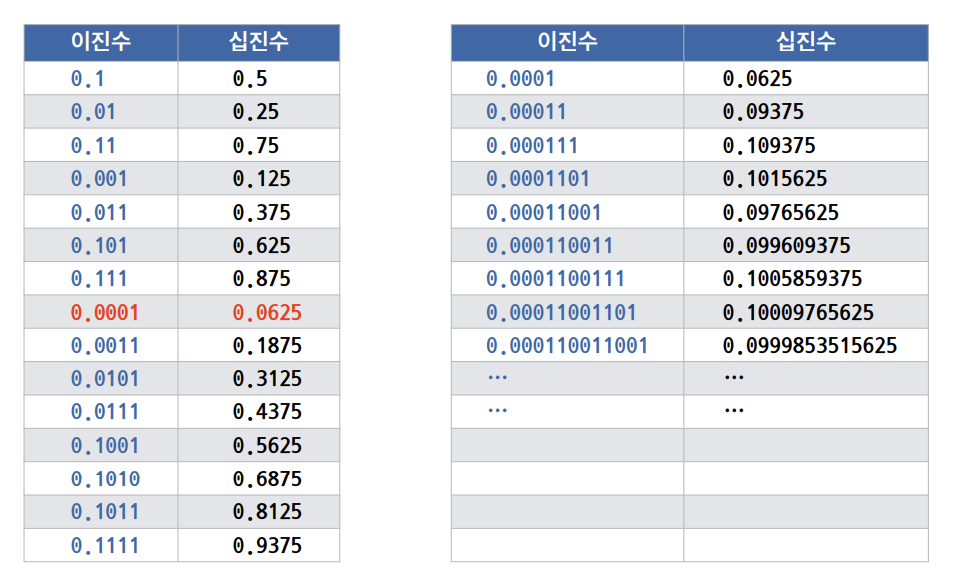
출처: 프로그래밍의 정석 : 파이썬 (도경구 교수님)사진을 보시면 아무리 0과 1을 더해보아도 0.1이 나오지 않는다는 걸 보실 수 있습니다. 우리는 이러한 오차를 실수 오차(floating point error)라고 합니다.

어느 프로그래밍 언어에서든지 실수는 표현하거나 저장할 수 있는 수의 범위가 한정되어 있습니다. 위의 사진은 실수의 밀도(floating point density)입니다. 정확한 영어 표현을 찾지 못했지만, 통상적으로 density라는 표현의 사용합니다. 그 뜻에서부터 한정된 실수들이 어떻게 밀집되어 있는지 나타내죠. 왼쪽으로 갈수록 촘촘해지고, 오른쪽으로 갈수록 널널해집니다.
- 매우 큰 실수일수록 연산에 오차가 발생하기 쉽다는 사실을 기억해주세요.
.
.
.
실수의 범위가 구체적으로 어떻게 정의되어 있는지 궁금하신 분들을 위해 추가 자료를 제작하고 있습니다... 되려 추가 자료 구성시간때문에 메인 업로드가 늦는 점 죄송합니다...
