[자료구조] 이진트리 (feat. python)

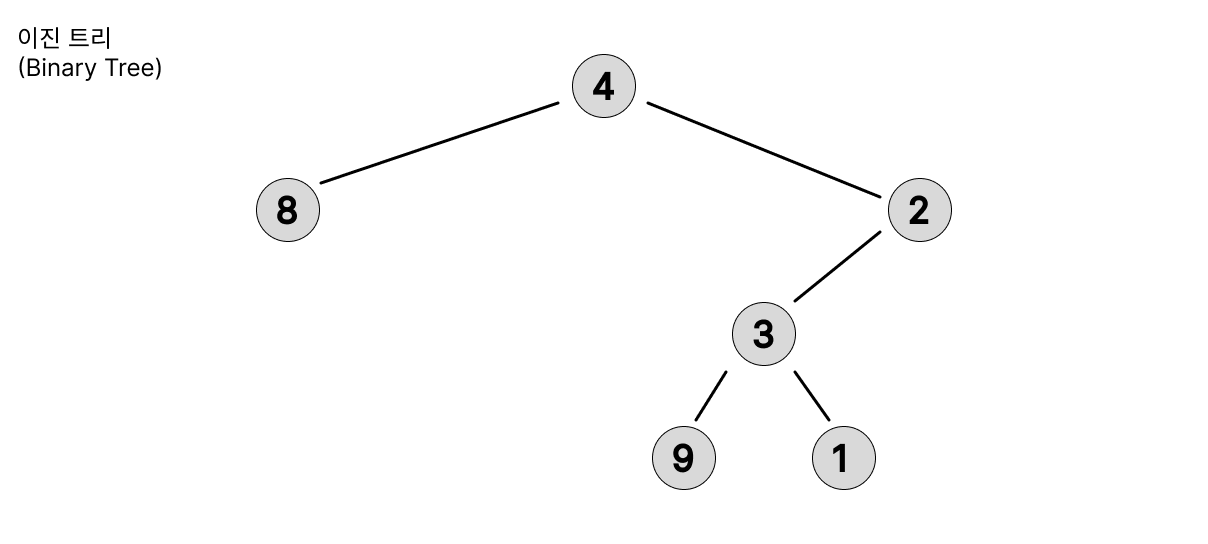
Binary Tree

트리 구조의 형태를 띄고 있으며, 일반적으로 0~2의 자식 노드를 가지고 있는 것이 특징이다.

용어:

• Root Node: 제일 상위에 있는 부모 노드
• Leaf Node: 제일 하단에 있는 자식 노드
• Node: Root 또는 Leaf가 아닌 내부 노드
• Link or Edge: Node와 Node를 잇는 간선
• Key: 노드가 가지고 있는 값
• $h$: 트리의 높이
• path: $x_1$ ~ $x_2$ 노드까지 최단 경로 Edge의 갯수

Binary Tree의 종류

일반 이진 트리(Binary Tree)

• 가장 기본적인 이진 트리를 칭하고, 0~2개의 Children Node를 가지고 있다.
• 구조에 대한 제약이 없다.
  
  
  

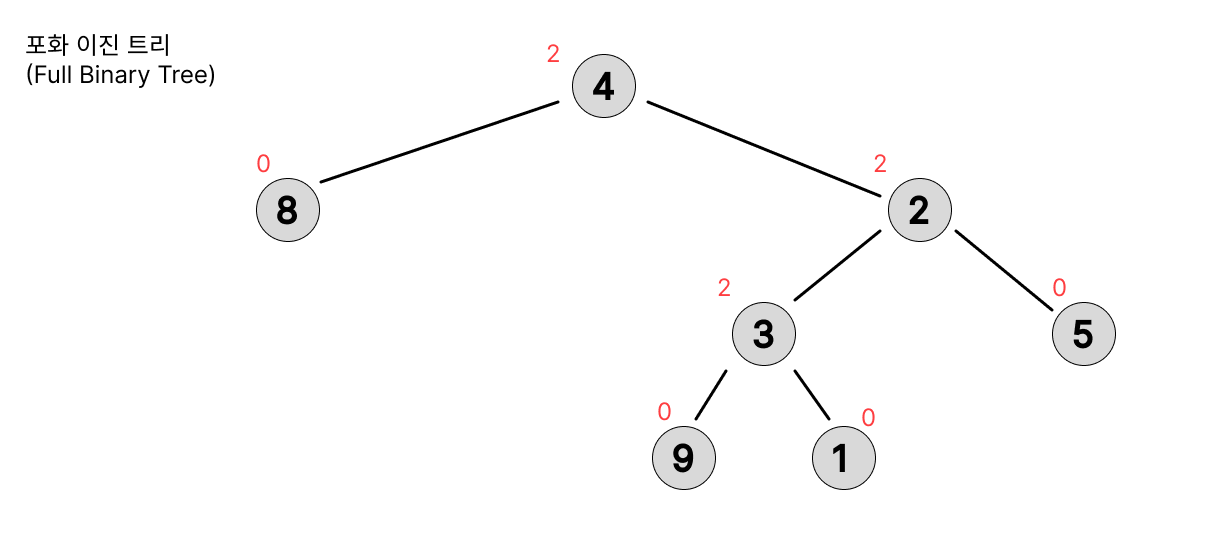
포화 이진 트리(Full Binart Tree)

• 모든 노드가 0 or 2 개의 Children Node를 가진다.
• 모든 내부에 있는 Node는 정확히 두 개의 Children Node를 가진다.
• 서로 다른 Leaf Node는 동일한 Lv가 아니여도 된다.
  
  
  

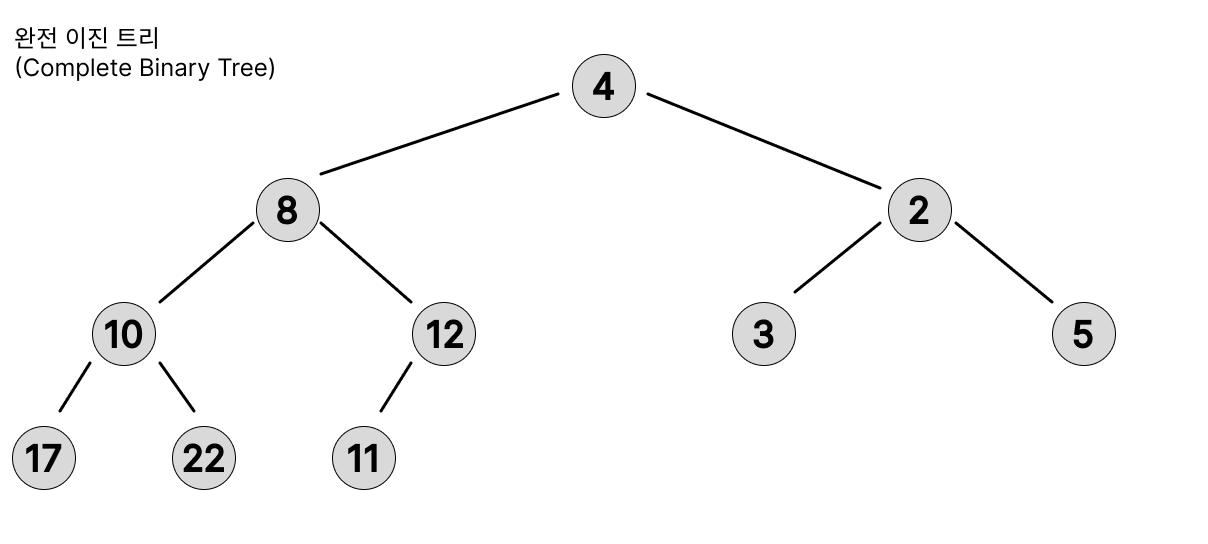
완전 이진 트리(Complete Binary Tree)

• 마지막 Lv을 제외한 모든 Lv이 완전히 채워져 있다.
• 마지막 Lv은 왼쪽부터 채워져야 하되, 가득 차있을 필요는 없다.
  
  
  

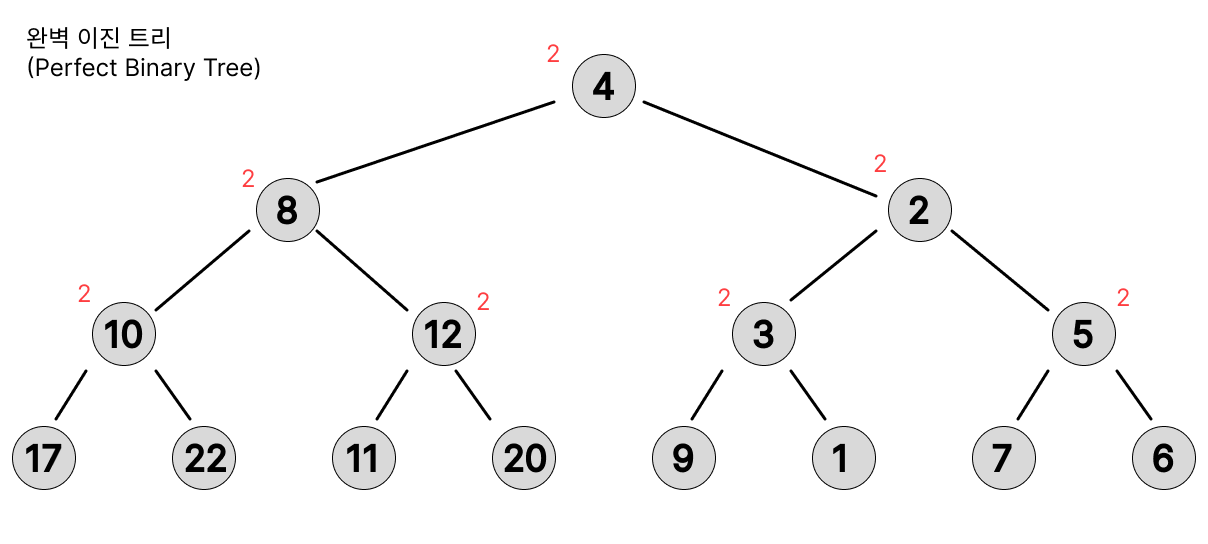
완벽 이진 트리(Perfect Binary Tree)

• Leaf Node를 제외한 모든 Node는 정확히 두 개의 Children Node를 가진다.
• 서로 다른 Leaf Node는 모두 동일한 Lv에 해당해야 한다.
• $N$이 노드의 총 갯수라고 하면 총 갯수 수식은 아래와 같다.
  수식: $N = 2^{h+1} - 1$
  
  
  

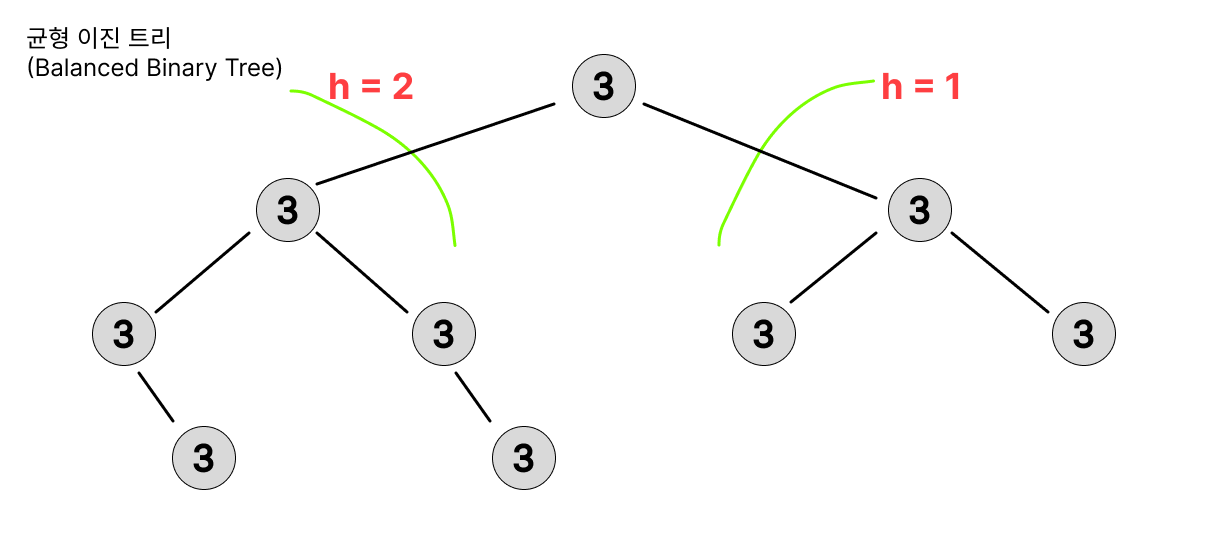
균형 이진 트리(Balanced Binary Tree)

• 모든 노드에서 Left-SubTree($LH$)와 Right-SubTree($RH$)의 높이 차이가 최대 1이다.
  수식: $|LH - RH| = 0$ or $|LH - RH| = 1$
• 효율적인 탐색, 삽입, 삭제 연산을 보장한다.
• ex) AVL Tree, Red-Black Tree 가 균형 이진 트리에 해당한다.
  $\rightarrow$ 추후에 다룰 예정