📌 그리디 알고리즘(Greedy) 이란?
그리디 알고리즘이란 말 그대로 greedy(탐욕스러운) 알고리즘이다.
즉, 각 단계에서 지금 당장 가질 수 있는 최선의 선택을 해 최고의 이익을 따라가는 알고리즘을 의미한다.
아래 예시를 보면 쉽게 이해할 수 있을 것이다.
위와 같은 트리에서 루트 노드에서부터 내려가며 최대합을 구하는 문제가 주어졌을 때 그리디 알고리즘을 적용해보자.
1. 루트 노드인 7에서 3과 12 중 최선의 선택은 12이므로 12 선택.
2. 12에서 5와 6 중 최선의 선택은 6이므로 6 선택.
=> 7 + 12 + 6 = 25가 결과값이 된다.
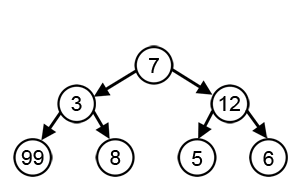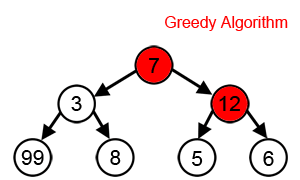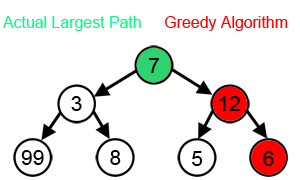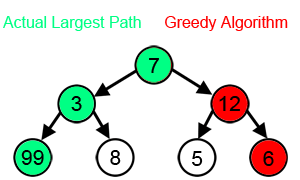
하지만 정답은 25가 아닌 7 + 3 + 99 = 109다.
위 예시에서 볼 수 있듯이 그리디 알고리즘은 모든 경우 최적해를 보장하지 못한다.
최적해를 보장하지 못하므로 그리디 알고리즘은 잘못된 것이 아니냐는 생각이 들 수도 있지만 또 그렇지만은 않다.
각 단계에서 최선의 선택을 하기 때문에 간단하고 빠르다는 장점이 있고 이로인해 드물게 최적해를 결과로 내는 경우도 있다.
즉, 합리적인 시간 내로 최적에 가까운 해답을 찾을 수 있다는 점에서 유용한 알고리즘이다.
그리디 알고리즘을 통해 최적해를 보장받기 위해선 조건이 필요하다.
📌 최적해 보장 조건
그리디 알고리즘을 적용해 최적해를 보장받으려면 다음 세가지 조건이 성립해야 한다.
- 탐욕적 선택 속성(Greedy Choice Property)
매 단계에서 내리는 현재의 선택이 이후의 선택에 영향을 미치지 않고, 최적의 결과를 보장해야 한다.
즉, 각 단계에서 최선이라고 판단되는 선택을 했을 때도 여전히 전체 문제의 최적해로 이어질 수 있어야 한다. - 최적 부분 구조(Optimal Substructure)
문제를 여러 하위 문제로 나누었을 때, 각 하위 문제의 최적화를 결합하면 전체 문제의 최적해를 구할 수 있어야 한다. - 단항 선택 조건(Unary Choice Condition)
각 단계에서 가능한 선택지가 여러 개 있을 경우, 그 중 하나를 선택해도 이후 단계의 선택에 영향을 미치지 않아야 한다.
즉, 매 순간의 선택이 독립적이어야 하며, 선택의 결과가 최적해를 방해하지 않아야 한다.
동적계획법(DP)과의 차이점
위 조건 중 하나인 최적 부분 구조에서 빼놓을 수 없는 알고리즘 기법인 동적계획법(DP)과의 차이점은 무엇일까.
두 기법에는 의사결정 방식의 차이가 있다.
DP는 모든 가능한 선택을 고려하며 최적의 해를 보장하는 포괄적인 접근 방식이지만 그리디 알고리즘은 현재 가장 좋은 선택을 반복적으로 수행하며 빠르게 해를 구한다.
또한 DP는 메모리를 사용하여 중복 계산을 방지하지만, 공간 복잡도가 높아질 수 있다.
반대로 그리디 알고리즘은 저장 공간을 사용하지 않으므로 더 간단하고 효율적일 때가 많다.
그렇다면 언제 어떤 기법을 사용해 문제를 해결해야 할까?
DP는 하위 문제 간의 관계가 복잡하고 중복되는 계산이 많은 문제에 적합하고(ex. 0/1 배낭 문제),
그리디 알고리즘은 선택이 독립적이고 현재 최선의 선택이 전체 최적해로 이어지는 경우에 적합하다(ex. 최소 동전 문제).
