백트래킹이란?

백트래킹(BackTracking)은 탐색 알고리즘 중 하나로,
탐색을 통해 정답을 찾아가다 가능성이 없다고 판단하면 해당 분기에 대한 탐색을 중단하고 되돌아가서 정답을 다시 찾아가는 기법이다.

더이상 탐색할 필요가 없는 상태를 제외(가지치기)시키며 탐색을 진행하기 때문에 탐색 공간을 줄여 문제를 효율적으로 해결할 수 있도록 한다.

백트래킹 또한 모든 경우에 수에서 조건을 만족하는 경우를 탐색하는 것이기 때문에 완전탐색기법인 DFS와 BFS로 구현이 가능하다.
즉, DFS와 BFS에서 한정 조건을 걸어 유망하지 않은 시도를 걸러내는 것이 백트래킹이라고 볼 수 있다.

하지만 탐색을 진행하다 조건에 부합하지 않으면 되돌아가는 백트래킹 특성 상 BFS보다는 DFS의 구현이 더 편리하다.

---

N-Queen

백트래킹으로 해결할 수 있는 대표적인 문제인 N-Queen을 통해 동작 과정을 이해해보자.

N-Queen 문제는 N x N 체스보드에 N개의 퀸을 배치하는 문제다.
이 때 어떤 퀸도 다른 퀸에 의해서 잡아먹히지 않도록 배치해야 한다.
(퀸은 좌우, 상하, 대각선 모든 방향으로 이동할 수 있다.)

N이 4로 주어졌다고 가정하고 백트래킹을 적용해보자.

퀸이 좌우로 움직일 수 있으므로 각 행마다 퀸을 하나씩 배치한다.
먼저 (0, 0)에 퀸을 배치한다.

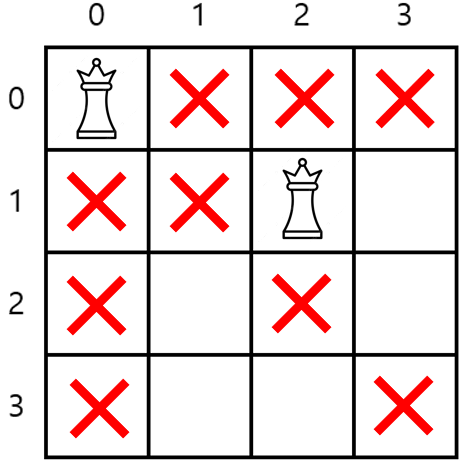
퀸은 상하, 대각선으로도 움직일 수 있기 때문에 퀸은 (1, 2), (1, 3)에 위치할 수 있다.
먼저 가까운 (1, 2)에 퀸을 놓자.

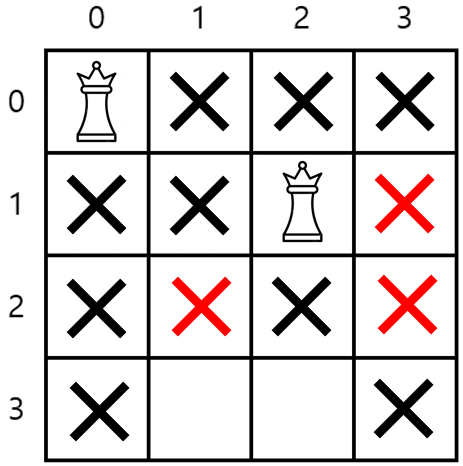
2행에 퀸을 배치하려고 보니 가능한 칸이 없다.
N개의 퀸을 놓을 수 없다는 뜻이다.
탐색을 중단하고 다시 1행으로 돌아간다.(가지치기)

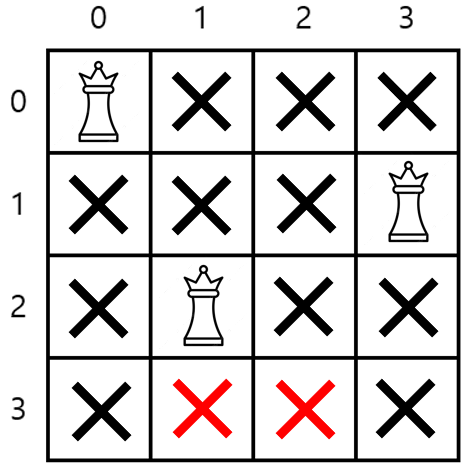
(1, 3)에 퀸을 배치하면 (2, 1)에 퀸을 배치할 수 있다.
하지만 3행에 퀸을 배치할 수 없게 되므로 탐색을 중단하고 0행으로 돌아간다.

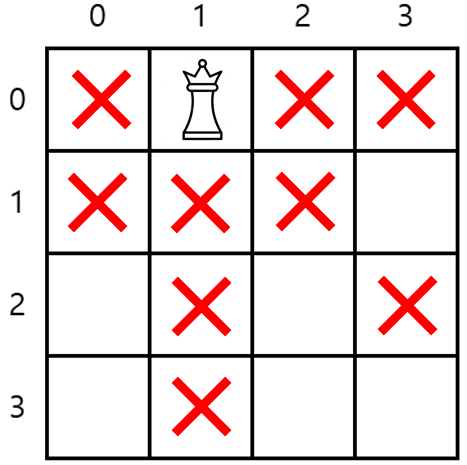
(0, 1)에 퀸을 배치하고 탐색을 이어간다.

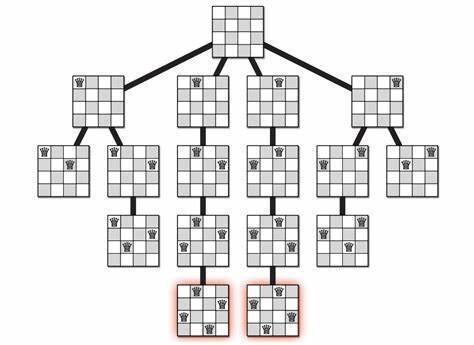
4 x 4 체스판에 4개의 퀸을 배치할 수 있는 경우의 수는 2가지가 있다.

완전탐색 기법인 DFS의 경우의 수인 256(4 x 4 x 4 x 4)보다 훨씬 적은 수의 경우를 탐색한 것을 확인할 수 있다.