분리집합이란?

집합은 어떤 명확한 조건을 만족시키는 서로 다른 대상들의 모임이다.

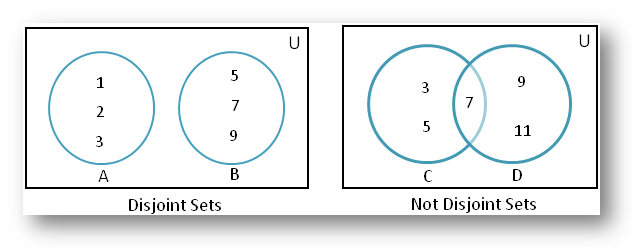
분리집합은 말 그대로 분리된 집합이다.
다른 말로 서로소 집합이라고도 하며 각각의 집합이 공통 원소를 가지고 있지 않은 집합을 말한다.

전체 집합 U에서 분리 집합 A, B는 다음과 같은 조건을 만족한다.

• A, B는 U의 부분 집합이다.
• A, B는 공통 원소를 가지지 않는다.
• A, B의 합집합은 전체 집합

그렇다면 분리집합을 왜 사용할까?

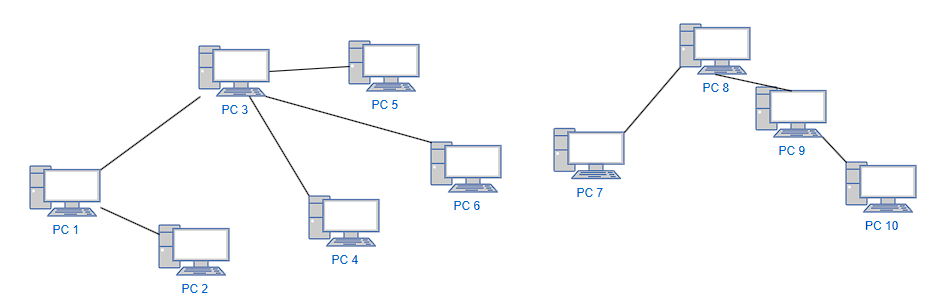
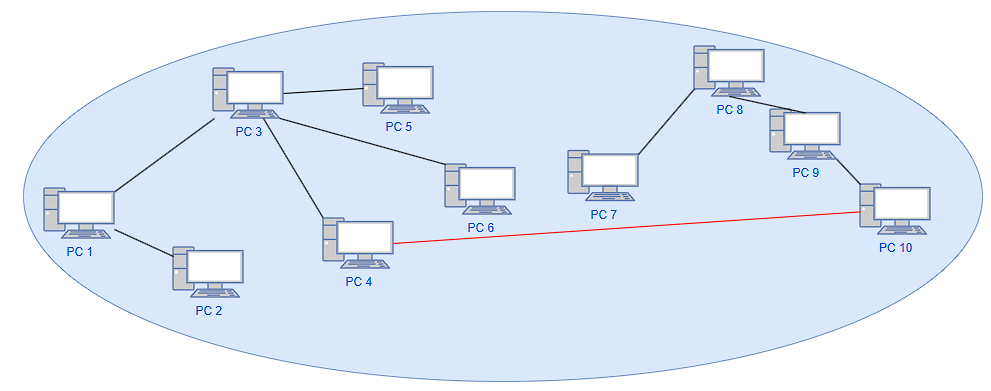
다음과 같이 구성된 네트워크에서 두 PC가 연결되었는지 확인하는 문제가 있다.

PC2와 PC7이 연결되었는지 확인해보자.
PC 연결 정보를 그래프로 나타낸 후 그래프 탐색(DFS, BFS)을 한다면 연결되지 않았다는 것을 간단하게 확인할 수 있다.

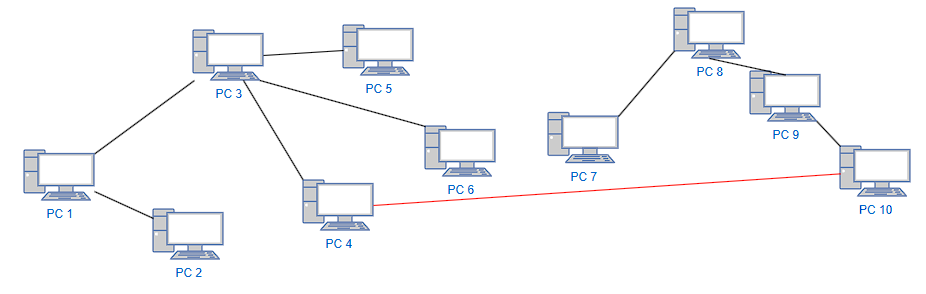
하지만 다음과 같이 새로운 연결이 생겼을 때 두 PC가 연결되었는 지 확인하기 위해 다시 그래프 탐색을 진행해야 한다.

위의 예시는 간단하지만 PC의 개수가 많아진다면 새로운 연결이 생겨날 때마다 모든 PC에 대해 그래프 탐색이 진행되어야 하므로 시간이 굉장히 오래 걸릴 것이다.

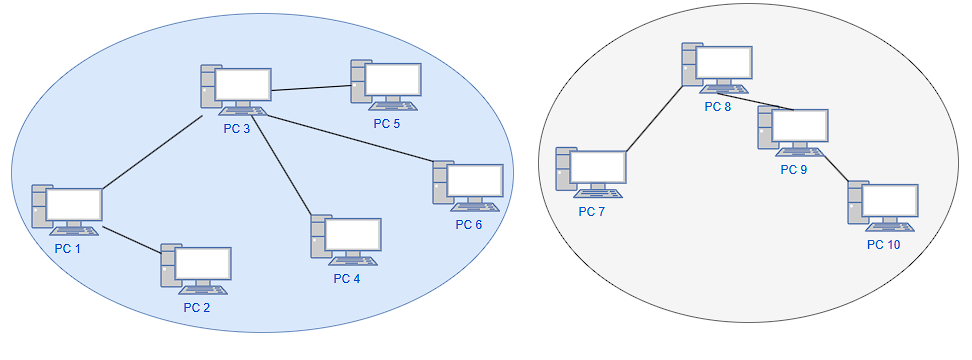
PC의 연결 구조를 그래프의 형태가 아닌 집합을 통해 표현한다면 소요되는 시간을 줄일 수 있다.
PC2와 PC7는 다른 집합에 속해 있으므로 두 PC는 연결되어 있지 않다는 것을 쉽게 확인할 수 있다.

새로운 연결이 생겼을 땐 두 집합을 합침으로써 PC 연결 관계를 갱신할 수 있다.
새로 탐색을 진행할 필요가 없다.

Union-Find

위 설명을 통해 분리집합은 알고리즘보단 자료구조라는 것을 느꼈을 것이다.

Union-Find는 이러한 분리집합을 구현한 알고리즘이다.
각 집합은 트리의 형태로 표현되며 트리의 루트 노드가 집합의 대표값이 된다.
Union-Find은 다음 3가지 연산을 통해 구현된다.

• make_set(x)
  초기화 작업으로 x를 유일한 원소로 하는 새로운 집합을 만든다.
• find(x)
  x가 속한 집합의 대표 노드(루트)를 찾는 연산으로 x가 어떤 집합에 속해 있는지 찾는다.
• union(x, y)
  x가 속한 집합과 y가 속한 집합을 하나로 합친다.

코드 구현

class DisjointSet:
    def __init__(self, n):
        self.parent = [i for i in range(n)]  # 부모를 자기 자신으로 초기화
        self.rank = [1] * n  # 트리의 랭크를 1로 초기화

    def find(self, x):
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])  # 경로 압축
        return self.parent[x]

    def union(self, x, y):
        rootX = self.find(x)
        rootY = self.find(y)

        if rootX != rootY:
            if self.rank[rootX] > self.rank[rootY]:
                self.parent[rootY] = rootX
            elif self.rank[rootX] < self.rank[rootY]:
                self.parent[rootX] = rootY
            else:
                self.parent[rootY] = rootX
                self.rank[rootX] += 1