극댓값 찾기

1차원의 경우

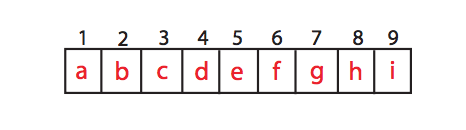
b ≥ a이고 b ≥ c 이면 2번 위치가 극댓값이다. i ≥ h 이면 9번 위치가 극댓값이다.

간단한 알고리즘을 살펴 보겠습니다.

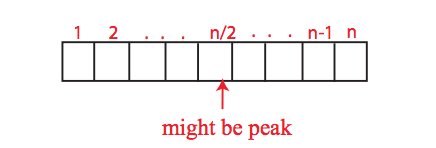
극댓값이 중간에 있다고 가정하고 숫자는 왼쪽에서 중간으로 증가하고 감소하기 시작합니다. 여기서 알고리즘은 극댓값을 찾기 위해 n / 2 개의 요소를 조사해야합니다.

다시 극댓값이 오른쪽 끝까지 있다고 가정 해 보겠습니다. 따라서 왼쪽에서 오른쪽 끝까지 극댓값 검색을 시작하면 극댓값을 찾기 위해 n 개의 요소를 볼 수 있습니다.

따라서 최악의 시나리오에서 복잡도는 Θ (n)이됩니다. 즉, 배열의 모든 요소를 살펴 봐야합니다. 그래서 우리가 여기서 실제로 말하는 것은 알고리즘의 점근 적 복잡도가 선형이라는 것입니다.

분할 정복

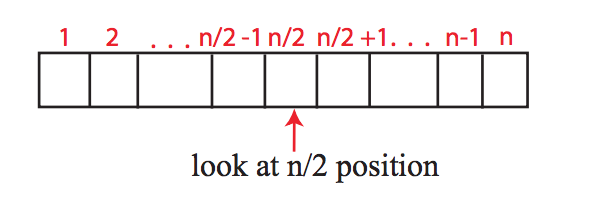
이것은 분할 정복 알고리즘입니다. 우리는 주로 n / 2 위치를 볼 것입니다.

• a[n/2] < a[n/2 - 1] 이면 왼쪽 절반인 1부터 n/2-1까지 보고 극댓값을 찾는다.
• 그게 아니고 a[n/2] < a[n/2 + 1] 이면 오른쪽 절반인 n/2 + 1부터 n까지 보고 극댓값을 찾는다.
• 그것도 아니면 n/2 위치가 극댓값이다.

이 경우 복잡도는?

Θ(i)들을 합하려면, 모든 경우에 적용되는 상수를 찾아야 한다. n = 1000000인 경우, 파이썬에서 Θ(n) 알고리즘을 실행하는 데 13초가 걸린다. Θ(log n) 알고리즘은 0.001초밖에 걸리지 않는다.

2차원의 경우

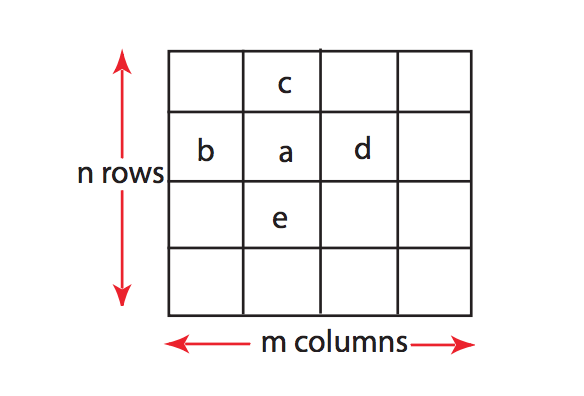
a ≥ b, a ≥ d, a ≥ c, a ≥ e이면 a는 2차원 극댓값이다.

탐욕 상승 알고리즘이라는 간단한 알고리즘 부터 시작하겠습니다.

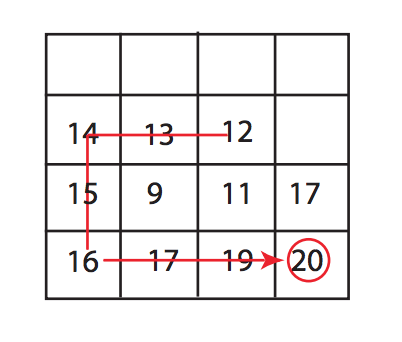
탐욕 상승 알고리즘에서는 시작할 곳을 선택해야합니다.

그래서 우리가 12로 시작하고 싶다고 말하면, 우리는 남은 것을 찾을 것입니다. 그리고 그것이보다 크다면 우리는 그 방향을 따를 것입니다. 그렇지 않다면 다른 방향으로 가고있는 것입니다. 따라서이 경우 12, 13, 14, 15, 16, 17,19, 20으로 이동합니다. 그리고 피크를 찾을 수 있습니다. 이 알고리즘에서 피크를 찾으려고하면 요소의 절반 부분을 만져야 할 수도 있고 행렬에있는 요소의 모든 부분을 만져야 할 수도 있습니다. 따라서 알고리즘의 최악의 경우 분석을 시도하면 Θ (nm)가 될 것입니다. 여기서 n은 행 수이고 m은 열 수입니다. n = m 인 경우 최악의 복잡도는 Θ (n²)입니다.

이제 1차원 분할 정복을 2차원으로 확장하여 복잡도를 개선해 보겠습니다.

시도 # 1

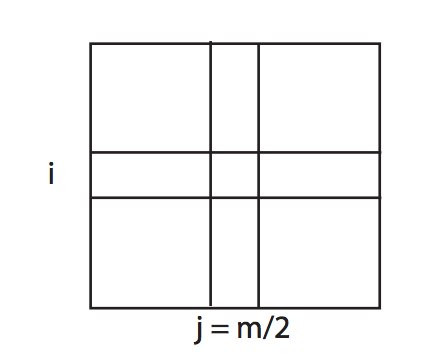
• 중앙 열 j = m/2을 선택한다.
• (i, j)에서 1차원 극댓값을 발견한다.
• (i, j)를 시작 지점으로 하여 i행에서 1차원 극댓값을 찾는다.

문제는 2차원 극댓값이 i행에 존재하지 않을 수도 있다.

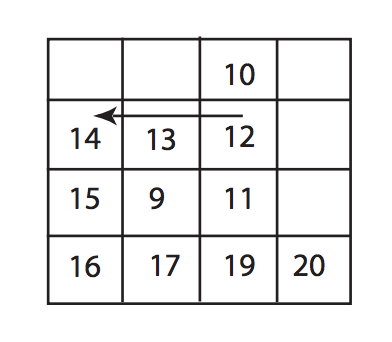
2차원 극댓값이 아닌 14를 찾는 걸로 끝남.

예를 살펴 보겠습니다.

왼쪽에서 세 번째 열을 가운데로 선택하겠습니다. 우리는 피크를 찾기 시작하고 12를 피크로 반환했습니다. 12를 둘러싼 값이 12보다 작기 때문에 19가 실제 피크 임에도 불구하고 12를 피크로 반환하는 것이 가능합니다. 그래서 저는 12를 선택으로 선택하고 피크를 찾기 시작합니다. 12가있는 행에. 행을 보면 피크는 14에 있습니다. 알고리즘은 14를 매트릭스의 피크로 반환합니다. 14가 1D 케이스에서 피크라는 것은 사실이지만 2D 14의 관점에서 보면 피크가 아니므로 알고리즘이 올바르지 않습니다. 이것은 효율적인 알고리즘처럼 보이지만 작동하지 않습니다.

따라서 이 문제를 해결할 마지막 알고리즘은 다음과 같습니다.

시도 # 2

중앙 열 j = m/2을 선택한다.

• (i, j)에서 j열의 최댓값을 찾는다.
• (i, j − 1), (i, j), (i, j + 1)를 비교한다.
• (i, j − 1) > (i, j)이면 왼쪽 열을 선택한다.
• 오른쪽도 똑같이 진행한다.
• 두 조건 모두 만족하지 않으면, (i, j)가 2차원 극댓값이다.
• 열 개수가 절반으로 줄어든 새로운 문제를 푼다.
• 열이 1개 남으면, 최댓값을 찾고 끝난다.

시도 #2 예시

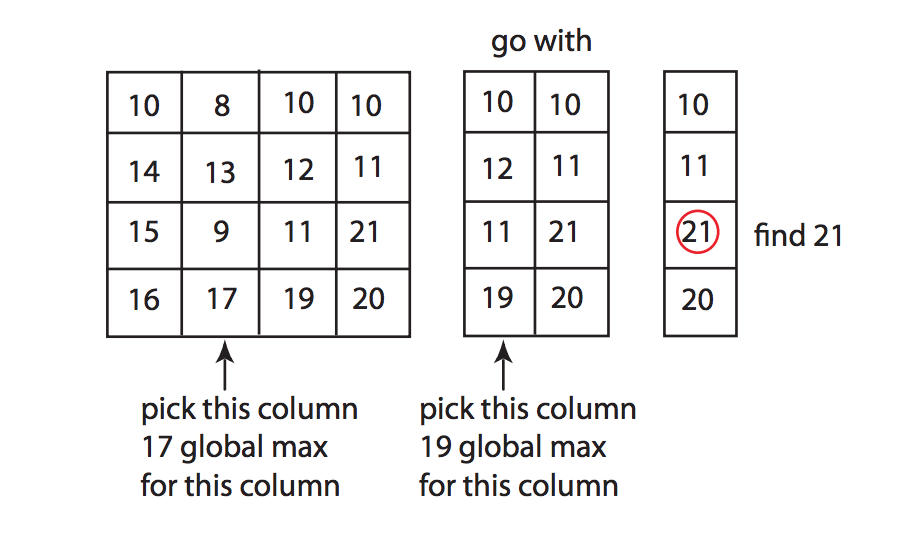
따라서 이 재귀 알고리즘에 대한 T (n, m)의 재귀 관계는 다음과 같습니다.

T (n, m) = T (n, m / 2) + Θ (n)

n은 행의 수이고 m은 열의 수이기 때문에 이것이 방정식 인 이유는 무엇입니까? 한 경우에 우리는 m / 2 인 절반 수의 열로 나누고 전역 최대 값을 찾기 위해 다음과 같이 할 것입니다. Θ (n) 작업을 수행합니다.

그래서 우리는 위의 방정식을 취하고 그것을 확장하여 결국 우리는 최상의 경우에 도달 할 것입니다.

T (n, 1) = Θ (n).

따라서 방정식을 다음과 같이 쓸 수도 있습니다.

T (n, m) = Θ (n) + …… + Θ (n) [이것은 위 방정식의 확장 된 형태입니다]

우리는 그것을 log m 번 확장 할 것입니다. 따라서 알고리즘의 복잡성은 Θ (n log m)입니다.