합병정렬 & 삽입정렬

합병 정렬 (Merge Sort)

합병 정렬은 분할정복(Divide and Conquer) 알고리즘의 일종이다. 분할정복 알고리즘이란 문제를 나눌 수 없을 때까지 나눈 다음, 나누어진 각각의 문제들을 풀면서 다시 합병을 하여 문제의 답을 얻는 알고리즘이다.

합병 정렬의 전반적인 순서는 다음과 같다

1. 반으로 분할 (배열의 가장 최소단위인 1까지)
2. 정렬

위 과정을 정렬이 완료될때까지 계속 반복을 해준다.

합병 정렬 유튜브

다음 숫자들을 오름차순으로 정렬하는 프로그램을 작성하세요.
[27, 15, 10, 25, 30, 13, 19, 21]

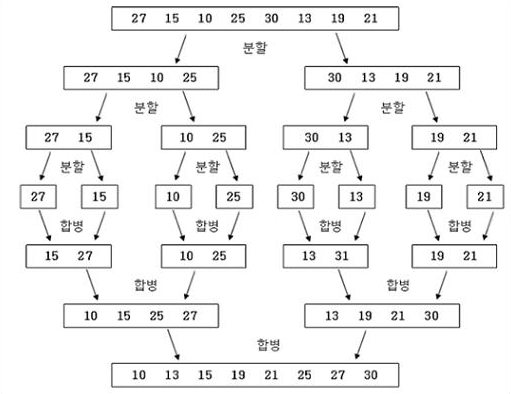
실제로 각 배열들이 정렬되는 과정은 다음과 같다

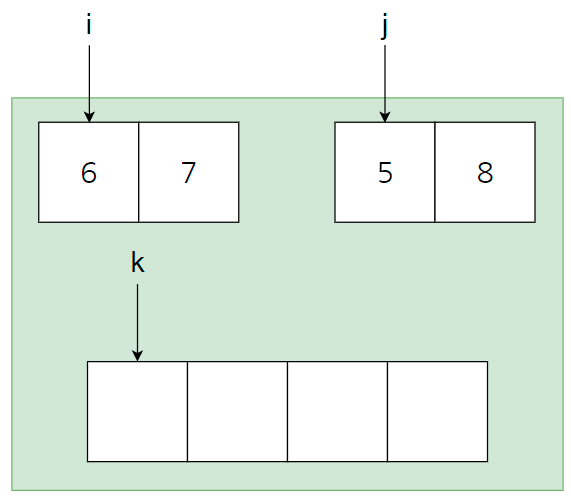
i = 정렬된 왼쪽 배열의 인덱스
j = 정렬된 오른쪽 배열의 인덱스
k = 합칠 배열의 인덱스

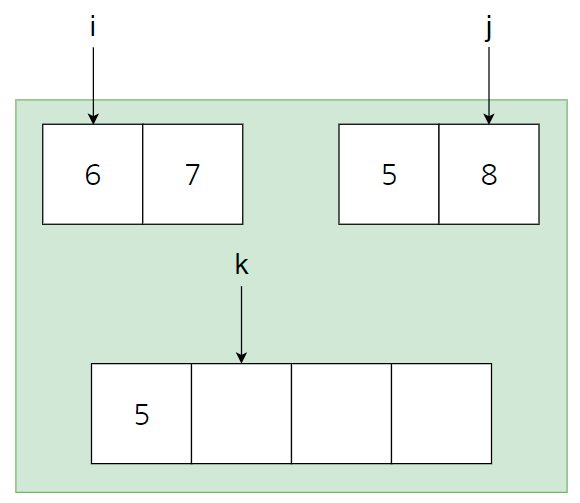
• 오른쪽 배열의 첫번째 인덱스의 숫자 5가 가장 작은 값이 되므로 5를 합칠 배열의 인덱스에 넣어준다.
• 오른쪽 배열의 인덱스인 j를 1 증가시킨다.
• 합칠 배열의 인덱스인 k를 1 증가시킨다.

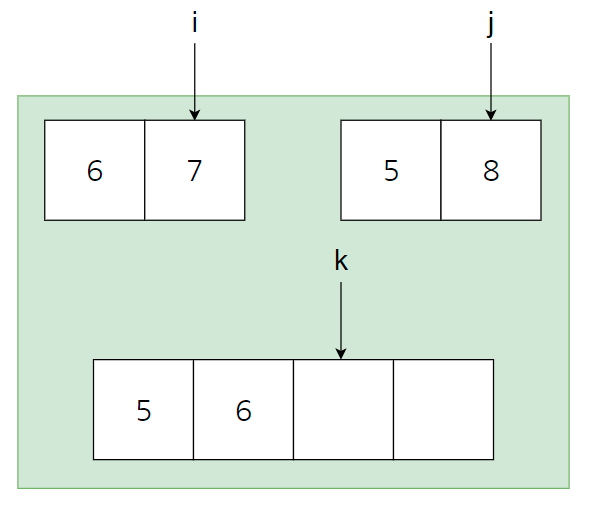
• 남은 배열중에서 왼쪽 배열의 인덱스의 숫자 6이 가장 작은 값이 되므로 6을 합칠 배열의 인덱스에 저장한다.
• 왼쪽 배열의 인덱스인 i를 1 증가시킨다
• 합칠 배열의 인덱스인 k를 1 증가시킨다.

코드

arr = [27, 15, 10, 25, 30, 13, 19, 21]

def mergeSort(arr): 

    # 종료 조건: 정렬할 리스트의 자료 개수가 한 개 이하이면 정렬할 필요가 없음
    if len(arr) <=  1:
        return 
	
    # 배열은 반으로 나눠 각각 합병 정렬을 호출하는 과정 
    mid = len(arr)//2 # 배열의 가운데 인덱스를 구한다

    # 가운데 인덱스를 기준으로 왼쪽, 오른쪽 배열을 슬라이싱하여 나눈다
    left_array = arr[:mid] 
    right_array = arr[mid:] 

    mergeSort(left_array) # 왼쪽 배열 정렬
    mergeSort(right_array) # 오른쪽 배열 정렬 

    # 왼쪽, 오른쪽 배열을 합치는 과정
    i = j = k = 0
        
    # 왼쪽 오른쪽 배열의 각 요소들을 비교하면서 arr[] 배열에 정렬하여 넣어준다
    while i < len(left_array) and j < len(right_array):           

        # 왼쪽 배열의 요소가 더 클 때
        if left_array[i] < right_array[j]: 
            arr[k] = left_array[i] 
            i+= 1

        # 오른쪽 배열의 요소가 더 클 때
        else: 
            arr[k] = right_array[j] 
            j+= 1
        k+= 1
        
    # 왼쪽 배열의 요소가 없을 때 
    while i < len(left_array): 
        arr[k] = left_array[i] 
        i+= 1
        k+= 1
        
    # 오른쪽 배열의 요소가 없을 때       
    while j < len(right_array): 
        arr[k] = right_array[j] 
        j+= 1
        k+= 1

삽입 정렬(Insertion Sort)

정렬이 되어있지 않은 배열의 모든 요소를 앞에서부터 정렬된 배열과 비교하여 들어갈 위치를 찾고, 그 위치에 삽입하여 정렬하는 방식이다. 삽입 정렬을 추가적인 배열을 사용하지 않고 입력된 배열을 정렬된 부분과 정렬되지 않은 부분으로 나누어서 사용한다.

삽입 정렬 유튜브

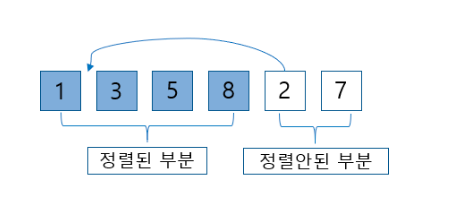
삽입 정렬을 필요할 때에 한해서만 삽입 연산을 진행하기 때문에 거의 정렬된 상태의 데이터에서 삽입 정렬 알고리즘을 적용할 경우 그 어떤 정렬 알고리즘보다 빠르다는 특성을 가지고 있다.

def insertionSort(arr): 
  
    # 두 번째 배열의 요소부터 시작한다
    for i in range(1, len(arr)): 
        
        # 삽입할 숫자
        key = arr[i]

        # j = 삽입할 숫자의 이전 인덱스
        j = i-1
        while j >= 0 and key < arr[j] :
                # 삽입할 숫자보다 배열의 요소가 더 크면 오른쪽으로 한칸씩 밀어준다 
                arr[j + 1] = arr[j] 
                j -= 1
        # 적절한 위치에 넣어준다 
        arr[j + 1] = key   
    
    print(arr)

참고사이트

나동빈