Dijkstra(다익스트라)

그래프에서 특정 정점에서 목적지까지 최단 경로를 구하는 알고리즘

대표적인 최단 경로 알고리즘중 하나가 다익스트라 알고리즘이다.

BFS,DFS 를 사용하는 경우(가중치가 같을경우)

그래프의 간선 가중치가 모두 같을 때 적합하다.

예를 들어 2차원배열에서 입력이 주어진 상태로 시작점에서 도착점까지의 최단경로 구할때 어떤 위치에서 다음위치까지 거리가 같기때문에 BFS,DFS 를 사용해서 최단경로를 구하는게 대부분이다.

가중치가 다를땐 어떤방식으로 해야할까요?

이번에 배워볼 다익스트라 알고리즘으로 가중치가 다를때 구하는게 적합하다.

다익스트라 알고리즘이란?

• Edsger Wybe Dijkstra가 고안한 최단경로 알고리즘.
• 우선순위 큐를 이용하려 만들 수 있다.
• 시간복잡도는 V가 정점의 수, E가 간선의 수일때 시간복잡도는 Elog V 가 된다.

다익스트라 알고리즘 순서

1. 먼저 시작점을 제외한 나머지 정점을 다 무한값으로 초기화 해준다.

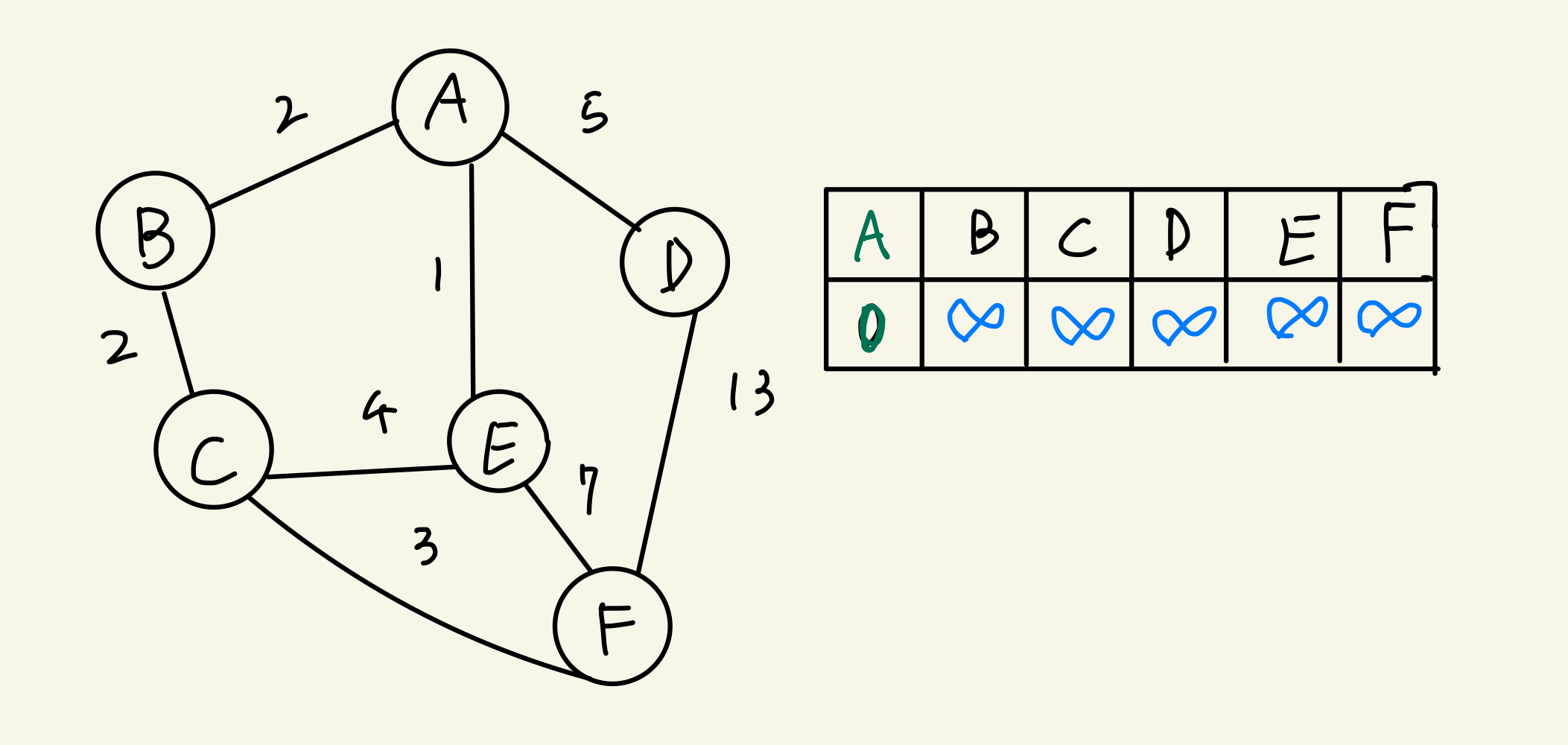
2. 시작점 기준으로 시작점에서 갈 수 있는 정점을 찾고 값을 재할당 해 준다.

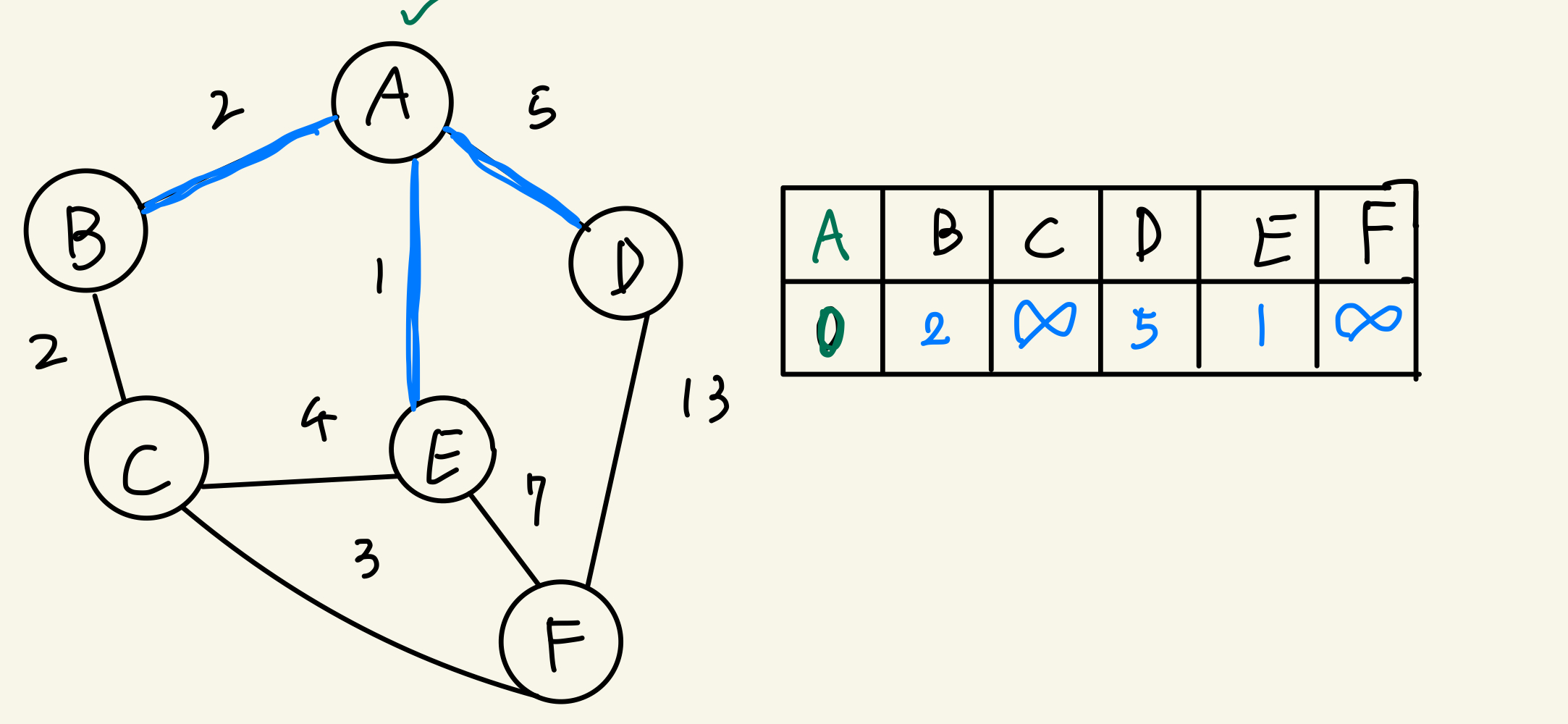
3. 여기서 설정된 정점중에 최단거리가 제일 짧은 정점을 선택해 준다. 선택후 해당 정점(E)에서 또 뻗어나간 간선을 통해서 정점 값을 재할당 해 준다.

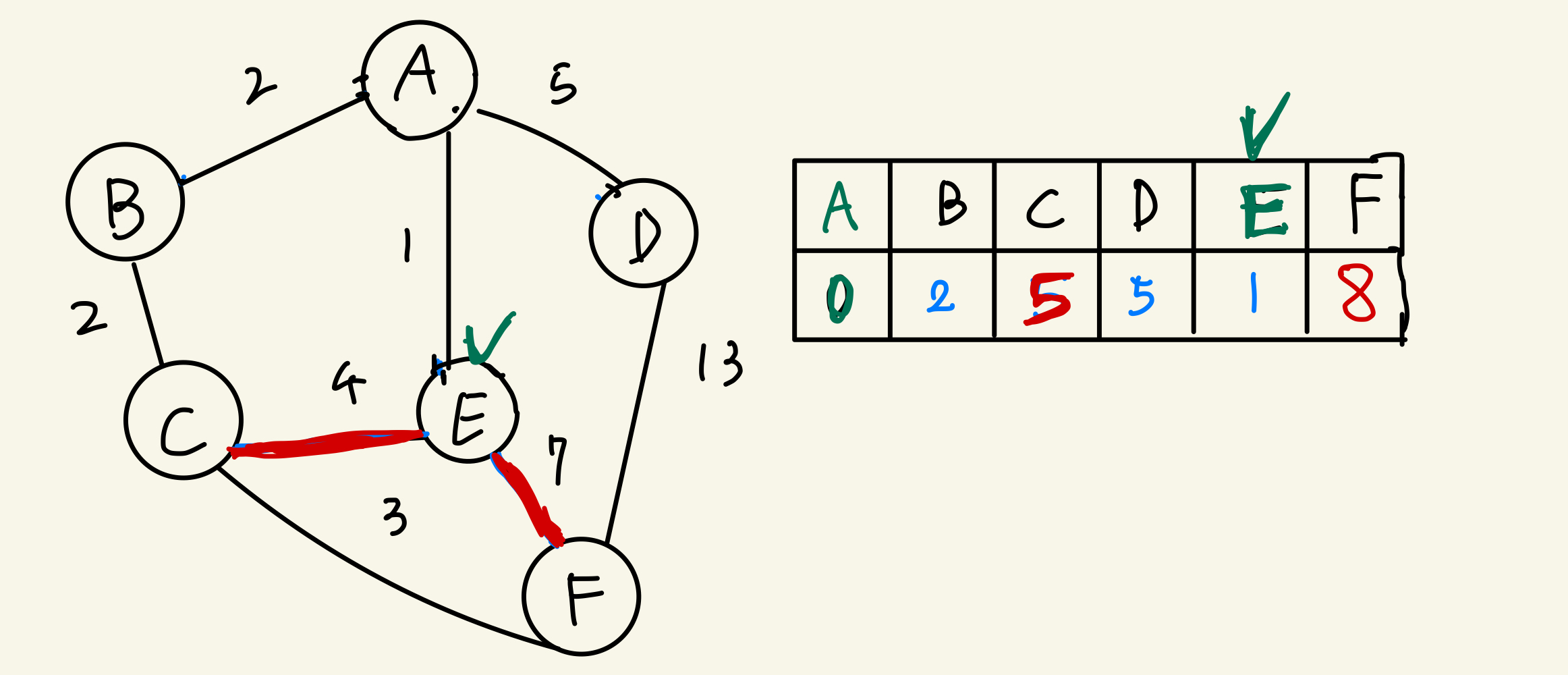
4. 이제 현재정점(E)을 방문처리한 후 다음으로 최단거리인 정점(B)을 선택한후에 똑같은 방식으로 진행을 한다.

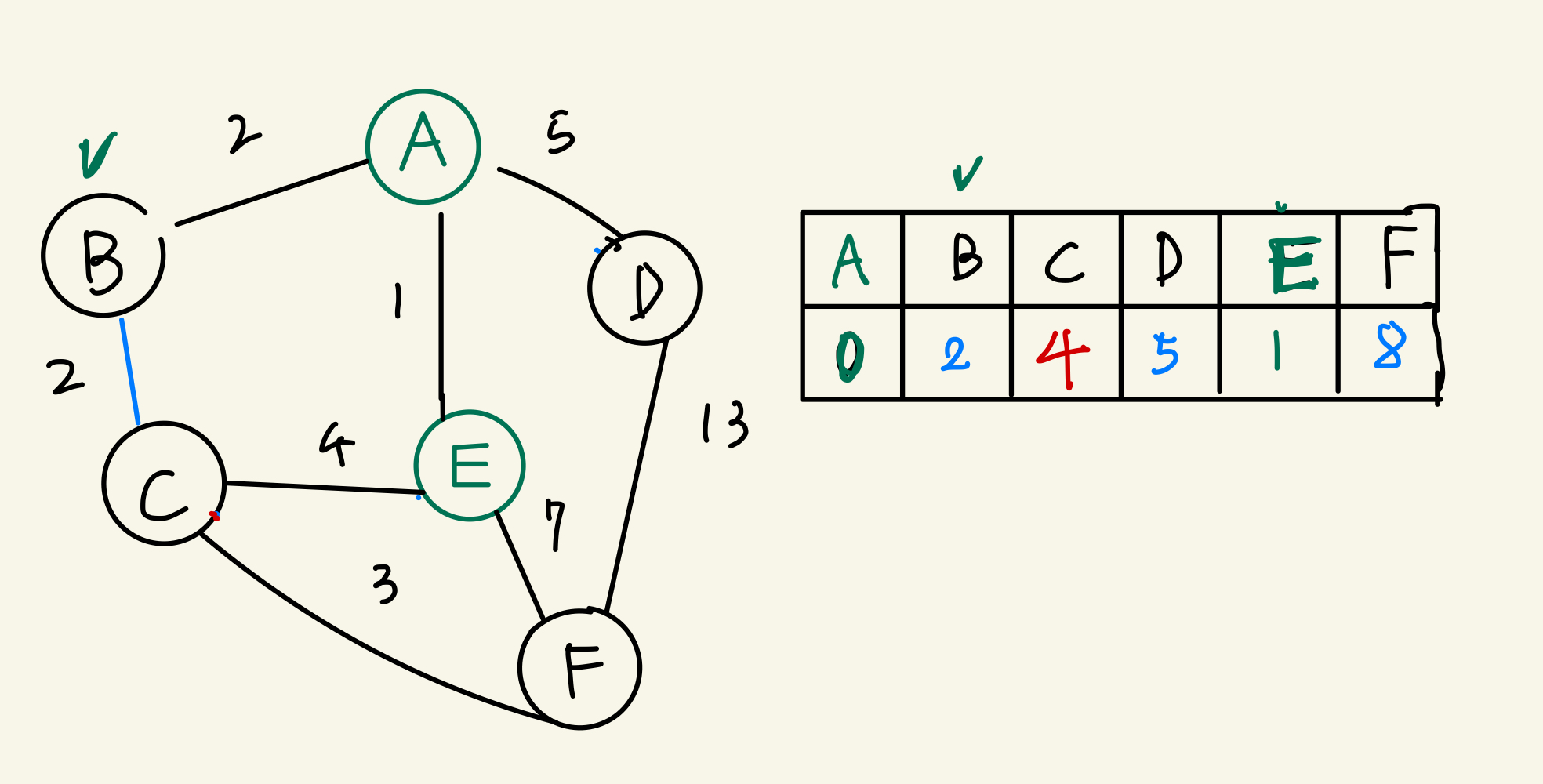
B정점에서 갈수 있는 정점은 C 바께 없음을 확인하실 수 있습니다. 여기서 기존에 C정점의 값이 5였는데 A→B→C 로 가는값이 4다. 즉 기존에 5보다 짧기때문에 다시 C정점에 값을 재할당 해 준다.

5. 계속 이런 절차를 통해서 진행해서 모든 정점이 다 방문처리되면

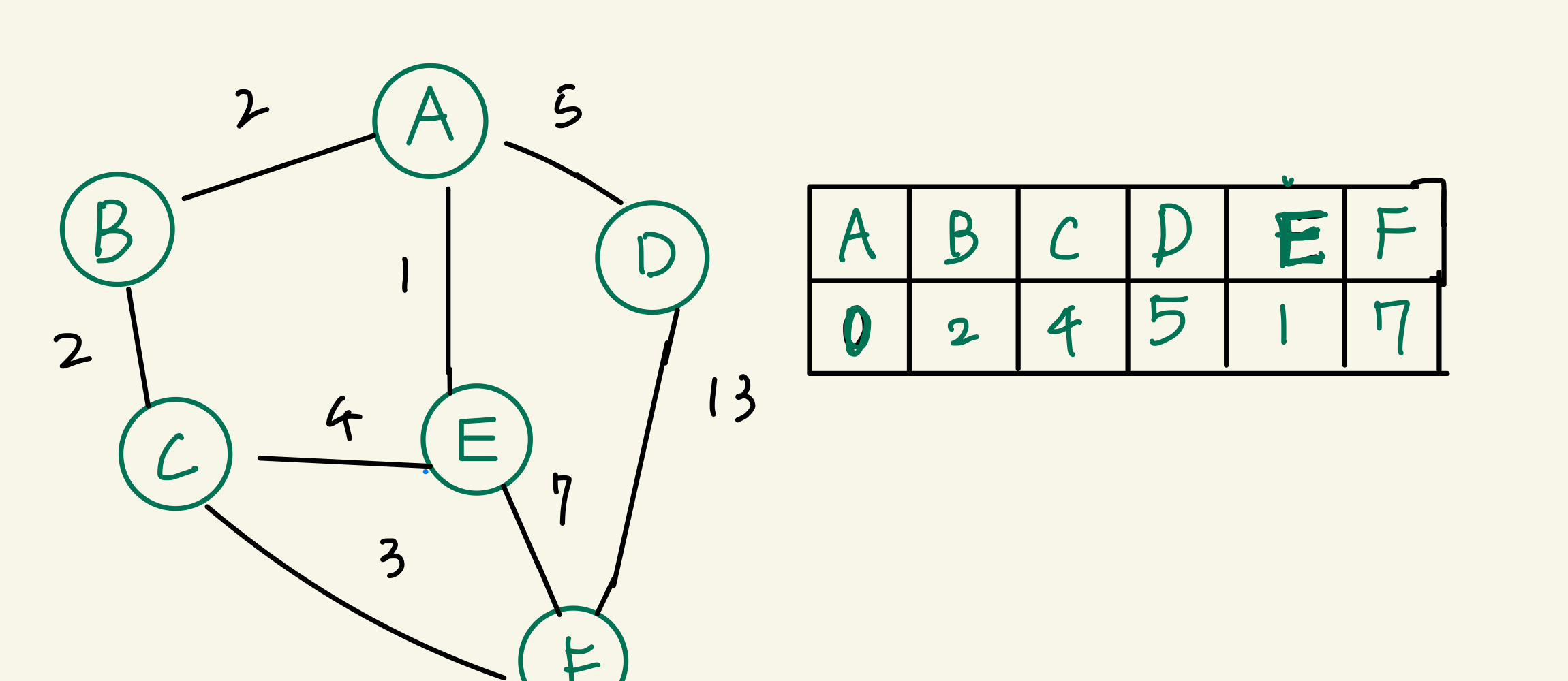
이런식으로 모드 값이 할당된게 보인다.

다익스트라 알고리즘을 보면 계속해서 가장 값이 낮은 정점을 선택하여 진행이되는 것 을 볼 수 있습니다. 따라서 해당 절차를 구현하기 위해서는 우선순위 큐 통해서 구현을 해야합니다. 이를 효율적으로 구현하기 위해서는 힙을 사용하실 수 있습니다.

다익스트라 정리

1. 시작점을 제외한 모든 정점의 거리를 무한으로 설정한다. 시작점은 0으로 설정한뒤 시작한다.
2. 선택한 정점에서 갈 수 있는 정점의 거리를 정점(해당 정점까지의 최단 거리)값 + 간선(거리)값 으로 갱신한다.
3. 선택한 정점을 방문 처리한다.
4. 이미 방문한 정점과 무한인 정점을 제외하고 가장 최단 거리인 정점을 선택한다.
5. 더 이상 방문할 수 있는 정점이 없을 때 까지3~5를 반복.
6. 바지막에 도착의 값을 확인한다.

예제

프로그래머스 배달문제

// 최소힙 
class MinHeap {
  constructor() {
    this.heap = [null];
  }
  push(value) {
    this.heap.push(value);
    let currentIndex = this.heap.length - 1;
    let parentIndex = Math.floor(currentIndex / 2);
    while (
      parentIndex !== 0 &&
      this.heap[parentIndex].cost > this.heap[currentIndex].cost
    ) {
      this._swap(parentIndex, currentIndex);
      currentIndex = parentIndex;
      parentIndex = Math.floor(currentIndex / 2);
    }
  }

  pop() {
    if (this.isEmpty()) return;
    if (this.heap.length === 2) return this.heap.pop();
    const returnValue = this.heap[1];
    this.heap[1] = this.heap.pop();

    let currentIndex = 1;
    let leftIndex = 2;
    let rightIndex = 3;

    while (
      (this.heap[leftIndex] &&
        this.heap[currentIndex].cost > this.heap[leftIndex].cost) ||
      (this.heap[rightIndex] &&
        this.heap[currentIndex].cost > this.heap[rightIndex].cost)
    ) {
      if (this.heap[leftIndex] === undefined) {
        this._swap(currentIndex, rightIndex);
      } else if (this.heap[rightIndex] === undefined) {
        this._swap(currentIndex, leftIndex);
      } else if (this.heap[leftIndex].cost < this.heap[rightIndex]) {
        this._swap(currentIndex, leftIndex);
      } else {
        this._swap(currentIndex, rightIndex);
      }
      leftIndex = currentIndex * 2;
      rightIndex = currentIndex * 2 + 1;
    }
    return returnValue;
  }

  isEmpty() {
    return this.heap.length === 1;
  }

  _swap(a, b) {
    [this.heap[a], this.heap[b]] = [this.heap[b], this.heap[a]];
  }
}

// 다익스트라 알고리즘
function dijkstra(road, N) {
  const heap = new MinHeap();
  heap.push({ node: 1, cost: 0 });

  const dist = [...Array(N + 1)].map(() => Infinity);
  dist[1] = 0;

  while (!heap.isEmpty()) {
    const { node: current, cost: currentCost } = heap.pop();

    for (const [src, dest, cost] of road) {
      const nextCost = cost + currentCost;

      //양방향 고려하여 작성
      if (src === current && nextCost < dist[dest]) {
        // src가 현재 선택된 정점이면서 목적지까지 더 저렴할 경우
        dist[dest] = nextCost; // 거리를 갱신한다.
        heap.push({ node: dest, cost: nextCost });
      } else if (dest === current && nextCost < dist[src]) {
        dist[src] = nextCost;
        heap.push({ node: src, cost: nextCost });
      }
    }

    return dist;
  }
}

function solution(N, road, K) {
  const dist = dijkstra(road, N);
  return dist.filter((x) => x <= K).length;
}