벽 부수고 이동하기

링크: https://www.acmicpc.net/problem/2206
분류: BFS, 그래프 탐색, 너비 우선 탐색
레벨: Gold 3

문제

N×M의 행렬로 표현되는 맵이 있다. 맵에서 0은 이동할 수 있는 곳을 나타내고, 1은 이동할 수 없는 벽이 있는 곳을 나타낸다. 당신은 (1, 1)에서 (N, M)의 위치까지 이동하려 하는데, 이때 최단 경로로 이동하려 한다. 최단경로는 맵에서 가장 적은 개수의 칸을 지나는 경로를 말하는데, 이때 시작하는 칸과 끝나는 칸도 포함해서 센다.

만약에 이동하는 도중에 한 개의 벽을 부수고 이동하는 것이 좀 더 경로가 짧아진다면, 벽을 한 개 까지 부수고 이동하여도 된다.

한 칸에서 이동할 수 있는 칸은 상하좌우로 인접한 칸이다.

맵이 주어졌을 때, 최단 경로를 구해 내는 프로그램을 작성하시오.

입력

첫째 줄에 N(1 ≤ N ≤ 1,000), M(1 ≤ M ≤ 1,000)이 주어진다. 다음 N개의 줄에 M개의 숫자로 맵이 주어진다. (1, 1)과 (N, M)은 항상 0이라고 가정하자.

출력

첫째 줄에 최단 거리를 출력한다. 불가능할 때는 -1을 출력한다.

예제 입력

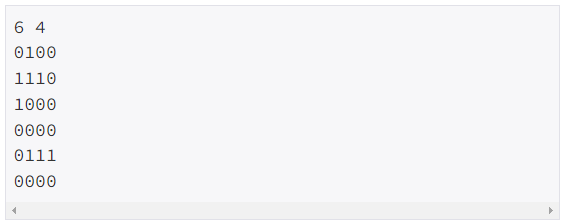
예제 출력

회고

문제 풀이하다 머리가 터져버려서 회고 및 풀이는 짧게 한다....
bfs랑 비슷한 것 같은데, 도저히 구현 방법이 안 떠올라서 힌트글을 참고했다 ㅜ

풀이

벽은 한 번만 깰 수 있기 때문에, 2층짜리 3차원 그래프로 구현한다.
z 값이 0일 경우(1층) 아직 벽을 깨지 않은 경로이고, z 값이 1일 경우(2층) 벽을 깬 경로이다.
그리고 이 문제에서는 벽이 1으므로, 헷갈릴 수 있기 때문에 움직일 때마다 1씩 더해주지 않고 2씩 더해줬다.
마지막에 답을 구할 땐 2로 다시 나눠주고 1을 더하면 된다.

import sys
from collections import deque

input = sys.stdin.readline
N, M = map(int, input().split())
arr = [[],[]]
for i in range(N):
    cur = input().rstrip()
    arr[0].append(list(map(int, cur)))
    arr[1].append(list(map(int, cur)))
q = deque()

def bfs():
    dx = [1, 0, -1, 0]
    dy = [0, 1, 0, -1]
    
    while q:
        x, y, z = q.popleft()
        for i in range(4):
            nx = x + dx[i]
            ny = y + dy[i]
            if 0 <= nx < N and 0 <= ny < M:
                if arr[z][nx][ny] == 0 and z == 0:
                    arr[z][nx][ny] = arr[z][x][y] + 2
                    q.append([nx, ny, 0])
                elif arr[z][nx][ny] == 0 and z == 1:
                    arr[z][nx][ny] = arr[z][x][y] + 2
                    q.append([nx, ny, 1])
                elif arr[z][nx][ny] == 1 and z == 0:
                    arr[1][nx][ny] = arr[0][x][y] + 2
                    q.append([nx, ny, 1])
    
    return

q.append([0, 0, 0])
bfs()

A = arr[0][N-1][M-1]
B = arr[1][N-1][M-1]

if N == M == 1:
    print(1)
elif min(A, B) == 0:
    if A == B:
        print(-1)
    else:
        print(int(max(A, B)/2 + 1))
else:
    print(int(min(A, B)/2 + 1))

참고로 기가 막힌 반례가 있었는데,
N, M이 둘 다 1인 1x1 행렬일 경우 정답은 1인데 계속 0을 출력해서 오답이었다.
심지어 어려운 반례도 아니어서 찾느라 한참 걸린,,,,
항상 기본 조건을 잘 기억하자 ㅠㅠ