[SSAFY][D2]swea_2001 파리퇴치

피용희·2024년 5월 3일

문제

풀이

첫 풀이(greedy)

쉽게 풀자면 쉽게 풀 수 있는 문제고, 규칙을 찾자면 또 규칙을 찾을 수 있는 문제이다.
우선 처음 접근했던 방식은, 무식하게 쭉 돌면서 수를 더해서 max 값을 갱신하는 방식이었다. 정리하면 다음과 같다.

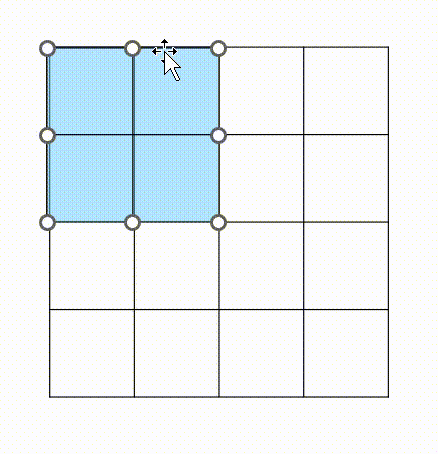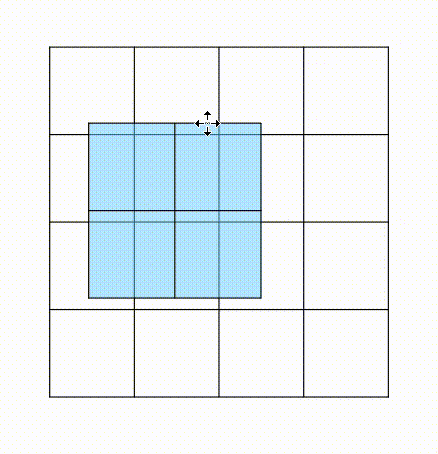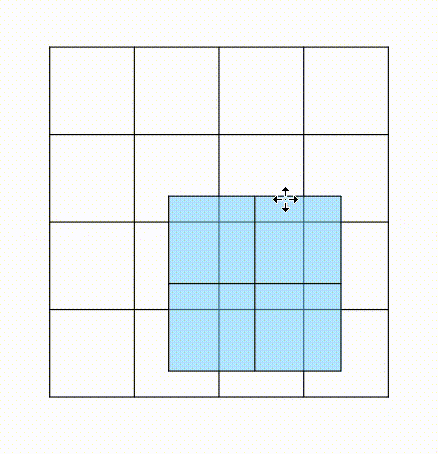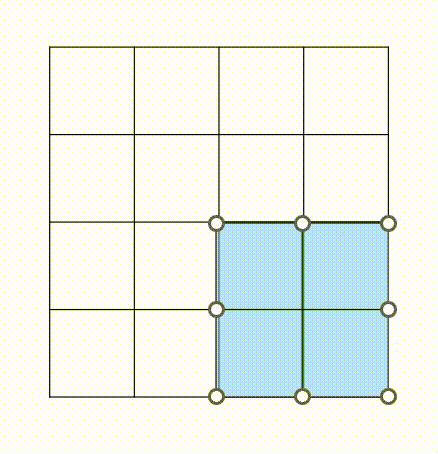
m*m 배열을 n만큼 움직인다. 처음에는 j(열)만 옮기고, 끝 부분이 n과 같아지면 열은 초기화, 행을 +1칸씩 옮긴다.

이 과정은 행이 n보다 커지면 끝난다.

import java.util.Scanner;

/*
 * 파리채 문제
 * n m이 주어진다.
 * m을 배열로 두고, n을 계속 움직이면서 계산하는게 좋을 것 같음
 * greedy 문제..?
 */

public class swea_2001 {
	public static void main(String[] args) {
		Scanner sc  = new Scanner(System.in);
		int num = sc.nextInt();
		StringBuilder stb = new StringBuilder();
		
		for(int z = 1; z<=num; z++) {
			
			int n = sc.nextInt();
			int m = sc.nextInt();
			
			int iEnd = m;
			int iStart = 0;
			
			int jEnd = m;
			int jStart = 0;
			int ans = 0;
			
			int[][] fly = new int[n][n];
			
			for(int i = 0; i<n; i++) {
				for(int j = 0; j<n; j++) {
					fly[i][j] = sc.nextInt();
				}
			}
			
			while(iEnd <= n) {
				while(jEnd <= n) {
					int max = 0;
					for(int i = iStart; i< iEnd; i++) {
						for(int j = jStart; j< jEnd; j++) {
							max += fly[i][j];
						}
					}
					if(max > ans) {
						ans = max;
					}
					jStart++;
					jEnd++;
				}
				iStart++;
				iEnd++;
				
				jStart = 0; //초기화
				jEnd = m;
			}
			
			stb.append("#" + z + " " + ans);
			stb.append("\n");
		}
		System.out.println(stb);
	}

}

최적화 풀이

시간이나 메모리 자체가 넉넉하게 주어진 만큼(d2문제라 그런듯..)이렇게 풀어도 상관 없긴 하지만, 원리를 자세하게 보면, 결국 j(열)이 이동하는 부분이 반복된다는 것을 알 수 있다. 또한, 움직일때 겹치는 부분이 존재한다. 즉, "DP"로 좀더 빠르게 푸는 것도 가능하다!

4X4 배열을 2x2의 파리채로 이동할때를 예시로 살펴보자.

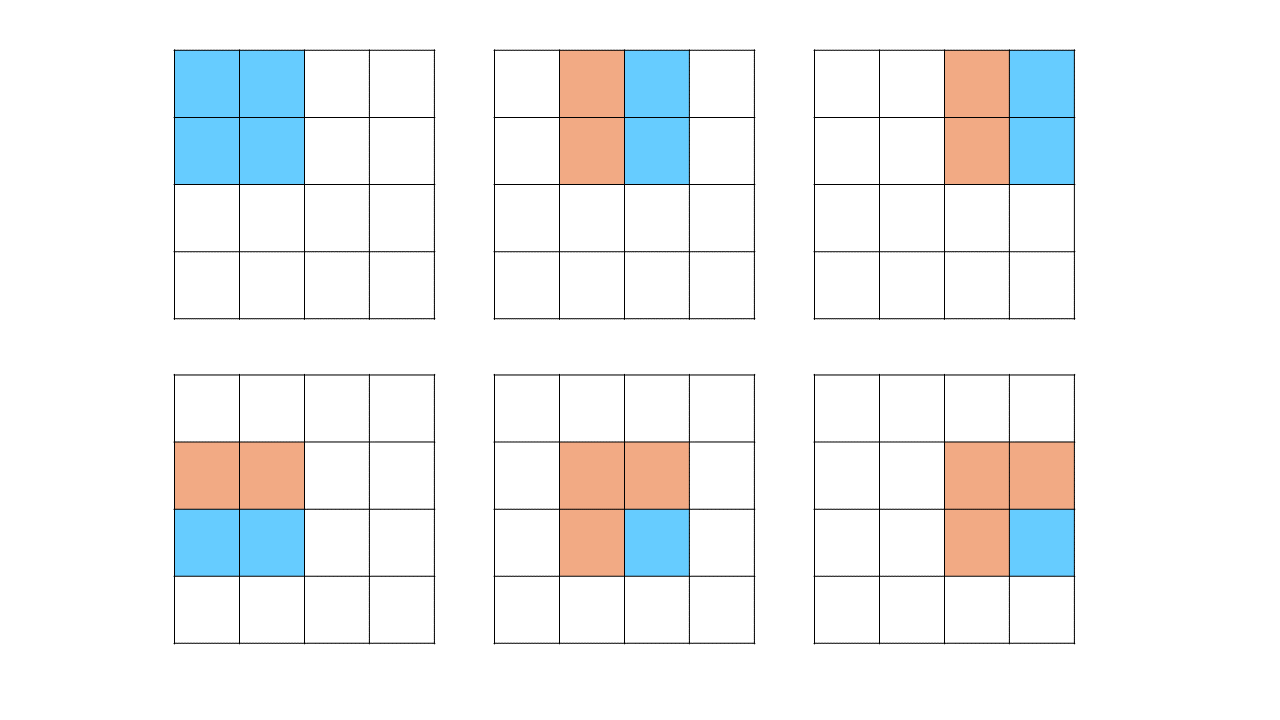
자세히 보면, 주황색으로 이전과 겹치는 부분이 존재한다는 것을 알 수 있다.
즉, 배열을 생성해서 누적합을 저장한다음, 값이 있는 경우 그대로 사용하는 방식을 활용하면 iteration 연산 과정을 줄일 수 있다.

그렇다면 누적합은 어떤식으로 저장하는게 좋을까?

sum(i+1, j+1) = sum(i-1,j) + sum(i,j-1) - sum(i-1,j-1); 로 정의한다.
(식 정의하는 부분은 고민하다가 다른 분의 풀이 레퍼런스를 참고했다...다음에 꼭 다시 한 번 풀어보기)

왜 이런식이 도출될까?

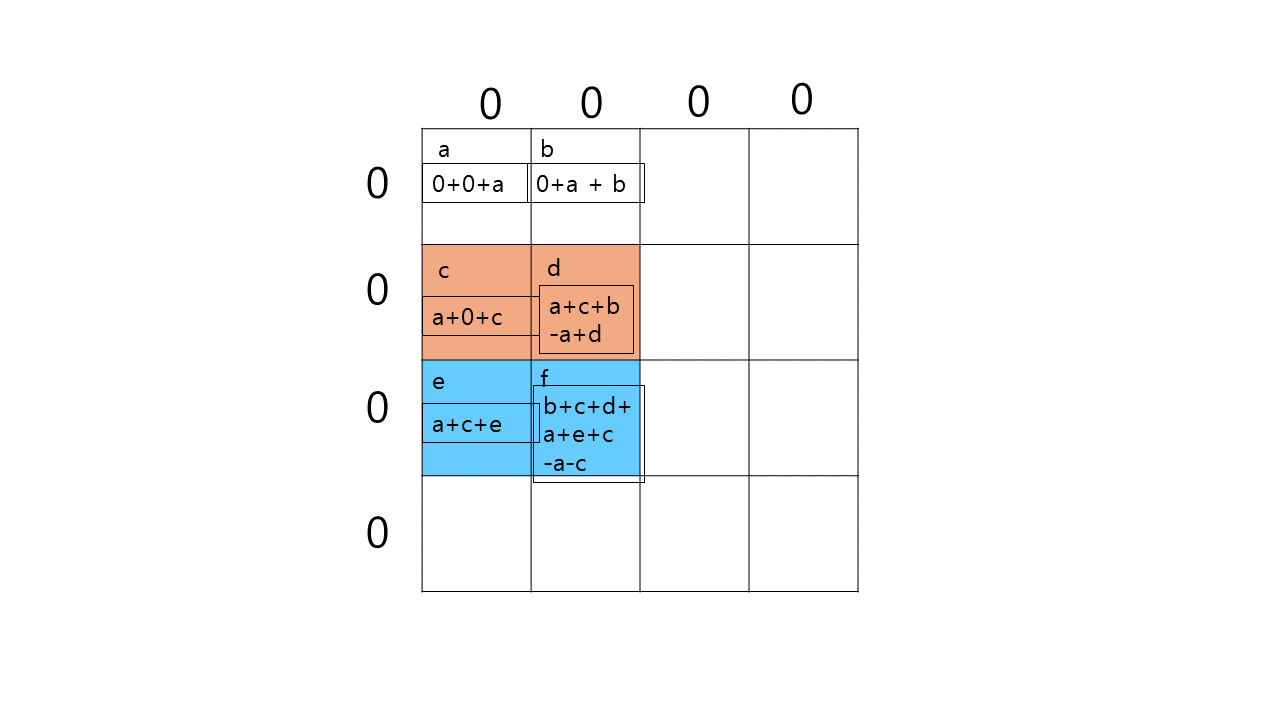
이런식으로 누적값이 해당 칸의 합들로만 이뤄지게 되기 때문이다.(이 부분은 솔직히 이해하는데 좀 시간이 걸렸어서 익숙해지는 과정이 필요할 것 같다.)

그럼, 이 풀이를 바탕으로 새로운 코드를 도출해보자.

public static void main(String[] args) {
		Scanner sc  = new Scanner(System.in);
		int num = sc.nextInt();
		StringBuilder stb = new StringBuilder();
		
		for(int z = 1; z<=num; z++) {
			int n = sc.nextInt();
			int m = sc.nextInt();
			int[][] fly = new int[n+1][n+1];
			int[][] dp = new int[n+1][n+1];
			int max = 0;
			
			for(int i = 0; i<=n; i++) {
				for(int j = 0; j<=n;j++) {
					
					if(i==0 || j == 0) {
						fly[i][j] = 0;
						continue;
					}
					
					fly[i][j] = sc.nextInt();
					
				}
			}
			
			for(int i = 1; i<=n; i++) {
				for(int j = 1; j<=n;j++) {
					dp[i][j] = fly[i][j] + dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1];
				}
			}
			
			int icheck = m;
			int jcheck = m;
			
			for(int i = 0; i<=n-m; i++) {
				//m씩 뛰어넘기
				for(int j = 0; j<=n-m;j++) {
					int dpp = dp[i][j] - dp[icheck][j] - dp[i][jcheck] + dp[icheck][jcheck];
					if(dpp > max) {
						max = dpp;
					}
					jcheck++;
				}
				icheck++;
				jcheck = m; //초기화
			}
			
			stb.append("#");
			stb.append(z+" ");
			stb.append(max);
			stb.append("\n");
		}
		System.out.println(stb);
	}

** 사실 누적합 구하는건 그렇다 치고, 마지막에 m단위로 쪼갤 때 m뒤의 누적값들을 잘라내야 한다는 생각을 하는 것이 상당히 어려웠다ㅠ 더 깔끔하게 잘 작성하신 분들 코드로 나중에 정리 한 번 더 해야지...