
종만북) 28장 그래프의 깊이 우선 탐색
이 포스팅은 <프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략>, 구종만, 인사이트(2012)을 읽고 개인 학습용으로 정리한 글입니다.
➖ 21-09-20
오일러 서킷
-
오일러 서킷(Eulerian Circuit):
그래프의 모든 간선을 정확히 한 번씩 지나서 시작점으로 돌아오는 경로 (= 한붓 그리기) -
무방향 그래프에서 오일러 서킷이 존재하는 필요 충분 조건:
- 그래프의 모든 간선이 하나의 컴포넌트에 포함되어 있다
- 그래프의 모든 정점이 짝수점이다
오일러 서킷을 찾아내는 알고리즘
-
어떤 그래프의 모든 정점이 짝수점이고, 모든 간선이 하나의 컴포넌트에 포함되어 있다
-
findRandomCircuit(u):
임의의 정점 u에서 시작해 아직 따라가지 않은 간선 중 하나를 따라가며 임의의 경로를 만드는 함수
-> 현재 정점에 인접한 간선 중 아직 따라간 적 없는 임의의 간선을 따라가기를 반복하다가, 더이상 따라갈 간선이 없을 때 종료
-> 그래프의 모든 정점은 짝수점이므로, 항상 시작점에서 끝나게 되어 찾아낸 경로는 서킷이 된다 -
findRandomCircuit()로 찾은 서킷이 모든 간선을 지나쳤다면, 오일러 서킷이다
-
findRandomCircuit()로 찾은 서킷이 모든 간선을 지나치지 않았다면, 서킷의 각 정점들을 다시 돌아보며, 아직 따라가지 않은 간선과 인접해있는 정점 v를 찾는다
-> v에서 시작하도록 findRandomCircuit()를 다시 수행한다
-> 처음에 찾았던 서킷을 v에서 자른 뒤, 새로운 서킷을 끼워넣어 하나의 큰 서킷을 만들 수 있다
-> 이와 같은 일을 모든 간선을 다 포함할 때까지 반복하면 오일러 서킷을 찾을 수 있다

⚡깊이 우선 탐색을 이용한 구현
- findRandomCircuit()를 깊이 우선 탐색처럼 재귀 호출로 구현
//깊이 우선 탐색을 이용한 오일러 서킷 찾기
//그래프의 인접 행렬 표현
//adj[i][j]: i와 j사이의 간선의 수
vector<vector<int>> adj;
void getEulerCircuit(int here, vector<int>& circuit){
//adj.size() = 그래프의 정점의 수 = |V|
for(int there = 0; there < adj.size(); ++there){
while(adj[here][there] > 0){
adj[here][there]--;
adj[there][here]--;
getEulerCircuit(there, circuit);
}
}
circuit.push_back(here);
}오일러 트레일
-
오일러 트레일(Eulerian trail):
오일러 서킷처럼 그래프의 모든 간선을 정확히 한 번씩 지나지만, 시작점과 끝점이 다른 경로 -
점 a에서 시작하여 b로 끝나는 오일러 트레일
-> a와 b사이에 간선 (b, a)를 추가한 뒤 오일러 서킷을 찾는다
-> 간선 (b, a)를 지워서 서킷을 끊는다 -
무방향 그래프에서 오일러 트레일이 존재하는 필요 충분 조건:
- 그래프의 모든 간선이 하나의 컴포넌트에 포함되어 있다
- 그래프의 두 정점(시작점 & 끝점)은 홀수점이고, 나머지 모든 정점이 짝수점이다
➖
단어 제한 끝말잇기 (WORDCHAIN)
-
단어 제한 끝말잇기는 일반적인 끝말잇기와 달리 사용할 수 있는 단어의 종류가 미리 정해져 있으며, 한 단어를 두 번 사용할 수 없다
-
단어 제한 끝말잇기에서 사용할 수 있는 단어들의 목록이 주어질 때, 단어들을 전부 사용하고 게임이 끝날 수 있는 지, 그럴 수 있다면 어떤 순서로 사용해야 하는지 계산하라
해밀토니안 경로와 오일러 트레일

-
문제를 방향 그래프로 표현하는 가장 직관적인 방법:
그래프의 정점: 입력으로 주어진 각 단어
그래프의 간선: 한 단어의 마지막 글자가 다른 단어의 첫 글자와 같다면 간선 추가 -
이 방향 그래프로 단어 제한 끝말잇기의 순서를 구하는 방법:
그래프의 모든 정점을 정확히 한 번씩 지나는 경로 찾기
= 해밀토니안 경로(Hamiltonian path) 찾기 -
⚡해밀토니안 경로를 찾는 유일한 방법: 조합 탐색
-> 모든 정점의 배열을 하나하나 시도하며 이들이 경로가 되는지를 확인해야 한다
-> 최악의 경우 n!개의 후보를 만들어야 한다

-
문제를 방향 그래프로 표현하는 다른 방법:
그래프의 정점: 알파벳의 각 글자 (입력으로 주어진 각 단어의 첫 글자 & 마지막 글자)
그래프의 간선: 입력으로 주어진 각 단어 -
이 방향 그래프로 단어 제한 끝말잇기의 순서를 구하는 방법:
그래프의 모든 간선을을 정확히 한 번씩 지나는 경로 찾기
= 오일러 서킷/트레일 찾기 -
끝말잇기 문제의 입력을 그래프로 만들기
//그래프의 인접 행렬 표현
//adj[i][j]: i와 j사이의 간선의 수
vector<vector<int>> adj;
//graph[i][j]: i로 시작해서 j로 끝나는 단어의 목록(= 간선의 목록)
vector<string> graph[26][26];
//indegree[i]: i로 시작하는 단어의 수(= i로 들어가는 간선의 수)
//outdegree[i]: i로 끝나는 단어의 수(= i로부터 나오는 간선의 수)
vector<int> indegree, outdegree;
void makeGraph(const vector<string>& words){
//전역 변수 초기화
for(int i = 0; i<26; ++i){
for(int j = 0; j<26; ++j){
graph[i][j].clear();
}
}
adj = vector<vector<int>> (26, vector<int>(26, 0));
indegree = outdegree = vector<int> (26, 0);
//각 단어 그래프에 추가
for(int i = 0; i<words.size(); ++i){
//단어의 첫 글자 a, 마지막 글자 b
int a = words[i][0] - 'a';
int b = words[i][words[i].size()-1] - 'a';
graph[a][b].push_back(words[i]);
adj[a][b]++;
outdegree[a]++;
indegree[b]++;
}
}방향 그래프에서 오일러 서킷/트레일
- 방향 그래프에서 오일러 서킷이 존재하는 필요 충분 조건:
- 간선들의 방향을 무시했을 때 방향 그래프의 정점들이 서로 연결되어 있어야 한다
- 각 정점에 들어오는 간선의 수와 나가는 간선의 수가 같아야 한다
- 방향 그래프에서 오일러 트레일이 존재하는 필요 충분 조건:
- 간선들의 방향을 무시했을 때 방향 그래프의 정점들이 서로 연결되어 있어야 한다
- 한 정점은 나가는 간선이 들어오는 간선보다 하나 많고(시작점),
한 정점은 들어오는 간선이 나가는 간선보다 하나 많고(끝점),
나머지 모든 각 정점에 들어오는 간선의 수와 나가는 간선의 수가 같아야 한다
⚡오일러 서킷/트레일을 찾아내는 알고리즘의 구현
-
그래프에 오일러 서킷 혹은 트레일이 존재한다고 가정
-
각 정점의 차수를 확인하여, 나가는 간선의 수가 들어오는 간선의 수보다 하나 많은 정점이 있는지 확인
-> 있다면 이 정점을 시작점으로 하여 오일러 트레일을 찾는다
-> 없다면 아무 정점을 시작점으로 하여 오일러 서킷을 찾는다
//방향 그래프에서 오일러 서킷 혹은 트레일 찾아내기
//방향 그래프의 인접 행렬 adj가 주어졌을 때 오일러 서킷 혹은 트레일 계산
void getEulerCircuit(int here, vector<int>& circuit){
for(int there = 0; there < adj.size(); ++there){
while(adj[here][there] > 0){
adj[here][there]--;
getEulerCircuit(there, circuit);
}
}
circuit.push_back(here);
}
//현재 그래프의 오일러 트레일이나 서킷 반환
vector<int> getEulerTrailOrCircuit(){
vector<int> circuit;
//나가는 간선의 수가 들어오는 간선의 수보다 하나 많은 정점이 있는지 확인
for(int i = 0; i< adj.size(); ++i){
if(outdegree[i] == indegree[i] + 1){
//이 정점을 시작점으로 하여 오일러 트레일을 찾는다
getEulerCircuit(i, circuit);
return circuit;
}
}
//아무 정점을 시작점으로 하여 오일러 서킷을 찾는다
for(int i = 0; i< adj.size(); ++i){
if(outdegree[i]){
getEulerCircuit(i, circuit);
return circuit;
}
}
//모두 실패한 경우 빈 배열을 반환한다
return circuit;
}오일러 서킷/트레일의 존재 여부 확인
//끝말잇기 문제의 오일러 서킷/트레일 존재 여부 확인
bool checkEuler(){
//예비 시작점: 나가는 간선이 들어오는 간선보다 하나 큰 점
//예비 끝점: 나가는 간선이 들어오는 간선보다 하나 작은 점
//예비 시작점과 예비 끝점의 개수
int plus1 = 0, minus1 = 0;
for(int i = 0; i<26; ++i){
int delta = outdegree[i] - indegree[i];
if(delta < -1 || delta > 1) return false;
if(delta == 1) plus1++;
if(delta == -1) minus1++;
}
return ((plus1 == 1 && minus1 == 1) || (plus1 == 0 && minus1 == 0));
}단어 제한 끝말잇기 문제 풀이
string solve(const vector<string>& words){
//끝말잇기 문제의 입력을 그래프로 만들기
makeGraph(words);
//끝말잇기 문제의 오일러 서킷/트레일 존재 여부 확인
if(!checkEuler()) return "IMPOSSIBLE";
//오일러 서킷/트레일 찾기
vector<int> circuit = getEulerTrailOrCircuit();
//오일러 서킷/트레일이 되기 위해선 모든 간선이 하나의 컴포넌트에 포함되어야
//모든 간선을 방문하지 못한 경우 실패
if(circuit.size()-1 != words.size()) return "IMPOSSIBLE";
//방문 순서를 뒤집은 뒤 간선들을 모아 문자열로 만들어 반환
reverse(circuit.begin(), circuit.end());
string ret;
for(int i = 1; i<circuit.size(); ++i){
int a = circuit[i-1], b = circuit[i];
//반환된 문자열에서 첫 단어가 아닌 경우 " " 추가
if(ret.size()) ret += " ";
ret += graph[a][b].back();
graph[a][b].pop_back();
}
return ret;
}
➖ 21-09-25
위상 정렬
-
의존성이 있는 작업들이 주어질 때, 이를 의존성 그래프로 표현할 수 있다
-
의존성 그래프(dependency graph)
정점: 각 작업
간선: 각 작업 간의 의존 관계
-> 작업 v가 작업 u에 의존할 때(= 작업 v를 하기 전 반드시 작업 u를 해야할 때) 의존성 그래프는 간선 (u, v)를 포함한다 -
의존성 그래프의 특성: 그래프에 사이클이 없다
-> 사이클 없는 방향 그래프 (directed acyclic graph, DAG)이다 -
위상 정렬(topology sort):
의존성이 있는 작업들이 주어질 때, 이들을 어떤 순서로 수행해야 하는지 계산
= 의존성 그래프에서 모든 의존성이 만족되도록 정점의 순서를 배열
= DAG에서 모든 간선이 동일한 방향으로 가도록 정점을 배열
- 위상 정렬의 가장 직관적인 구현 방법:
들어오는 간선이 하나도 없는 정점들을 하나씩 찾아서 정렬 결과 뒤에 붙이고,
그래프에서 이 정점을 지우는 과정을 반복한다
-> 적절한 자료 구조 사용하여 구현 가능
(큐를 사용한 구현: https://velog.io/@sunjoo9912/TIL-21-07-08)
-> 깊이 우선 탐색 이용하여 구현 가능
⚡깊이 우선 탐색을 이용한 위상 정렬 구현
- dfsAll()을 수행하며 dfs()가 종료될 때마다 현재 정점의 번호를 기록한다
dfsAll()이 종료한 뒤 기록된 순서를 뒤집으면 위상 정렬 결과를 얻을 수 있다
⚡알고리즘의 정당성 증명
- dfs()의 종료 역순으로 정점들을 늘어 놓았을 때, 그림과 같이 오른쪽에서 왼쪽으로 가는 간선(u,v)이 존재할 수 있을까?

-
정점 u가 정점 v의 오른쪽에 있다
= dfs(u)가 종료한 후 dfs(v)가 종료했다
= dfs(u)가 호출되었을 때, dfs(v)는 이미 실행 중이었다
= dfs(v)에서 재귀 호출을 거쳐 dfs(u)가 호출되었다
= 그래프에 v에서 u로 가는 경로가 존재한다 -
간선 (u, v)가 있다고 가정하면, 사이클이 되므로 DAG라는 의존 그래프의 특성에 모순된다
-> 오른쪽에서 왼쪽으로 가는 간선이 존재할 수 없다
-> 따라서 dfs()의 종료 역순으로 정점들을 늘어 놓으면 적절한 위상 정렬이 된다
➖
고대어 사전(DICTIONARY)
-
사전에 포함된 단어들의 목록이 순서대로 주어질 때 이 언어에서 알파벳 숫서를 계산하기
-
알파벳들의 순서에 모순이 있다면 "INVALID HYPOTHESIS"를 출력한다
모순이 없다면 26개의 소문자로 알파벳들의 순서 출력한다 (가능한 순서가 여러 개라면 아무 것이나 출력)
그래프 모델링
-
단어 A가 B보다 사전에 먼저 출현하는 경우
-> 두 단어를 첫 글자부터 비교하면서, 처음으로 다른 글자를 찾는다
-> A의 해당 글자는 B의 해당 글자보다 앞에 와야 한다 -
방향 그래프로 표현:
정점: 26개 알파벳 소문자
간선: 한 알파벳이 다른 알파벳 앞에 와야할 때 두 정점 방향 간선으로 연결
-> 우리가 원하는 알파벳들의 순서는 이 방향 그래프의 위상 정렬 결과가 된다
//고대어 사전 문제의 그래프 생성
//알파벳의 각 글자에 대한 인접 행렬 표현
//adj[i][j]: 글자 i가 글자 j보다 먼저 와야함을 나타낸다
vector<vector<int>> adj;
void makeGraph(const vector<string>& words){
adj = vector<vector<int>>(26, vector<int>(26, 0));
for(int j = 1; j < words.size(); ++j){
int i = j-1;
int len = min(words[i].size(), words[j].size());
for(int k = 0; k < len; ++k){
if(words[i][k] != words[j][k]){
int a = words[i][k] - 'a';
int b = words[j][k] - 'a';
adj[a][b] = 1;
break;
}
}
}
}-
앞에 오는 단어가 뒤에 오는 단어의 접두사일 때, 알 수 있는 정보는 없다
-
사전순으로 인접한 단어들만 검사하더라도 그래프의 위상 정렬 결과는 모든 단어 쌍을 검사했을 때와 같다
위상 정렬의 구현
- 알고리즘 수행 시간: O(nL) (n: 단어의 개수, L: 단어의 길이)
//깊이 우선 탐색을 이용한 위상 정렬
vector<int> seen, order;
//깊이 우선 탐색을 진행하며 dfs종료 순서 기록
void dfs(int here){
seen[here] = 1;
for(int there = 0; there < 26; ++there){
if(adj[here][there] && !seen[there])
dfs(there);
}
order.push_back(here);
}
//adj에 주어진 그래프 위상 정렬한 결과 반환
//그래프가 DAG가 아니라면 빈 벡터 반환
vector<int> topologicalSort(){
int n = adj.size();
seen = vector<int>(n, 0);
order.clear();
//dfsAll
for(int i = 0; i<n; ++i){
if(!seen[i]) dfs(i);
}
//dfs 종료 역순으로 뒤집기
reverse(order.begin(), order.end());
//만약 정렬 결과에 역방향 간선이 있다면 DAG가 아니다
for(int i = 0; i<n; ++i){
for(int j = i + 1; j <n; ++j){
if(adj[order[j]][order[i]]) return vector<int>();
}
}
return order;
}
📌 참고자료
- 위상 정렬(Topological Sort)
https://namnamseo.tistory.com/entry/Topological-Sort-%EC%9C%84%EC%83%81%EC%A0%95%EB%A0%AC
➖ 21-09-26
이론적 배경과 응용
-
깊이 우선 탐색을 수행하면 그 과정에서 그래프의 모든 간선을 한 번씩은 만나게 된다
-> 일부 간선은 처음 발견한 정점으로 연결되어 따라가게 된다
-> 일부 간선은 이미 발견한 정점으로 연결되어 무시하게 된다 -
깊이 우선 탐색에서 간선들을 무시하지 않고 정보를 수집하면, 그래프의 구조에 대해 많은 것을 알 수 있다
깊이 우선 탐색과 간선의 분류
-
그래프를 깊이 우선 탐색했을 때, 탐색이 따라가는 간선들만 모아보면 트리 형태를 띤다
= 그래프의 깊이 우선 탐색 스패닝 트리 = DFS 스패닝 트리(DFS Spanning Tree) -
그래프의 DFS 스패닝 트리를 생성하고 나면 그래프의 간선을 네 가지 중 하나로 분류할 수 있다
- 트리 간선(tree edge): DFS 스패닝 트리에 포함된 간선
- 순방향 간선(forwarding edge): DFS 스패닝 트리에는 포함되지 않았지만, 트리의 parent node -> child node를 연결하는 간선
- 역방향 간선(back edge): DFS 스패닝 트리에는 포함되지 않았지만, 트리의 child node -> parent node를 연결하는 간선
- 교차 간선(cross edge): 위 세 가지 분류를 제외한 나머지 간선들
- 깊이 우선 탐색이 어느 순서대로 정점을 방문하느냐에 따라 서로 다른 DFS 스패닝 트리가 생성된다
-> 그에 따라 각 간선의 구분이 서로 달라질 수 있다
무향 그래프 간선의 분류
-
무향 그래프의 모든 간선은 양방향으로 통행 가능하다
-> 순방향 간선과 역방향 간선의 구분이 없다
-> 교차 간선이 있을 수 없다 -
간선 (u, v)가 교차 간선이 되기 위해서는 v가 먼저 방문된 후, u를 방문하지 않고 종료해야 한다
-> 무방향 그래프에서는 (u, v)를 이용해 v에서 u로 갈 수 있다
-> v가 먼저 방문된 후, u를 방문하지 않고 종료되는 경우는 존재하지 않는다
⚡사이클 존재 여부 확인
- 사이클의 존재 여부는 역방향 간선의 존재 여부와 동치이다

- 사이클이 있는 그래프를 깊이 우선 탐색할 경우, 사이클에 포함된 정점 중 깊이 우선 탐색에서 처음 만나는 정점을 u라고 하자
-> dfs(u)는 u에서 갈 수 있는 정점들을 모두 방문한 뒤 종료된다
-> 따라서 깊이 우선 탐색은 사이클에서 u이전에 있는 정점을 dfs(u)가 종료하기 이전에 방문한다
-> 이 정점에서 u로 가는 간선은 항상 역방향 간선이 된다
⚡간선을 구분하는 방법
-
discovered[i]]: 정점 i가 깊이 우선 탐색에서 몇 번째로 발견되었는지 기록한다
finished[i]: dfs(i)가 종료했으면 1, 아니면 0을 저장한다 -
간선 ((u, v)는
-> v가 u보다 늦게 발견된 경우: 순방향 간선
-> v가 u보다 일찍 발견된 경우: dfs(v)가 종료하지 않았다면 역방향 간선, 종료했다면 교차 간선이다
vector<vector<int>> adj;
vector<int> discovered, finished;
//지금까지 발견한 정점의 수
int counter;
//간선을 구분하는 깊이 우선 탐색의 구현
void dfs2(int here){
discovered[here] = counter++;
for(int i = 0; i < adj[here].size(); ++i){
int there = adj[here][i];
cout << "(" << here << ", "<< there << ") is a";
//아직 방문한 적 없다면 방문한다
if(discovered[there] == -1){
cout <<"tree edge\n";
dfs2(there);
}
else if(discovered[here] < discovered[there]){
cout << "forwarding edge\n";
}
else if(discovered[here] > discovered[there]){
if(finished[there] == 0){
cout << "back edge\n";
}
else {
cout << "cross edge\n";
}
}
}
finished[here] = 1;
}➖
절단점 찾기
- 무향 그래프의 절단점(cut vertex): 이 점과 인접한 간선들을 모두 지웠을 때 해당 컴포넌트가 두 개 이상으로 나뉘어지는 정점
절단점 찾기 알고리즘
- 임의의 정점에서부터 깊이 우선 탐색을 통해 DFS 스패닝 트리를 만들었을 때,
어떤 정점 u가 절단점인지 어떻게 알 수 있을까?

-
무방향 그래프의 DFS 스패닝 트리에는 교차 간선이 존재하지 않는다
-> u와 연결된 정점들은 모두 u의 parent이거나 u의 child이다 -
u가 지워졌을 때 그래프가 쪼개지지 않기 위한 유일한 방법
= u의 parent와 u의 child들이 전부 (역방향) 간선으로 연결되어있어야 한다
= u의 자손들이 전부 u의 parent로 올라갈 수 있어야 한다 -
u가 DFS 스패닝 트리의 루트라서 u의 parent가 존재하지 않는 경우,
u가 지워졌을 때 그래프가 쪼개지지 않기 위한 유일한 방법
= 자손이 없거나 하나밖에 없어야 한다
⚡절단점 찾기 알고리즘 구현
//무방향 그래프에서 절단점을 찾는 알고리즘
//그래프의 인접 리스트 표현
vector<vector<int>> adj;
int counter;
//각 정점의 발견 순서 (-1로 초기화)
vector<int> discovered;
//각 정점이 절단점인지 여부 저장 (false)로 초기화
vector<bool> isCutVertex;
//here을 루트로 하는 서브트리에 있는 절단점들을 찾는다
//반환값: 해당 서브트리에서 (역방향) 간선으로 갈 수 있는 정점 중 가장 일찍 발견된 정점의 발견 시점
//처음 호출할 때는 isRoot = true이다
int findCutVertex(int here, bool isRoot){
discovered[here] = counter++;
int ret = discovered[here];
//here가 스패닝 트리의 루트인 경우 절단점 판정을 위해 자손 서브트리의 개수 저장
int children = 0;
for(int i = 0; i<adj[here].size(); ++i){
int there = adj[here][i];
if(discovered[there] == -1){
++children;
//이 서브트리에서 갈 수 있는 가장 일찍 발견된 정점의 발견 시점
int subtree = findCutVertex(there, false);
//그 노드가 here 아래에 있다면 현재 위치는 절단점이 된다
if(!isRoot && subtree >= discovered[here]){
isCutVertex[here] = true;
}
else ret = min(ret, subtree);
}
else ret = min(ret, discovered[there]);
}
//here가 스패닝 트리의 루트인 경우 절단점 판정
if(isRoot && children >= 2) isCutVertex[here] = true;
return ret;
}
-
무향 그래프에서 절단점을 포함하지 않는 서브 그래프
= 이중 결합 컴포넌트(biconnected component) -
이중 결합 컴포넌트 내에서는 임의의 한 정점을 그래프에서 지우더라도 정점간의 연결 관계가 유지된다
다리 찾기
-
어떤 간선을 삭제했을 때 이 간선을 포함하던 컴포넌트가 두 컴포넌트로 쪼개질 경우 이 간선을 다리(bridge)라고 한다
-
그래프에서 다리를 찾는 문제는 절단점을 찾는 알고리즘을 간단히 변형하여 풀 수 있다
다리 찾기 알고리즘
- 다리는 항상 트리 간선이다
-> 어떤 간선 (u, v)가 순방향 간선이거나 역방향 간선이라면 u와 v를 잇는 또다른 경로가 있다는 뜻이다
-> (u, v)는 다리가 될 수 없다

➖ 21-09-27
강결합 컴포넌트 분리
강결합 컴포넌트(strongly connected components, SCC)
-
이중 결합 컴포넌트와 비슷하지만 방향 그래프에서 정의되는 개념이다
-
방향 그래프 상에서 두 정점 u와 v에 대해 양방향으로 가는 경로가 모두 있을 때 두 정점은 같은 SCC에 속해있다고 말한다
-
방향 그래프에서 각 SCC 사이를 연결하는 간선들을 모으면 SCC들을 정점으로 하는 DAG를 만들 수 있다
-> 이 과정을 그래프 압축(condension)이라고 부른다 -
한 사이클에 포함된 정점들은 항상 같은 SCC에 속해있게 된다
-> 반대로 한 SCC에 속한 두 정점 사이를 잇는 양방향 경로를 합치면 두 정점을 포함하는 사이클이 된다 -
그래프가 두 개 이상의 SCC로 나눠진다면, 한 지점에서 다른 지점으로 갈 수 없는 경우가 있다는 의미이다
-> 두 SCC 사이에는 양방향으로 가는 경로가 존재할 수 없기 때문
⚡강결합 컴포넌트 분리를 위한 타잔 알고리즘
- 타잔(Tarjan) 알고리즘: 한 번의 깊이 우선 탐색으로 각 정점을 SCC별로 분리하는 알고리즘

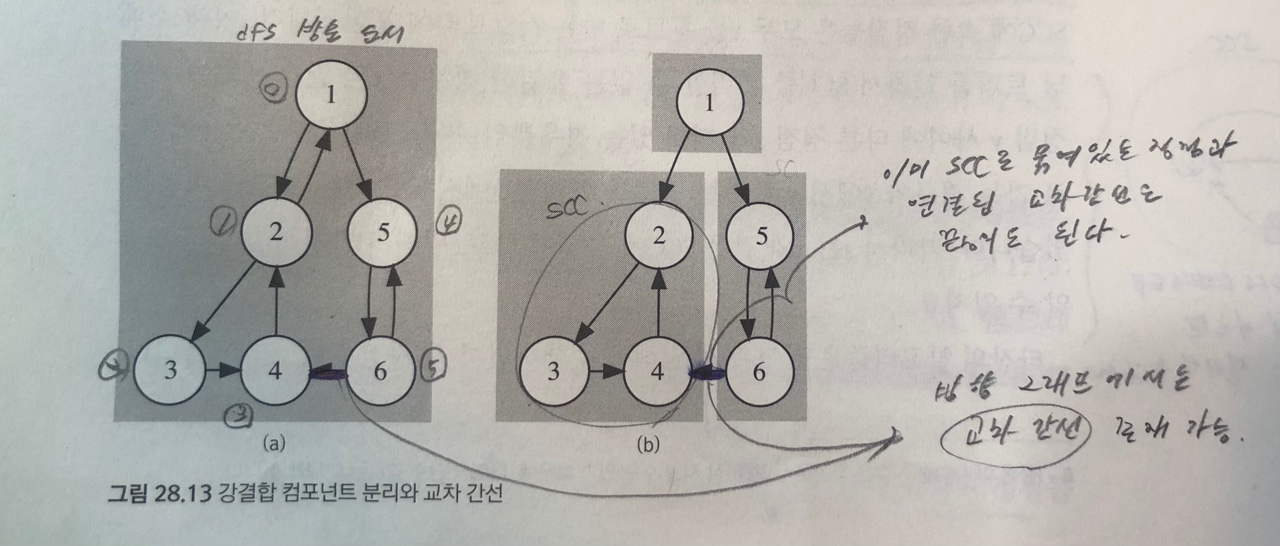
⚡강결합 컴포넌트 분리 알고리즘 구현
//그래프의 인접 리스트 표현
vector<vector<int>> adj;
//각 정점의 컴포넌트 번호 (0부터 시작, 같은 SCC에 속한 정점들은 같은 컴포넌트 번호를 갖는다)
vector<int> sccId;
//각 정점의 발견 순서
vector<int> discovered;
//정점의 번호를 담는 스택
stack<int> st;
int sccCounter, vertexCounter;
//here를 루트로 하는 서브트리에서 역방향 간선이나 교차 간선을 통해 갈 수 있는 정점 중 최소 발견 순서 반환
//이미 SCC로 묶인 정점으로 연결된 간선은 무시한다
int scc(int here){
int ret = discovered[here] = vertexCounter++;
//스택에 here을 넣는다
//here의 자손들은 모두 스택에서 here 위에 쌓이게 된다
st.push(here);
for(int i = 0; i<adj[here].size(); ++i){
int there = adj[here][i];
//(here, there)이 트리 간선인 경우
if(discovered[there] == -1){
ret = min(ret, scc(there));
}
//(here, there)이 무시해야하는 교차 간선이 아닌 경우
else if(sccId[there] == -1){
ret = min(ret, discovered[there]);
}
}
//here에서 부모로 올라가는 간선을 끊어도 되는 경우
//= here를 루트로 하는 서브트리에서 갈 수 있는 정점 중 가장 높은 정점이 here인 경우
if(ret == discovered[here]){
//here을 루트로 하는 서브트리에 남아 있는 정점들을 하나의 컴포넌트로 묶는다
while(true){
int t = st.top();
st.pop();
sccId[t] = sccCounter;
if(t == here) break;
}
sccCounter++;
}
return ret;
}
vector<int> tarjanSCC(){
sccId = discovered = vector<int>(adj.size(), -1);
sccCounter = vertexCounter = 0;
for(int i = 0; i<adj.size(); ++i){
if(discovered[i] == -1)
scc(i);
}
return sccId;
}📌 참고자료
- 강한 결합 요소(Strongly Connected Component)
https://www.youtube.com/watch?v=H_Cg3-rv7RU
