알고리즘 수업 과제1 (생일 문제)

*나는 기본적으로 파이썬을 이용하여 코드를 작성할 것이다.

첫번째 문제: 주어진 생일 데이터(수강자 100명정도의 생일이 작성된 파일)에서 동일한 생일자 쌍의 수를 구하여라.

내가 생각해본 알고리즘:
1. 생일 데이터를 하나씩 리스트 형태로 넣는다.
2. 이때 이진 탐색을 활용하여 동일한 생일날짜가 있는지 검사한다. 있을 경우 -> count + 1 후 삽입, 없을 경우 -> 해당 위치에 삽입.

pseudo code:

DATA = read birth_date
bool search(target):
	while left <= right
	if nums[mid] < target:
    	left = mid + 1
    elif nums[mid] > target:
    	right = mid - 1
    elif nums[mid] == target:
    	count += 1
        
for i in DATA
	

이런 알고리즘을 사용하여 문제를 풀려고 하였으나, 삽입을 하는 방식을 구현하기가 어려워 찾아보니 더 구현이 쉬운 판다스 함수가 있어 이를 활용하기로 하였다.

사용하는 판다스 함수: duplicated -> 중복 여부 확인

import pandas as pd
df = pd.read_csv('/Users/hansunkyoung/Projects/algorithm/BirthdayData.csv', encoding='UTF-8')
birth_df = df.iloc[1:, 2:3]
birth_df.columns = ['Birthday']
print(birth_df.duplicated('Birthday').sum())

두번째 문제: k명의 학생에서 생일이 같은 학생이 두명 이상 있을 확률을 계산하는 코드를 작성하라.

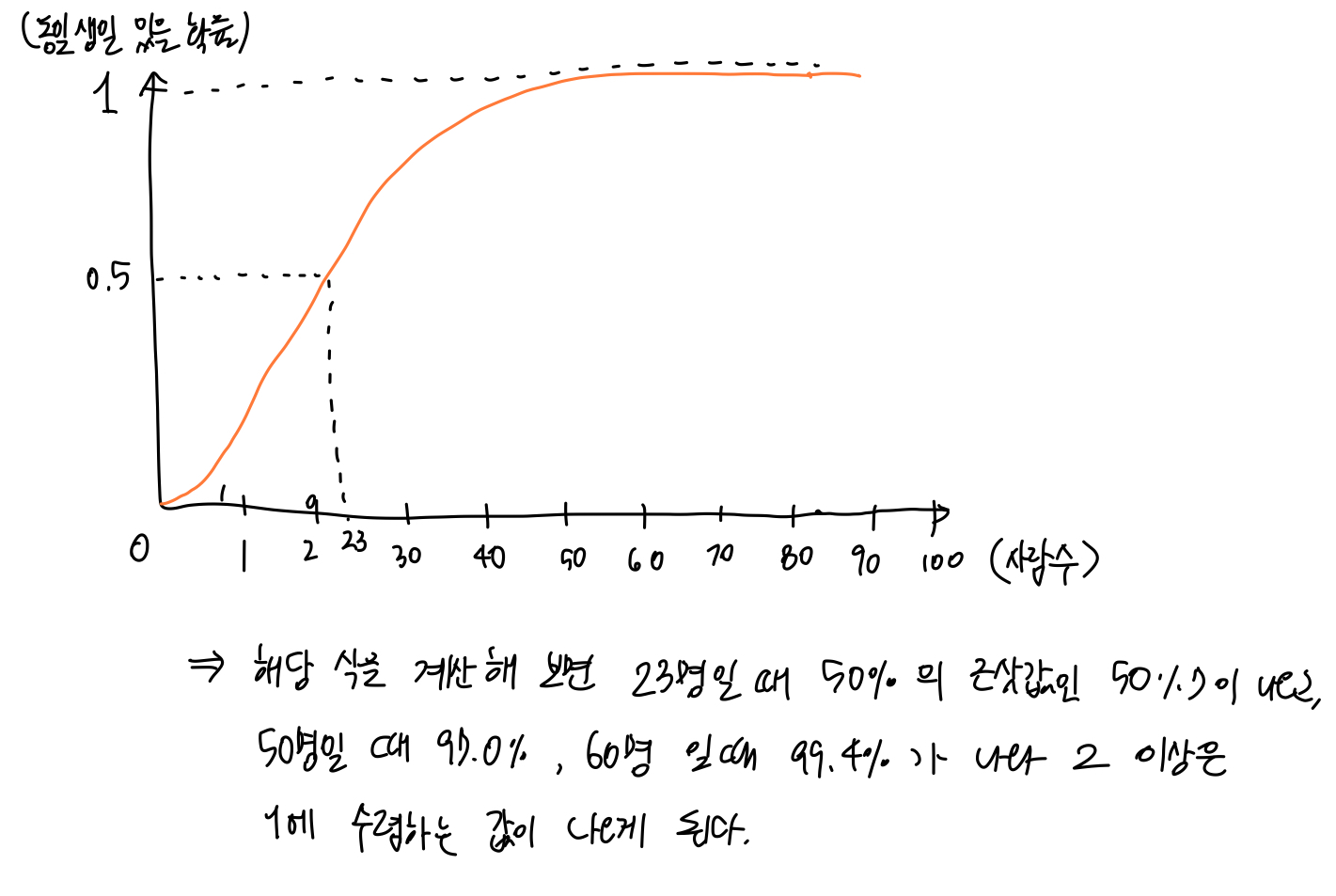
풀이: 1년을 365일이라 생각했을 때, 366명 이상의 사람이 모이면 무조건 생일이 동일한 한쌍이 생기게 된다. 그럼 우리가 생각해봐야하는 인원은 365명 이하의 인원이다.
p(n) = n명의 사람이 있을 때 그 중 생일이 같은 사람들이 한쌍 이상 있을 확률
~p(n) = 모든 사람의 생일이 다를 확률 (= 1 - p(n))

~p(n) = 1 x (1 - 1/365) x (1 - 2/365) x ... x (1 - n-1/365)
    = 365x364x363x...x(365-n+1)/365^n
    = 365!/365^n(365-n)!
    
따라서 p(n) = 1 - 365!/365^nx(365-n)!

수학적 귀납법을 사용하여 이 식의 정확성을 증명해보고자 한다.
수학적 귀납법의 진행 방식은 다음과 같다.
1. p(1)이 참이다.
2. p(n)이 참이면 p(n+1)도 참이다.
1, 2 모두 만족하면 모든 자연수 n에 대해 참이다.

이에 식을 대입해보면,
1. p(1) = 1 - 365!/365x364! = 0, 구성원이 한명인 집단에선 동일 생일자가 나올 수 없으므로 참이다.
2. p(n)이 참이라 가정하고, p(n+1) = 1 - 365!/365^(n+1)x(365-(n+1))! = 1- 365!/365^(n+1)x(364-n)! 도 참이다.
1, 2 모두 만족하므로 모든 자연수 n에 대해 참이라고 볼 수 있다.

코드:

import math

def p(n):
    result =  1 - math.factorial(365)/(365**n * math.factorial(365-n))
    return result

print(p(100))

그 결과는 아래와 같이 나왔다.