[python] 백준 1644 : 소수의 연속합

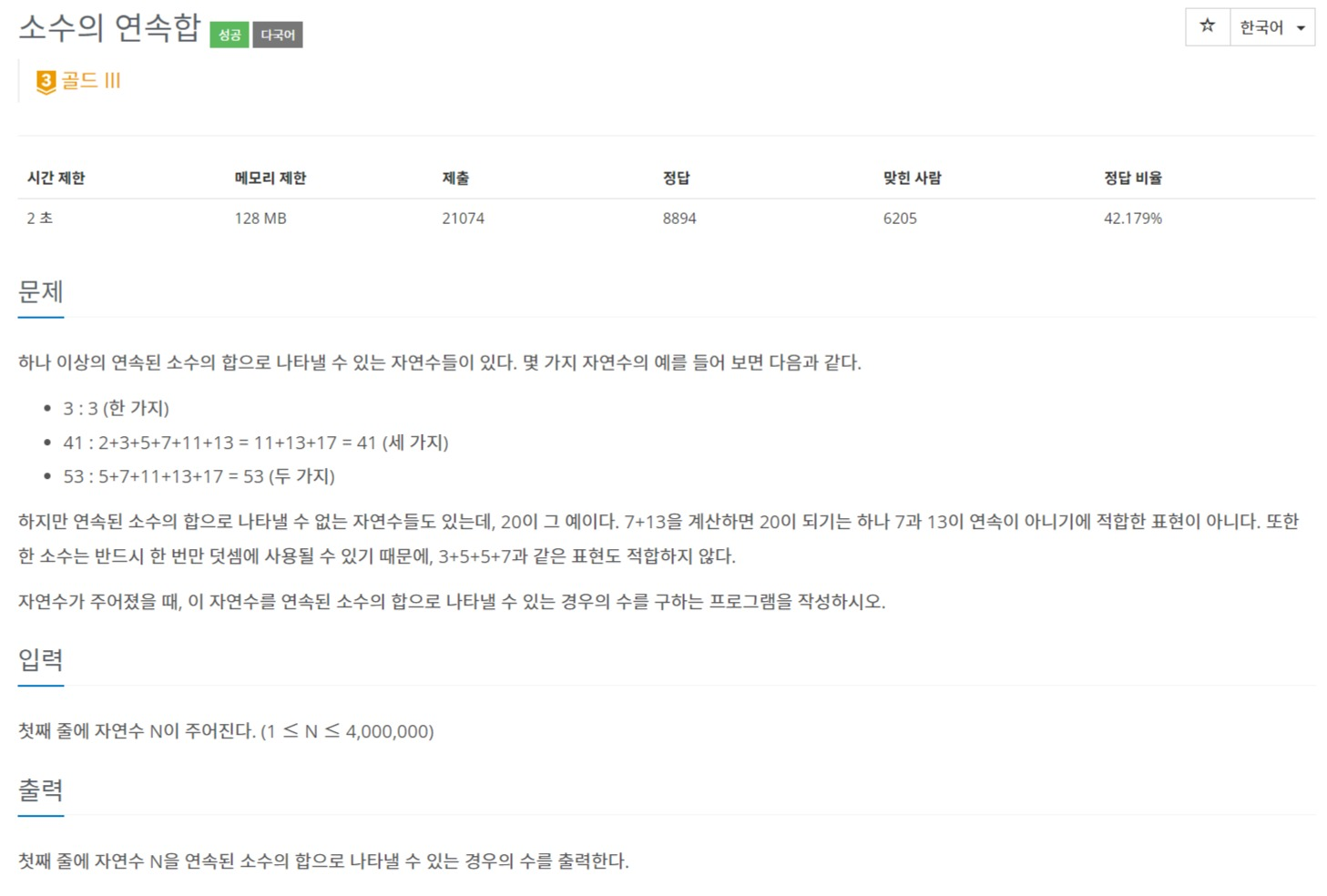
문제 링크
https://www.acmicpc.net/problem/1644

접근

일반적으로 내가 아는 소수 판별 알고리즘(√n 까지 탐색)으로는 시간초과를 피하지 못한다고 판단하여, 소수를 찾는 더 빠른 방법을 생각해야만 했다.
예전에 어디서 한번 봤지만, 제대로 알아보진 않았던 에라토스테네스의 체를 이용하여 소수를 알아내는 방법에 대해 알아보도록 하겠다.

소수 판별 (에라토스테네스의 체)

에라토스테네스의 체 위키백과

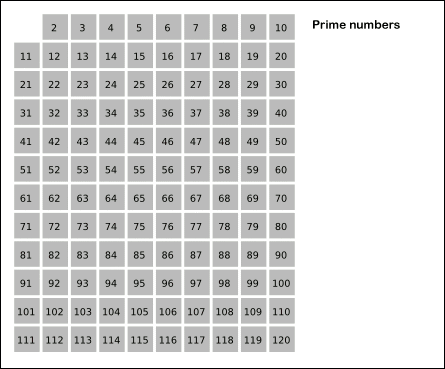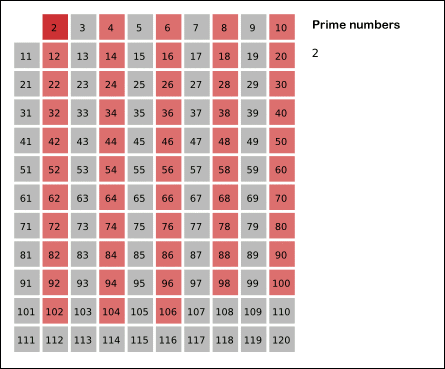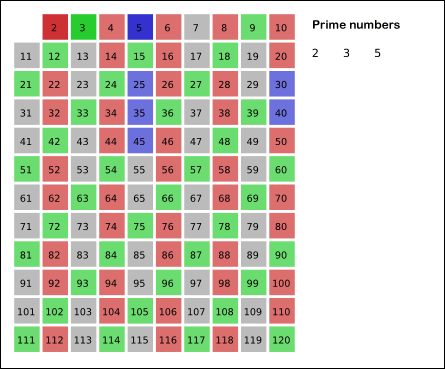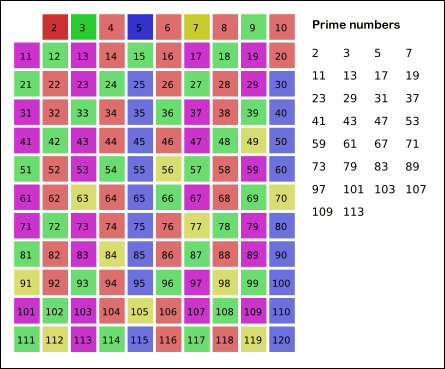
링크에 있는 설명을 정리하자면, 소수의 배수가 되는 수들은 소수가 아니므로 이를 미리 처리한다는 것이다.
이를 파이썬 코드로 구현한 것은 다음과 같다.

is_prime = [1 for _ in range(n + 1)]
is_prime[0], is_prime[1] = 0, 0

for i in range(2, int(math.sqrt(n)) + 1):
    if is_prime[i]:
        for j in range(2, n // i + 1):
            is_prime[i * j] = 0  # 소수의 배수들은 다 소수가 아니므로 0으로 만듦

먼저 n까지의 모든 수를 다 소수라고 생각하자. 예외로 0과 1은 소수가 아니므로 0이라고 설정해주자.
이제 2 이상의 수부터 소수인지 아닌지 확인한다. 만약 소수라면, 해당 수를 제외한 배수들을 전부 소수가 아니기 때문에 0을 넣어준다.

표현식을 for문으로 해서 그렇지 while문으로 하면 이해가 더 잘 될 것이다.

i = 2
while i * i <= n:
    if is_prime[i]:
        j = 2
        while i * j <= n:
            is_prime[i * j] = 0
            j += 1
    i += 1

풀이

이제 1부터 n까지의 수 중 어느 수가 소수이고 어느 수가 소수가 아닌지 알았으니, 소수만 따로 추출한다.

p = []
for i in range(2, n + 1):
    if is_prime[i]:
        p.append(i)

그리고 투포인터를 이용하여 연속된 소수 구간합을 구한다.
구간 합이 원하는 수보다 작으면 왼쪽 포인터를 왼쪽으로 한 칸 이동하여 구간 합을 늘려주고,
구간 합이 원하는 수보다 크면 오른쪽 포인터를 왼쪽으로 한 칸 이동하여 구간 합을 줄여준다.
만일 구간합이 원하는 수와 일치하면, 왼쪽 포인터를 왼쪽으로 한 칸 이동하여 구간합을 늘려준다. 어차피 다음 차례에 오른쪽 포인터를 이동시키게 되므로 상관이 없다.

cnt = 0
i, j = len(p) - 1, len(p) - 1
cur = p[-1]
while 0 <= i <= j and 0 <= j < len(p):
    if cur > n:
        cur -= p[j]
        j -= 1

    else:
        if cur == n:
            cnt += 1
        i -= 1
        if i < 0:
            break
        cur += p[i]

정답 코드

import sys
import math

sys.setrecursionlimit(10 ** 8)
input = lambda: sys.stdin.readline().rstrip()

n = int(input())
if n == 1:
    print(0)
    exit()

# 2 3 5 7 11 13 17 19 23 29 31 37 ...
# 4,000,000 == 2000^2
MAX = 4000000
is_prime = [1 for _ in range(n + 1)]
is_prime[0], is_prime[1] = 0, 0

for i in range(2, int(math.sqrt(n)) + 1):
    if is_prime[i]:
        for j in range(2, n // i + 1):
            is_prime[i * j] = 0  # 소수의 배수들은 다 소수가 아니므로 0으로 만듦

p = []
for i in range(2, n + 1):
    if is_prime[i]:
        p.append(i)

cnt = 0
i, j = len(p) - 1, len(p) - 1
cur = p[-1]
while 0 <= i <= j and 0 <= j < len(p):
    if cur > n:
        cur -= p[j]
        j -= 1

    else:
        if cur == n:
            cnt += 1
        i -= 1
        if i < 0:
            break
        cur += p[i]
print(cnt)