문제 링크
https://www.acmicpc.net/problem/1799
문제 이해
N-Queen 문제와 유사하다.
이번엔 대각선에 집중해야 하는데, 그것만 알면 반은 성공!
우선 그림과 같이 체스판을 대각선으로 생각하자.
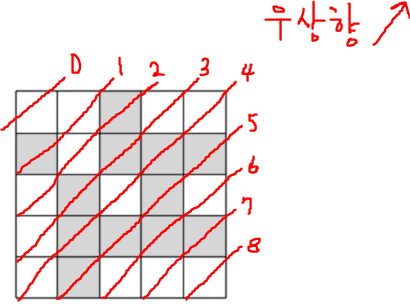
0번째 우상향 대각선은 (0,0)을 포함하는 대각선이다.
1번째 우상향 대각선은 (1,0), (0,1)을 포함하는 대각선이다.
...
4번째 우상향 대각선은 (4,0), (3,1), (2,2), (1,3), (0,4)를 포함하는 대각선이다.
...
- i 번째 우상향 대각선의 좌표는
y+x == i를 만족함
이런식으로 문제를 생각하도록 하자.
비숍의 특성상 한 우상향 대각선에는 한 개 이하의 비숍만이 놓일 수 있다.
그러므로 우상향 대각선의 개수만큼 순회하는 것을 생각해볼 수 있다.
다음은 우하향 그래프에 대해 생각해보자.
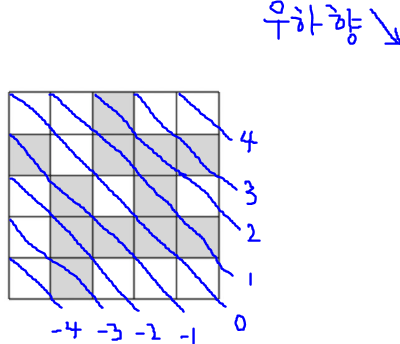
-4번째 우하향 대각선은 (4,0)을 포함하는 대각선이다.
-3번째 우하향 대각선은 (3,0), (4,1)을 포함하는 대각선이다.
...
0번째 우하향 대각선은 (0,0), (1,1), (2,2), (3,3), (4,4)를 포함하는 대각선이다.
...
4번째 우하향 대각선은 (0,4)을 포함하는 대각선이다.
- i 번째 우하향 대각선의 좌표는
x-y == i를 만족함- 코드는 다음과 같이 딕셔너리로 표현하였다.
rd = {} # 우하향(right down) 대각선 # 중앙 기준으로 쁠마 # (y,x) -> rd[x-y], 왼쪽 아래가 -(n-1), 오른쪽 위가 (n-1) for i in range(-n + 1, n): rd[i] = 0 # 초기화
우상향 대각선과 같이 한 우하향 대각선엔 하나 이하의 비숍만이 놓일 수 있다.
즉, 우상향 대각선당 비숍이 놓일 때 마다, 그 좌표에 해당하는 우하향 대각선을 체크하면 탐색 수를 크게 줄일 수 있다.
말이 좀 어려운 것 같은데, 코드를 보면 이해가 더 쉬울 것 같다.
접근 1 (only 백트래킹)
처음엔 그냥 백트래킹으로만 시도해보았다.
def f(diag, cnt): # diag 은 우상향 대각선의 번호. 첫 우상향 대각선이 0, 마지막이 2*n-2
global ans
if diag == 2 * n:
ans = max(ans, cnt)
return
for y in range(diag + 1): # 현재 대각선에서 가능한 y,x 조합 찾기
x = diag - y
if in_range(y, x) and board[y][x] and rd[x - y] == 0:
rd[x - y] = 1 # 현재 (y,x) 좌표에 비숍 넣었으므로, (y,x)가 속한 우하향 대각선 체크
f(diag + 1, cnt + 1) # (y,x) 좌표에 비숍 넣었으므로 cnt+1 하고 다음 우상향 대각선으로 감(diag+1)
rd[x - y] = 0이 방식은 복잡도가 대충 계산해보았을 때 O(n!n!) 이상이 나오는 것 같다. 사실 정확하진 않지만 아무튼 n이 커질수록 엄청나게 느려졌다.
접근 2 (백트래킹 + Branch & Bound)
def upper_bound(diag): # 현재 대각선(우상향) 위치에서부터 끝 대각선까지 뽑힐 가능성이 있는 애들의 갯수 반환
able_rus = 0 # 가능한 우상향 대각선들의 개수, 실제 가능하다기보단 단순히 가능할수도 있는 애들
for d in range(diag, 2 * n - 1):
for y in range(d + 1):
x = d - y
if in_range(y, x) and board[y][x] and rd[x - y] == 0:
able_rus += 1
break
return able_rus
def f(diag, cnt): # diag 은 우상향 대각선의 번호. 첫 우상향 대각선이 0, 마지막이 2*n-2
global ans
if diag == 2 * n:
ans = max(ans, cnt)
return
ub = upper_bound(diag) # 상한, 이번 대각선부터 끝까지 갔을 때 최대로 더 가질 수 있는 값
if ub + cnt <= ans: # 현재 cnt 값과 앞으로 최대한 얻을 수 있는 값을 더해도 기존 ans 보다 작으면
return # 빠져나온다
for y in range(diag + 1): # 현재 대각선에서 가능한 y,x 조합 찾기
x = diag - y
if in_range(y, x) and board[y][x] and rd[x - y] == 0:
rd[x - y] = 1 # 현재 (y,x) 좌표에 비숍 넣었으므로, (y,x)가 속한 우하향 대각선 체크
f(diag + 1, cnt + 1) # (y,x) 좌표에 비숍 넣었으므로 cnt+1 하고 다음 우상향 대각선으로 감(diag+1)
rd[x - y] = 0
f(diag + 1, cnt) # 이번 우상향 대각선에서 어떠한 좌표에도 비숍 넣지 않은 경우(cnt 그대로)
이번에는 연산 횟수를 줄이기 위해 상한을 두는 Branch & Bound 전략을 사용하보았다.
함수 upper_bound(diag)는 현재 우상향 대각선부터 마지막 우상향 대각선까지 "비숍 놓기가 가능할수도" 있는 대각선의 개수를 반환한다.
"비숍 놓기가 가능할수도" 라는 말에 특별히 강조를 한 이유는,
이 말이 실제로 가능한지 여부라기 보다는, "앞으로의 비숍 위치를 고려하지 않고 이전까지만의 비숍 위치만 고려한 정보이기 때문이다".
그러니까 upper_bound(diag) 호출 이전에 이미 놓여있는 비숍의 위치는 앞으로 가능 여부에 영향을 주지만, upper_bound(diag) 내에서 앞으로의 위치를 확인할 때는 상관이 없다는 것이다.
예를 들면,
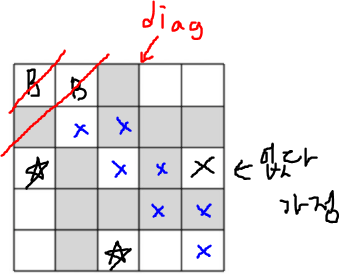
현재 우상향 대각선의 위치가 diag=3 이고, 비숍이 다음과 같이 놓여져있으면, x자 친것과 같이 저 영역에는 비숍을 놓을 수가 없다. (검은색 x는 설명을 위해 못 놓는 곳이라고 가정)
이 상황에서 앞으로 더 놓을 수 있는 비숍의 최대 개수는 "5개"이다.
별표친 부분에서 겹치므로 최대 4개가 아닌가 할수도 있지만, 함수 upper_bound(diag) 안에선 어디까지나 "가정"이다. 실제로 저 별표친 위치에 놓을지 안 놓을지 모르는 상황이고, 우리는 그냥 "최대한 많이"에 포인트를 맞추면 된다.
upper_bound(diag)함수의 목적은 실제로 비숍을 놓을 수 있는 최대 개수를 구하는 것이 아닌, 연산 수를 줄이기 위한 것이다.
정답 코드
import sys
sys.setrecursionlimit(10 ** 8)
input = lambda: sys.stdin.readline().rstrip()
in_range = lambda y, x: 0 <= y < n and 0 <= x < n
n = int(input())
board = [[] for _ in range(n)]
for i in range(n):
board[i] = list(map(int, input().split()))
rd = {} # 우하향(right down) 대각선
# 중앙 기준으로 쁠마
# (y,x) -> rd[x-y], 왼쪽 아래가 -(n-1), 오른쪽 위가 (n-1)
for i in range(-n + 1, n):
rd[i] = 0 # 초기화
def upper_bound(diag): # 현재 대각선(우상향) 위치에서부터 끝 대각선까지 뽑힐 가능성이 있는 애들의 갯수 반환
able_rus = 0 # 가능한 우상향 대각선들의 개수, 실제 가능하다기보단 단순히 가능할수도 있는 애들
for d in range(diag, 2 * n - 1):
for y in range(d + 1):
x = d - y
if in_range(y, x) and board[y][x] and rd[x - y] == 0:
able_rus += 1
break
return able_rus
def f(diag, cnt): # diag 은 우상향 대각선의 번호. 첫 우상향 대각선이 0, 마지막이 2*n-2
global ans
if diag == 2 * n:
ans = max(ans, cnt)
return
ub = upper_bound(diag) # 상한, 이번 대각선부터 끝까지 갔을 때 최대로 더 가질 수 있는 값
if ub + cnt <= ans: # 현재 cnt 값과 앞으로 최대한 얻을 수 있는 값을 더해도 기존 ans 보다 작으면
return # 빠져나온다
for y in range(diag + 1): # 현재 대각선에서 가능한 y,x 조합 찾기
x = diag - y
if in_range(y, x) and board[y][x] and rd[x - y] == 0:
rd[x - y] = 1 # 현재 (y,x) 좌표에 비숍 넣었으므로, (y,x)가 속한 우하향 대각선 체크
f(diag + 1, cnt + 1) # (y,x) 좌표에 비숍 넣었으므로 cnt+1 하고 다음 우상향 대각선으로 감(diag+1)
rd[x - y] = 0
f(diag + 1, cnt) # 이번 우상향 대각선에서 어떠한 좌표에도 비숍 넣지 않은 경우(cnt 그대로)
ans = 0
f(0, 0)
print(ans)
"""
10
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
"""