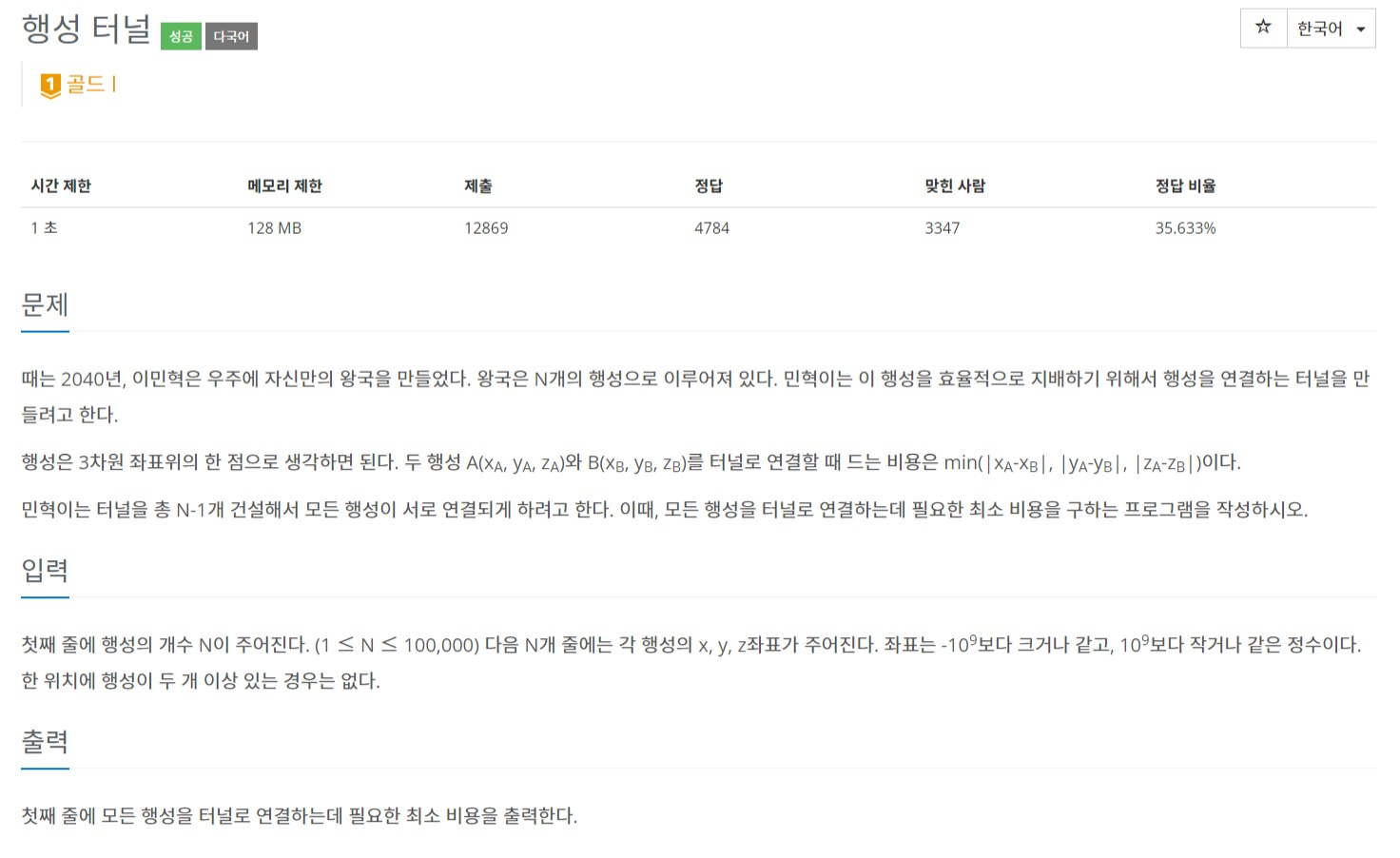
문제 링크
https://www.acmicpc.net/problem/2887
접근
N이 100,000으로 꽤 크다. O(N^2)의 시간복잡도가 안되므로, O(NlogN)의 복잡도를 갖는 알고리즘을 생각해보고자 하였다.
사실 처음에 딱 보고 최소신장트리로 풀어야겠다 생각했는데, 각 점(행성)마다 거리를 다 계산해버리면 O(N^2)이 나와버려 조금 막막했다.
이런 저런 시도도 해보았지만 잘 안 됐다. 그래도 시행착오 끝에 각 axis 마다 한번씩, 총 3회씩 연산해야될 것 같다는 감은 생겼다.
O(NlogN)의 복잡도를 갖는 알고리즘을 생각해보면, O(logN)의 과정을 N번 반복하는 것을 떠올렸다. 분할탐색을 하는 것은 아닌 것 같아서 우선순위큐나 힙을 이용하는 것을 생각했다.
풀이
일단은 처음엔 냅다 정렬 시켜보았다. 순서대로 x,y,z에 대하여 정렬한 것이고, 4번째 숫자는 행성의 번호(인덱스)이다.
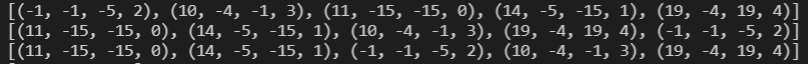
먼저 x에 대해서만 생각해보자.

x만 놓고 보았을 때 우리는 총 20의 비용으로 모든 행성을 이을 수 있다.
하지만 이건 우리가 원하는 답이 아닐 것이다.
이어서 y,z도 보자


해당 축에 대해서 가장 인접한 행성들끼리 모아놓은 것으로 볼 수 있다.
물론 이 자료를 적절히 이용하여 최소가 되게끔 하나의 연결된 트리로 만들어야 한다.
즉, 이 자료는 각 점마다 모든 점으로 가는 간선의 길이들에 대한 자료가 아닌, 강력한 후보군들만 모아놓은 자료들이라고 볼 수 있다.
이로써 필요한 간선들만 가져갈 수 있게 되어 시간을 절약할 수 있다(O(3N), 모든 간선 다 구하면 O(N^2)...)
가장 핵심인 알고리즘이다.
for i in range(n):
x, y, z = map(int, input().split())
planets[i] = (x, y, z, i)
xsort = sorted(planets, key=lambda x: x[0]) # x에 대하여 정렬
ysort = sorted(planets, key=lambda x: x[1]) # y에 대하여 정렬
zsort = sorted(planets, key=lambda x: x[2]) # z에 대하여 정렬
mh = [] # (len,a,b)
for i in range(n - 1):
heapq.heappush(
mh, (abs(xsort[i][0] - xsort[i + 1][0]), xsort[i][3], xsort[i + 1][3])
)
heapq.heappush(
mh, (abs(ysort[i][1] - ysort[i + 1][1]), ysort[i][3], ysort[i + 1][3])
)
heapq.heappush(
mh, (abs(zsort[i][2] - zsort[i + 1][2]), zsort[i][3], zsort[i + 1][3])
)우리는 최소힙에 (간선 길이, 점1, 점2) 형태의 자료를 넣을 것이다.
각 축에 대하여 인접한 두 점 사이의 거리와 두 점의 정보를 힙에 넣음으로 길이가 짧은 간선이 먼저 채택될 것이다.
그러면 최소신장트리를 만들 수 있다. 크루스칼 알고리즘을 사용하여 최소신장트리를 만드는 식으로 코드를 짰다.
정답 코드
import sys
import heapq
# sys.setrecursionlimit(10 ** 8) # pypy 제출시 삭제!
input = lambda: sys.stdin.readline().rstrip()
# in_range = lambda y,x: 0<=y<n and 0<=x<m
def find(v):
if v == root[v]:
return v
root[v] = find(root[v])
return root[v]
def union(v1, v2):
r1 = find(v1)
r2 = find(v2)
if r1 > r2:
r1, r2 = r2, r1 # r1 <= r2
root[r2] = r1 # 더 작은 인덱스가 root가 됨
n = int(input())
planets = [0 for _ in range(n)]
root = [i for i in range(n)]
for i in range(n):
x, y, z = map(int, input().split())
planets[i] = (x, y, z, i)
xsort = sorted(planets, key=lambda x: x[0]) # x에 대하여 정렬
ysort = sorted(planets, key=lambda x: x[1]) # y에 대하여 정렬
zsort = sorted(planets, key=lambda x: x[2]) # z에 대하여 정렬
mh = [] # (len,a,b)
for i in range(n - 1):
heapq.heappush(
mh, (abs(xsort[i][0] - xsort[i + 1][0]), xsort[i][3], xsort[i + 1][3])
) # x
heapq.heappush(
mh, (abs(ysort[i][1] - ysort[i + 1][1]), ysort[i][3], ysort[i + 1][3])
) # y
heapq.heappush(
mh, (abs(zsort[i][2] - zsort[i + 1][2]), zsort[i][3], zsort[i + 1][3])
) # z
cnt = 0
ans = 0
while cnt < n - 1: # 크루스칼 알고리즘
l, a, b = heapq.heappop(mh)
if find(a) != find(b):
union(a, b)
cnt += 1
ans += l
print(ans)