[python] 백준 6549 : 히스토그램에서 가장 큰 직사각형

문제 링크
https://www.acmicpc.net/problem/6549

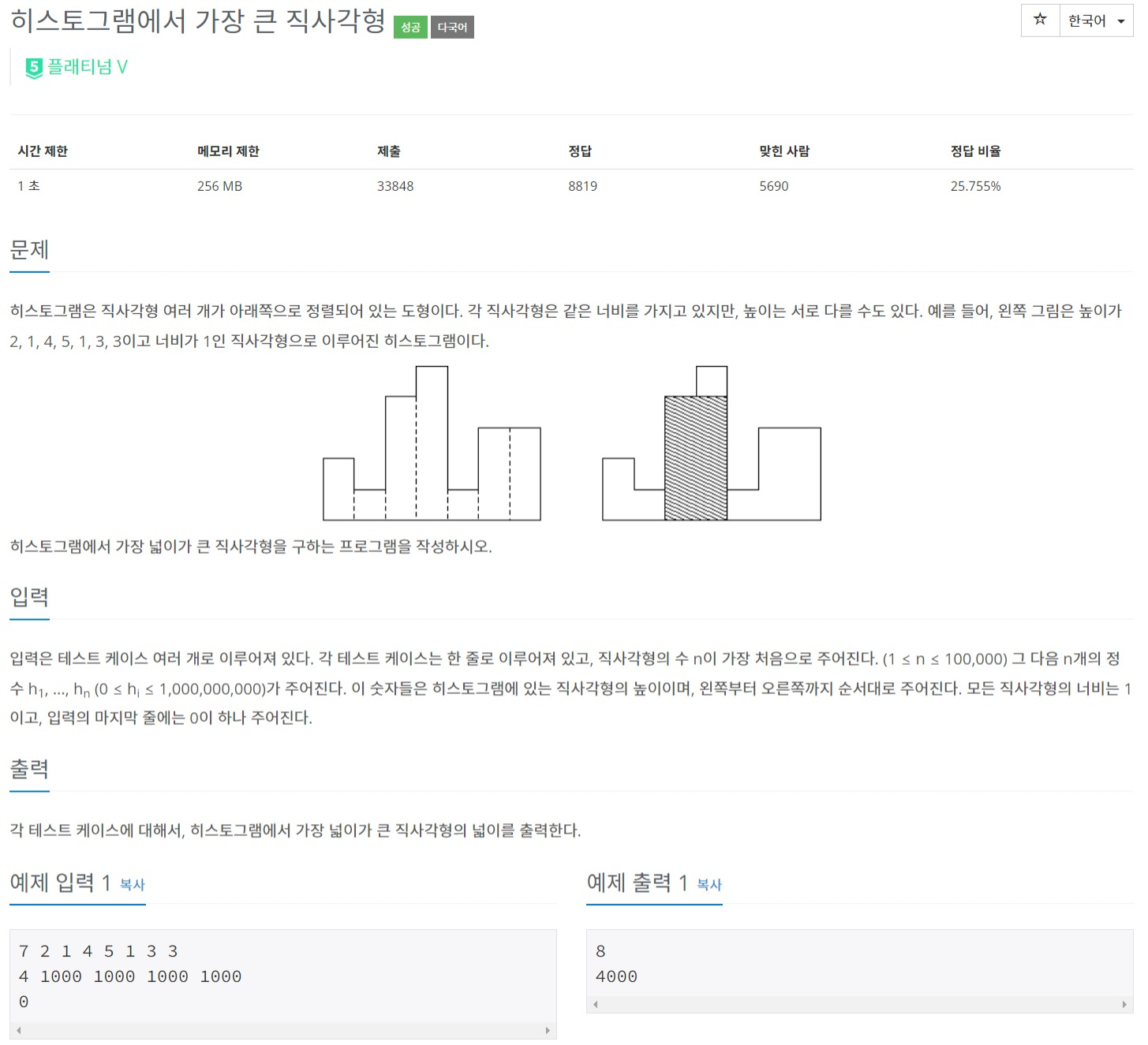
접근

주어진 n은 10만이고, 각 직사각형의 최대 높이는 10억이다. (높이로 뭐 할 생각 하지말자...)

시간 복잡도는 O(n^2) 보다는 좋아야 할 것이므로 분할하여 탐색하는 것을 생각했다.

문제를 보면 연속된 직사각형들의 넓이를 미리 구해놓는 작업을 하면 편해보인다. 따라서 세그먼트 트리를 이용한 접근을 생각했다.

풀이

이 문제에서 가장 큰 직사각형을 구하는 알고리즘은 다음과 같다.

1. 현재 구간을 반으로 쪼갠다.
2. 왼쪽 절반 구간에서의 가장 큰 직사각형과, 오른쪽 절반 구간에서의 가장 큰 직사각형의 크기를 재귀적으로 구한다.
3. 현재 구간에서, 아까 반으로 쪼갰던 경계 부분을 포함하는 가장 큰 직사각형의 크기를 구한다.
4. 셋(왼쪽 절반, 오른쪽 절반, 경계 포함)을 비교한다.

• 기본적으로 세그먼트 트리는 만들어놓자
• 세그먼트 트리는 각 구간의 최소 높이를 저장해놓은 트리로 설정했다.

---

위의 알고리즘을 코드로 구현하면 다음과 같다.

def f(frm, to):
    if frm == to:
        return histograms[frm]

    mid = (frm + to) // 2
    l = f(frm, mid)
    r = f(mid + 1, to)

    max_val = max(l, r)

    # including border
    h = min(histograms[mid], histograms[mid + 1])
    w = 2
    s = w * h
    i, j = mid, mid + 1
    while frm < i or j < to:  # i==frm and j==to 가 되면 종료
        if j == to or frm < i and histograms[i - 1] >= histograms[j + 1]:
            i -= 1
            w += 1
            h = min(h, histograms[i])
            s = max(s, w * h)
        else:
            j += 1
            w += 1
            h = min(h, histograms[j])
            s = max(s, w * h)

    max_val = max(max_val, s)

    return max_val

중앙인 mid를 기준으로 왼쪽, 오른쪽 구간으로 분할하여 재귀적으로 탐색한다. 그리고 현재 구간의 경계 부분을 포함하는 가장 큰 직사각형까지 구한다.

그리고 셋 중 가장 큰 값을 반환하는 함수이다.

추가적으로 경계 부분의 넓이를 구하는 방법은, 투포인터의 방법을 생각하면 된다.

처음에 i와j를 각각 mid, mid+1로 설정하고, 이 둘을 비교하며 높이가 더 큰쪽으로 이동하게끔 하는 것이다.

정답 코드

import math
import sys


# sys.setrecursionlimit(10 ** 8)  # pypy 제출시 삭제!
input = lambda: sys.stdin.readline().rstrip()
# in_range = lambda y,x: 0<=y<n and 0<=x<m
MAX = 1000000000


def make_seg(idx, s, e):
    if s == e:
        seg[idx] = histograms[s]
        return seg[idx]

    # w = e-s+1
    mid = (s + e) // 2
    l = make_seg(idx * 2, s, mid)
    r = make_seg(idx * 2 + 1, mid + 1, e)
    seg[idx] = min(l, r)
    return seg[idx]


def f(frm, to):
    if frm == to:
        return histograms[frm]

    mid = (frm + to) // 2
    l = f(frm, mid)
    r = f(mid + 1, to)

    max_val = max(l, r)

    # including border
    h = min(histograms[mid], histograms[mid + 1])
    w = 2
    s = w * h
    i, j = mid, mid + 1
    while frm < i or j < to:  # i==frm and j==to 가 되면 종료
        if j == to or frm < i and histograms[i - 1] >= histograms[j + 1]:
            i -= 1
            w += 1
            h = min(h, histograms[i])
            s = max(s, w * h)
        else:
            j += 1
            w += 1
            h = min(h, histograms[j])
            s = max(s, w * h)

    max_val = max(max_val, s)

    return max_val


while True:
    inp = list(map(int, input().split()))
    n = inp[0]
    if n == 0:
        break
    histograms = inp[1:]

    b = math.ceil(math.log2(n)) + 1
    node_n = 1 << b
    seg = [0] * node_n  # 구간의 min h 를 가짐
    make_seg(1, 0, len(histograms) - 1)

    print(f(0, len(histograms) - 1))