문제 링크
https://www.acmicpc.net/problem/9527
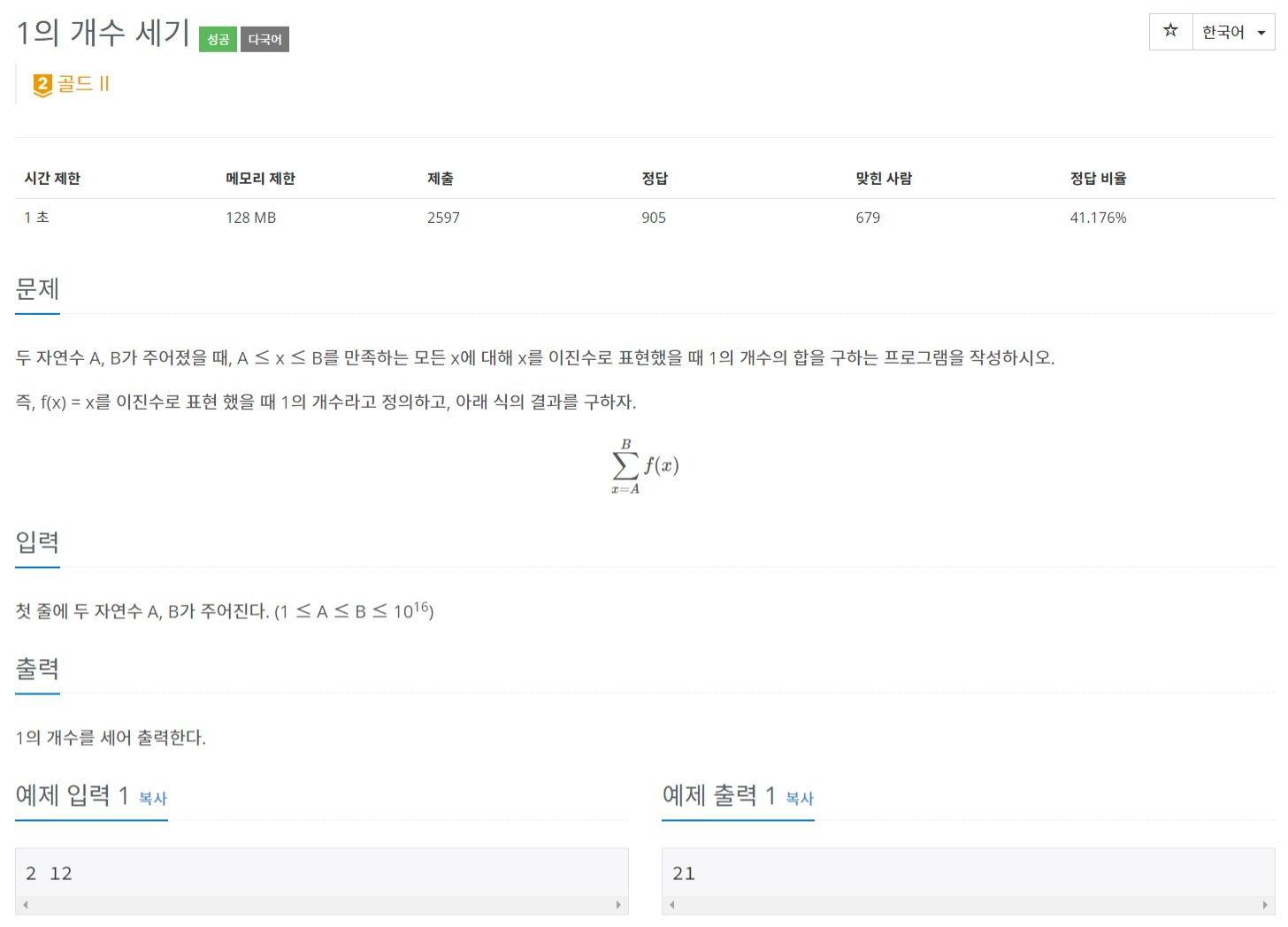
문제 이해
일단 처음에는 문제를 조금 쉽게 생각하고자 하였다.
주어진 식을 다음과 같이 변형시킬 수 있다.
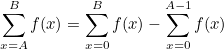
그렇다면 이제 저 식에서 0~K 까지의 f(x)합만 구하면 되는 것이다.
한편, N의 최대값이 무려 10^16으로 1경...O(N)으로도 해결이 불가능하다. (1부터 1경까지의 합을 구하는 것은 시간초과로 불가능!)
무조건 로그 시간복잡도를 생각해야하므로 분할정복을 생각해보았다.
풀이
중요한 점은 어떤 수를 이진수로 나타냈을 때 생기는 규칙성을 찾을 수 있어야 한다는 것이다.
결론부터 말하자면, 이 문제는 다음과 같은 규칙을 발견하면 쉽게 풀 수 있다.
- f(2ⁿ) = 1 이다. (항상 1000...0 이런 식이기 때문)
- 2ⁿ - 1 인 수들에 대하여 (1,3,7,15,31,...) 아래의 식이 성립한다.
2번에 주목해야 하는데, 예를 들어 설명하겠다.
사진 출처 : https://blog.naver.com/dsyun96/221843554389
위의 경우는 2⁴ - 1 = 15 인 경우이다 (n=4).
보는 것과 같이 첫째 자리 수(빨간색)의 경우 2의 주기로 0,1 이 반복되는 것을 볼 수 있고, 총 1의 개수는 8개 (2⁴ / 2 = 2³개)이다.
둘째 자리 수(파란색)의 경우 4의 주기로 0,0,1,1 이 반복되는 것을 볼 수 있고, 총 1의 개수는 역시나 8개이다.
셋째 자리 수 역시 1의 개수는 8개
마지막 넷째 자리 수 역시 1의 개수는 8개이다.
즉, 2ⁿ-1 인 수에서 무조건 각 자리수마다 1의 개수가 2ⁿ/2 개가 나온다는 것이다.
자리수는 총 n개 있으므로 2번 규칙의 식 n*2ⁿ/2 가 나오는 것이다.
좋다. 2의 제곱수에 대해서는 구할 수 있을 것 같다. 그런데 13과 같이 애매한 수는 어떻게 할 것인가?
답은 이 이진수들의 규칙성에 있다.
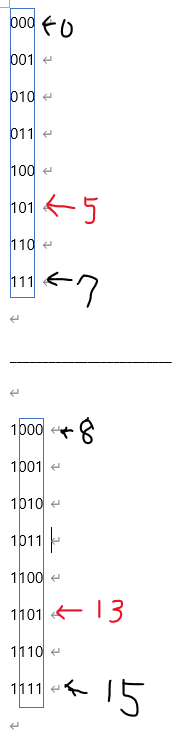
15를 반으로 쪼개어 보면 다음과 같다. 파란 박스에 들어가 있는 부분이 반복되는 것을 볼 수 있다.
13과 같이 애매한 숫자는, 절반에서 같은 위치에 있는 5를 보면 되는 것이다. 물론 8부터 13까지 총 6번의 1을 더해줘야 한다.
(근데 코드에선 2ⁿ을 기준으로 하여 9부터 13까지 총 5번의 1을 더해주고, 8은 그냥 새 함수를 호출하여 바로 리턴하는 식으로 짰다.)
def sum_f(x):
if x <= 0:
return 0
seung = int(math.log2(x)) # 2**seung <= x <= 2**(seung+1)
floor_2pow = 2 ** seung # <= x 인 2의 ?승
if floor_2pow == x:
return seung * x // 2 + 1
diff = x - floor_2pow
return sum_f(floor_2pow) + diff + sum_f(diff)코드를 설명하자면, 우선 seung 변수는 2의 ?승을 나타내기 위한 승이다. 발음 그대로 승이라고 했다.
x=13의 경우 2³ ≤ 13 ≤ 2⁴ 이므로 seung은 3이 될 것이다.
floor_2pow는 2**seung으로 x보다 크지 않은 2의 제곱수 중 최댓값, 즉 2³ ≤ 13 이므로 8이 된다.
이제부터 중요한데, 만일 x가 2의 제곱수이다? 그럼 아까 보았던 2번 규칙(2ⁿ-1 관련된거)를 참고하여 그것의 +1 해준 값을 리턴한다.
x가 2의 제곱수가 아닌 경우에는(13과 같이 애매한 경우),
그 수의 위치를 보기 위해 diff를 구하고(x와floor_2pow의 차이)
0부터 floor_2pow 사이의 수 중 0에서 diff 만큼 떨어진 수를 보는 것이다.(sum_f(diff))
그리고 아까 얘기했듯이 floor_2pow까지의 f(x) 합을 구하기 위해 sum_f(floor_2pow)를 더해주고, 차이인 diff도 더해준다.
정답 코드
import sys
import math
sys.setrecursionlimit(10 ** 8)
input = lambda: sys.stdin.readline().rstrip()
def sum_f(x):
if x <= 0:
return 0
seung = int(math.log2(x)) # 2**seung <= x <= 2**(seung+1)
floor_2pow = 2 ** seung # <= x 인 2의 ?승
if floor_2pow == x:
return seung * x // 2 + 1
diff = x - floor_2pow
return sum_f(floor_2pow) + diff + sum_f(diff)
# 2**53 < 10**16 < 2**54
# MAX = 10000000000000000
a, b = map(int, input().split())
print(sum_f(b) - sum_f(a - 1))
