수학에서의 실수는 유리수와 무리수를 통틀어 일컫지만, 컴퓨터, 프로그래밍에서의 실수는 보통 정수를 제외한 수를 가리킨다. JAVA에서는 실수를 float, double 두 가지의 비트로 제공한다.
이진법을 사용하는 컴퓨터에서는 정수에서의 가장 작은 단위인 1과 초깃값 0이 제공되므로 덧셈과 뺄셈으로 모든 정수를 정의할 수 있다. 하지만 실수는 1을 2로 계속 나눌 때마다 발생하는 소수들의 조합으로밖에 표현할 수 없다는 한계점을 지니고 있다. 따라서 컴퓨터 상에서 실수는 완벽하게 표현할 수 없고 최대한 근삿값에 가깝게 표현하려는 한계에 그칠 수밖에 없다.
우선 컴퓨터에서의 실수의 표현에 대해 알아보자.
실수의 표현 방식
23.628125의 이진수를 예시로 들어보자.
[정수부]
정수부의 2진수 변환은 간단하다. 정수를 2진수로 변환하면 끝이다. 정수부를 2로 나눈 나머지가 0이면 끝에서부터 0을 붙이고, 나머지가 1이면 1을 붙인 후 1을 빼주는 형식으로 풀어내면 1과 0으로 나타나는 2진수가 완성된다.
1) 23 = 11 x 2 + 1
2) 11 = 5 x 2 + 1
3) 5 = 2 x 2 + 1
4) 2 = 1 x 2 + 0
5) 1 = 0 x 2 + 1
- 23 -> 1 x (16) + 0 x (8) + 1 x (4) + 1 x (2) + 1 x (1) = 10111(2)
[실수부]
실수부의 2진수 변환은 역으로 2를 곱한다. 실수부에 2를 곱해 1보다 크거나 같으면 1을 반환 후 1을 빼고, 1보다 작으면 0을 반환 후 값을 유지한다.
1) 0.628125 x 2 = 1.25625 -> 0.25625 + 1
2) 0.25625 x 2 = 0.5125 -> 0.5125 + 0
3) 0.5125 x 2 = 1.025 -> 0.25 + 1
4) 0.25 x 2 = 0.5 -> 0.5 + 0
5) 0.5 x 2 = 1 -> 0 + 1
- 0.628125 -> 1 x (0.5) + 0 x (0.25) + 1 x (0.125) + 0 x (0.0625) + 1 x (0.03125) = 0.10101(2)
이 둘을 합친 값이 곧 실수 전체의 이진수이다.
23.628125 = 23 + 0.628125 = 10111(2) + 0.10101(2) = 10111.10101(2)
하지만, 앞서 예시로 든 23.628125는 2진수의 실수부를 유한하게 표현할 수 있는 숫자이고, 유한한 메모리로 표시할 수 없는 숫자가 있다.
예를 들면 0.1 = 0.00011001100....(0011).. 의 형태로 무한 반복을 하는 형태를 띈다. 이를 컴퓨터 메모리로 정확하게 표현하려면 무한한 메모리가 들어가게 되고, 결국 아무리 메모리를 써도 2진수로의 정확한 표현은 불가능하다.
double a = 0.17;
double b = 0.113;
System.out.println(a + b); // 기댓값 : 0.283
// 실제 : 0.28300000000000003...위처럼 두 소수를 더하면 0.283이 나와야 할 것 같지만 아래와 같은 근삿값이 나오게 된다. 그 이유는 2진법으로는 소수를 1을 2의 거듭제곱으로 나눈 소수들의 선형결합으로밖에 나타낼 수 없기 때문이다. 우리가 일반적으로 사용하는 것은 10진법이기 때문에 이를 완전히 나타내기란 어렵다. 사람들조차도 무한소수를 완전히 표현하지 못해 기호를 추가하거나 분수를 활용한다. 이처럼 2진법을 사용하는 컴퓨터에서도 나름 실수를 표현하는 방식이 존재한다.
고정소수점 방식
고정소수점 방식은 주어진 메모리를 정수부와 실수부를 위해 고정으로 나눈다.

(https://gsmesie692.tistory.com/94)
위는 16비트 메모리를 사용한 방식이다. 부호(양수 : 0, 음수 : 1)을 위한 1비트, 정수부 표현을 위한 7비트, 실수부 표현을 위한 8비트로 구성되어있다. 따라서 정수부는 -128 ~ 127까지 표현이 가능하다. 그리고 나머지 8비트로 실수부 표현을 하는데, 이진수로 표현된 실수부를 그대로 이 8비트에 넣게 된다.
고정소수점 방식은 말이 실수를 표현하는 방식일 뿐, 방식이 정수와 동일하기 때문에 구현이 간편하고 연산속도가 빠르다. 하지만 총 비트 대비 표현할 수 있는 수가 굉장히 한정적이다. n비트 사용 기준 최소 단위가 2^(- (n - 1) / 2) 정도로 상당히 큰 편이다.
부동소수점 방식
부동소수점 방식은 수를 표현하는 방법이 기존의 정수.실수 의 방식이 아닌 다음 형태로 사용한다.
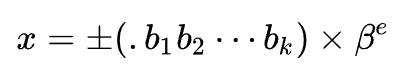
여기서 괄호 안을 가수부, e를 지수부라고 한다. 이 때 b1의 값이 0이 아니거나 가수부 자체가 0일 시 정규화되었다고 표현한다. 우리는 컴퓨터를 이용해 표현하기 때문에 2진수이므로 b는 0과 1로만 이루어져있고, beta는 2인 특수한 상황이다. 따라서 정규화된 부동소수점 형태는
23.628125 = 10111.10101(2) = +(0.1011110101) x 2^(5)(2)가 된다.
이렇게 정규화된 형태에서 부동소수점 방식은 메모리를 다음과 같이 분배한다.

위의 방식은 IEEE Floating Point Standard(IEEE 754)이며, 전지 전자 기술자 협회(IEEE)에서 개발한 컴퓨터에서 부동소수점을 표현하는 가장 널리 쓰이는 표준이다. 32비트 방식이므로 float에 해당한다.
부호 비트는 고정소수점 방식과 동일하며, 지수부는 8비트, 나머지 23비트는 가수부를 표현하는 데 사용된다. IEEE 754에서는 정규화를 할 때 실수부에 0을 남기는 것이 아닌 1을 남긴다. 따라서 위의 +(0.1011110101) x 2^(5)에서 자리수를 하나 올려 +(1.011110101) x 2^(4)로 표현된다. 이 상태에서
1) 부호 비트에 부호에 해당하는 수(양수 : 0, 음수 : 1)를 넣는다.
2) 지수부 비트에 (지수 + Bias)에 맞는 이진수를 넣는다.
3) 가수부 비트에 밑수에서 정수 쪽 1을 제외한 소수 부분을 채워넣고, 빈 공간은 0으로 채운다.
의 과정을 거친다.
- Bias
여기에서 Bias란 지수의 부호를 결정하기 위한 숫자이다. 지수부가 8비트이므로 -127 ~ 128의 256가지 숫자를 표현할 수 있는데, 이를 0을 기준으로 양수와 음수로 구분하기 위해 쓰인다. 8비트의 Bias는 127이므로 지수부의 0 ~ 126에는 음수를, 127에는 0을, 128 ~ 255에는 양수를 할당하는 것이다.
다시 돌아와 23.628125 = +(1.011110101) x 2^(4)를 부동소수점으로 표현해보자.
1) 양수이므로 부호 비트는 0(2)
2) 지수부 비트는 (지수 + Bias) = (4 + 127) = 131 = 10000011(2)
3) 가수부 비트는 밑수에서 정수 1을 제외한 011110101(2)에서 남는 자리를 0으로 채워 01111010100000000000000(2)
따라서 IEEE 754 방식에 따른 23.628125의 부동소수점 표현은
01000001101111010100000000000000(2)가 된다.( 1 / 10000011 / 01111010100000000000000 )
위는 float의 단정도(single precision, binary32)이며, double은 배정도(double precision, binary64)로 부호 1비트, 지수부 11비트, 가수부 52비트이다.
고정소수점 방식과 부동소수점 방식에도 각각 장단점이 있다. 고정소수점 방식은 표현할 수 있는 수의 숫자가 제한적이지만 그만큼 특정한 수의 계산에 있어서는 연산속도가 매우 빠르며 복잡도 또한 낮출 수 있다. 따라서 임베디드 분야나 반도체의 전기 신호를 다루는 등의 기계친화적인 분야에서 이용된다. 부동소수점 방식은 고정소수점 방식에 비해 연산 속도나 복잡도 면에서는 떨어질 수 있지만 표현할 수 있는 범위가 고정소수점 방식에 비해 압도적으로 넓기 때문에 극도의 고속, 고효율을 지향하지 않는 어플리케이션에서는 널리 이용되고 있다.
(참고자료 : https://gsmesie692.tistory.com/94)
