목차
1.행렬과 벡터 만들기
2.행렬 연산하기
3.행렬의 서브행렬 추출하기
4.그래프로 출력하기
1. 행렬과 벡터 만들기
배열(Array) = collection of scala values
vector(주로 소문자): n x 1 or 1 x n
matrix(주로 대문자) : n x m
ex) row vector, column vector, matrix
r = [1 2 3 4]
c = [1; 2; 3; 4;]
m = [1 2; 3 4;]
1) 다양한 방법으로 행렬 만들기
-대괄호사이에 원소 하나하나 써주기, ;는 열바꿈
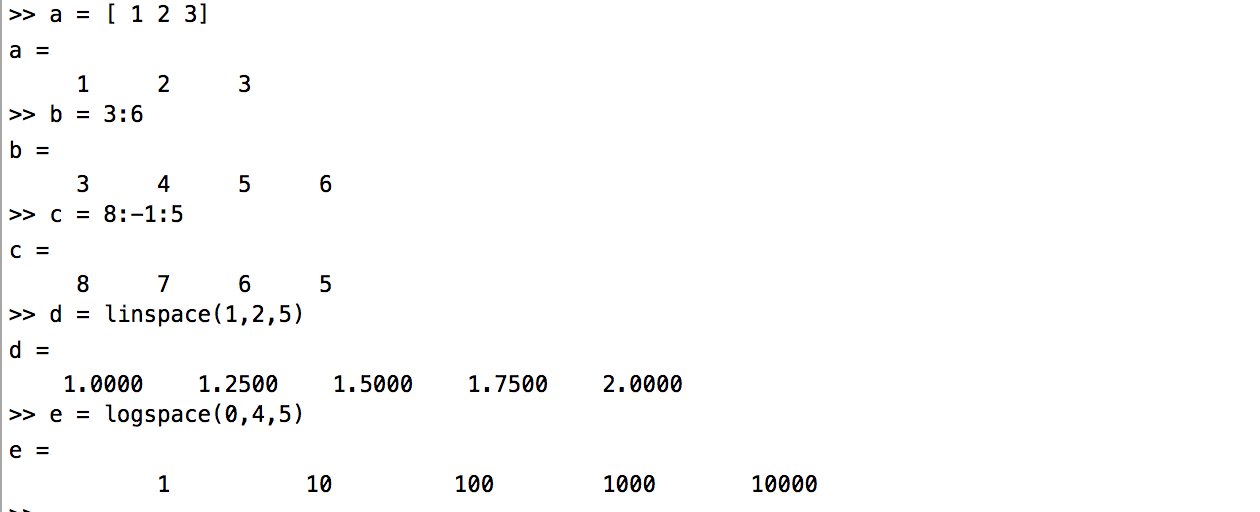
-대괄호 사이에 시작:끝, 시작:간격:끝 범위 써주기, 1만큼 크기의 원소들이 자동으로 행방향으로 채워진다.
-linspace(시작,끝,n등분) : 시작과 끝의 범위를 n간격으로 linear scale로 만들어준다
-logspace(시작,끝,n등분) : log스케일로 만들어준다.
2) Array Addressing
ex)
a=[0:0.2:1]이라는 Array를 생성했을때 인덱스는 총 1 부터 6이된다.
이때 a(addressing_syntax)를 통해서 원래 행렬에 다양하게 addressing할 수 있다.

2. 행렬에 사용할수있는 내장함수
a = [1 2 3; 4 5 6;] 일때
s = size(a)
[m, n] = size(a)
m = size(a,1) // row의 수
n = size(a,2) // col의 수
l = length(a) // row col 중에 긴 수
e = numel(a) // number of element
3. 특수행렬 만들기
✔️ Ones and Zeros
a= ones(2) //k로 채워진 행렬을 만들때 유용
c = zeros(3) //초기화에 유용

✔️Identity matrix
I = eye(5)
✔️Diagonal Matrix
a = 1:3
b = diag(a)
b = diag(a,1) //offset 대각선을 오른쪽으로 한칸 이동
b = diag(a,-1)

4. 부분행렬 구하기
M(n, :) //n-th row
M(m:m, :) //m~n-th rows
M( :, r) //r-th col
M( :, r:s) //r-th cols

5. 행렬의 연산
scalar operation & matrix operation
.*, ./, .^ 각각의 위치에 해당 연산을 수행
복소수와 켤레복소수
복소수에 트랜스포즈를 취하면 트랜스포즈와 켤레복소수가 구해진다. (./ = 켤레복소수만 구해준다)
