MATLAB 뿌셔뿌셔 7. 다항식 계산하기

공대생에게 가장 유용한 매트랩 기능 중에 하나인 다항식 계산에 대해 알아보자.

목차
0. 주석으로 다항식을 작성하는 방법 - LaTex
1. 다항식을 매트랩에서 array로 표현하는 방법
2. 다항식 계산하기

1. 다항식 (Polynomials)을 array로 표현하기

• 다항식이란 항이 여러개로 이루어진 식

• 매트랩에서는 최고차항부터 계수를 array에 담아서 표시한다.

  ex) f(x) = 5x^5 + 6x^2 + 4x +2 => p = [5 0 0 6 4 2]

2. 다항식 계산하기

1) 다항식의 값 구하기 (x값에 대한 y값)

% 다항식 p에서 x의 값에 해당하는 y값

y = polyval(p,x);

ex) f(x) = 5x^5 + 6x^2 + 4x +2 그래프 그리기

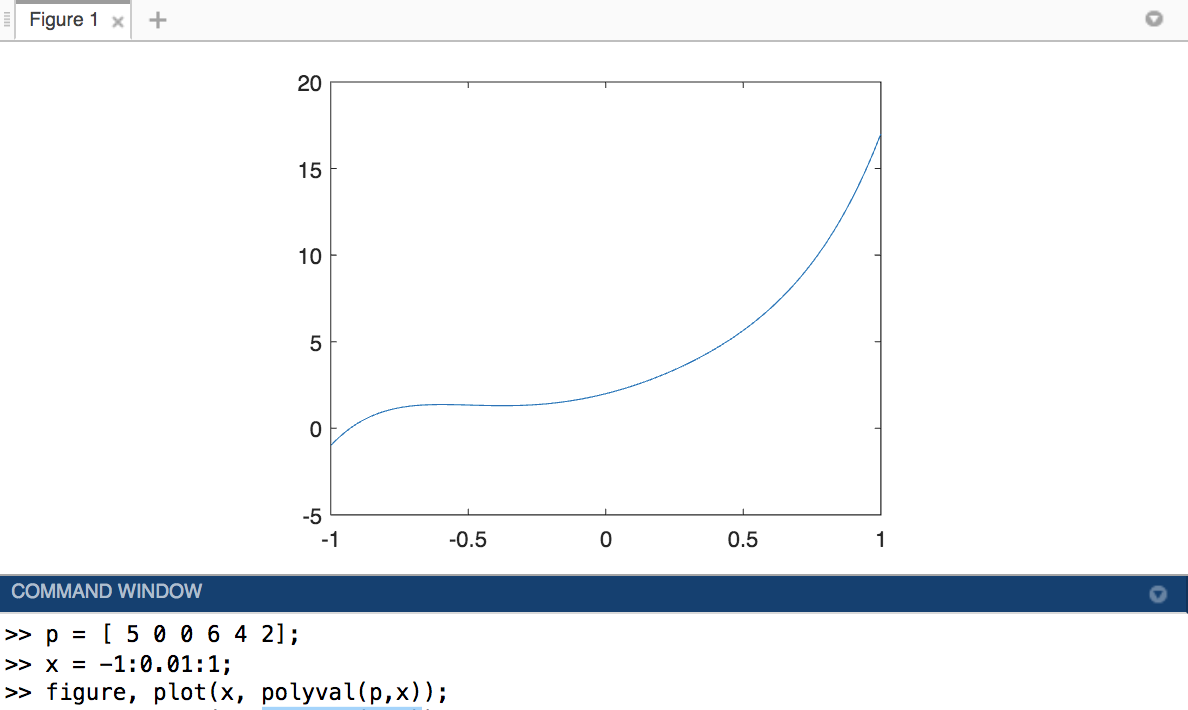
2) 다항식의 근 구하기 (y가 0이 되는 x값)

r = roots(p); % 다항식 p의 근을 구해주는 함수 

p = poly(r); % r을 가지고 다항식을 구해주는 함수 

ex) 다항식 곡선과 근 나타내기

f(x) = (x+1.2)(x+0.6)(x-0.1)(x-1.9)

step1. 근 알아내기
step2. 다항식 계수 표현하기

r = [-1.2 -0.6 0.1 1.9];

step3. 곡선의 x좌표 나타내기

x = linsspace(-1.5, 2, 1000); % -1.5 부터 2 사이를 1000등분하기 

step4. 곡선의 y좌표 나타내기

p = poly(r);
y0 = polycal(p, r); % r에서의 y값 == zeros(size(r));
y = polyval(p, x);

step5. 그래프 그리기

plot(x, y)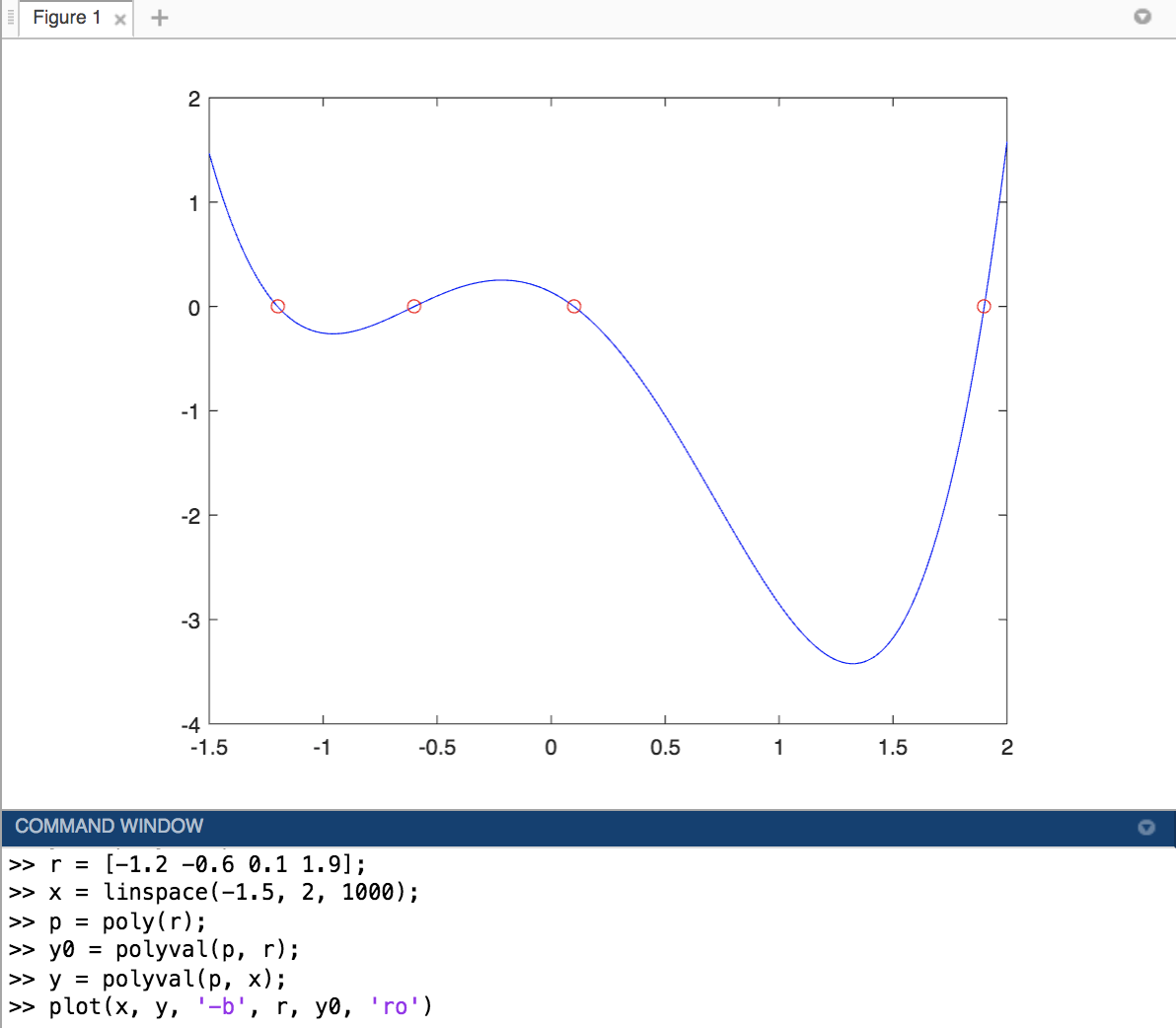

3) 다항식의 곱과 나누기 계산하기

f(x)를 p1, g(x)를 p2로 나타낸 뒤

r = conv(p1, p2); % r(x) = f(x)g(x)

[q, r] = deconv(p1, p2)  %q= 몫, r=나머지

4) 다항식 미분

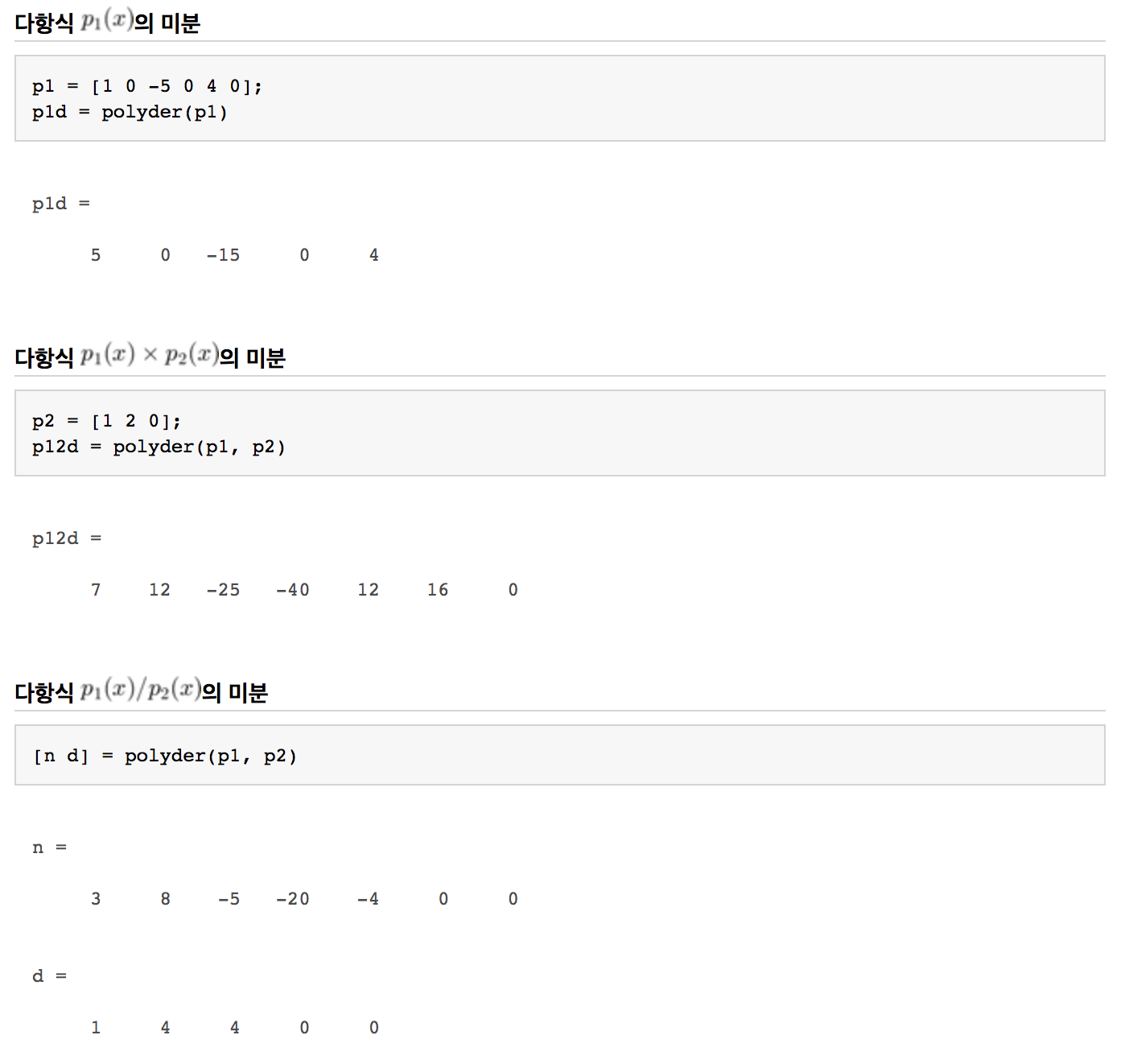
5) 다항식의 최대 최소

ex1) 다항식 f(x) = (x+1.2)(x+0.6)(x-0.1)(x-1.9), x = -1.5 ~ 2 의 범위에 대하여 $f(x)$의 그래프를 그리고, local maximum과 local minimum을 함께 나타내시오.

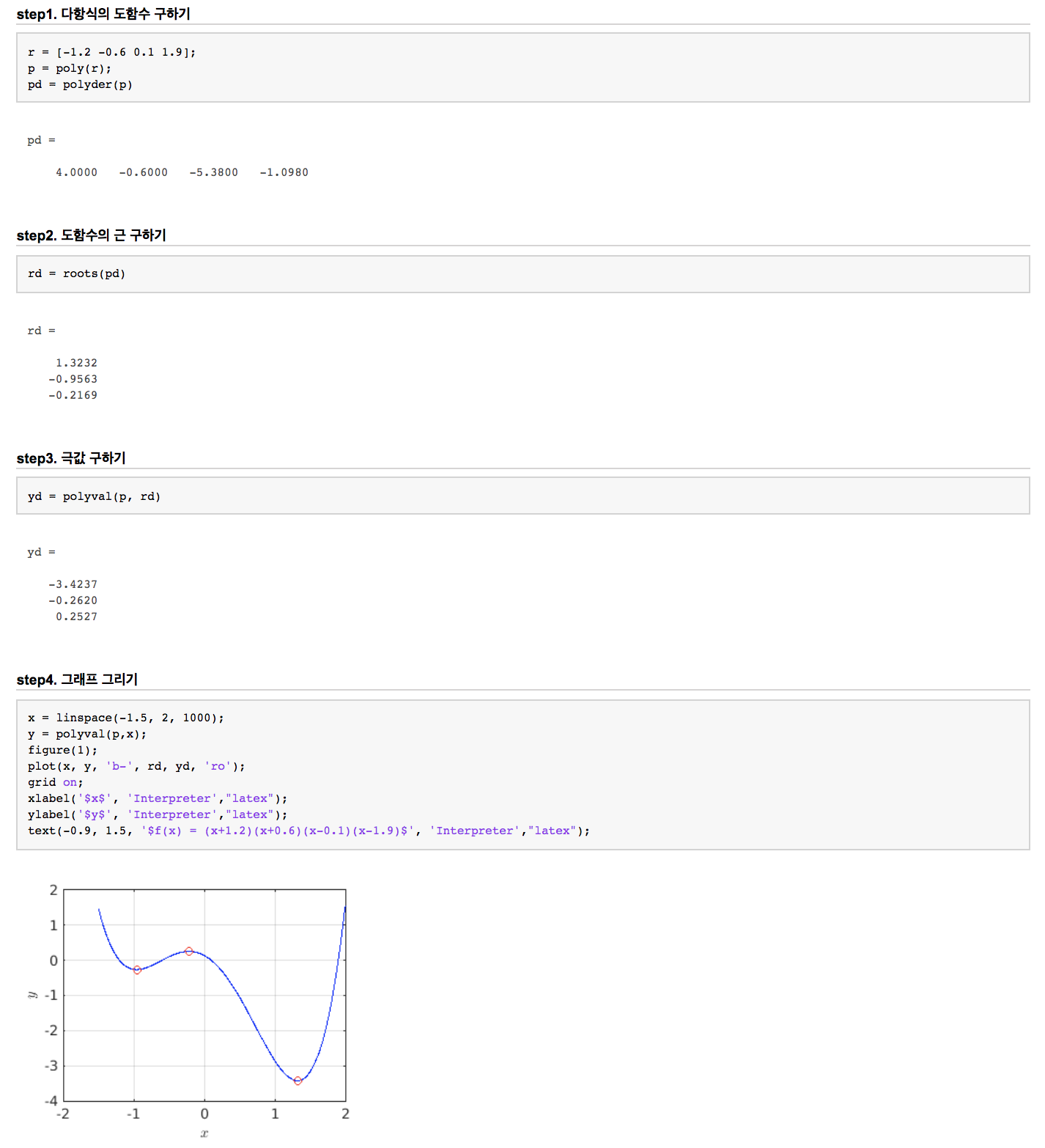
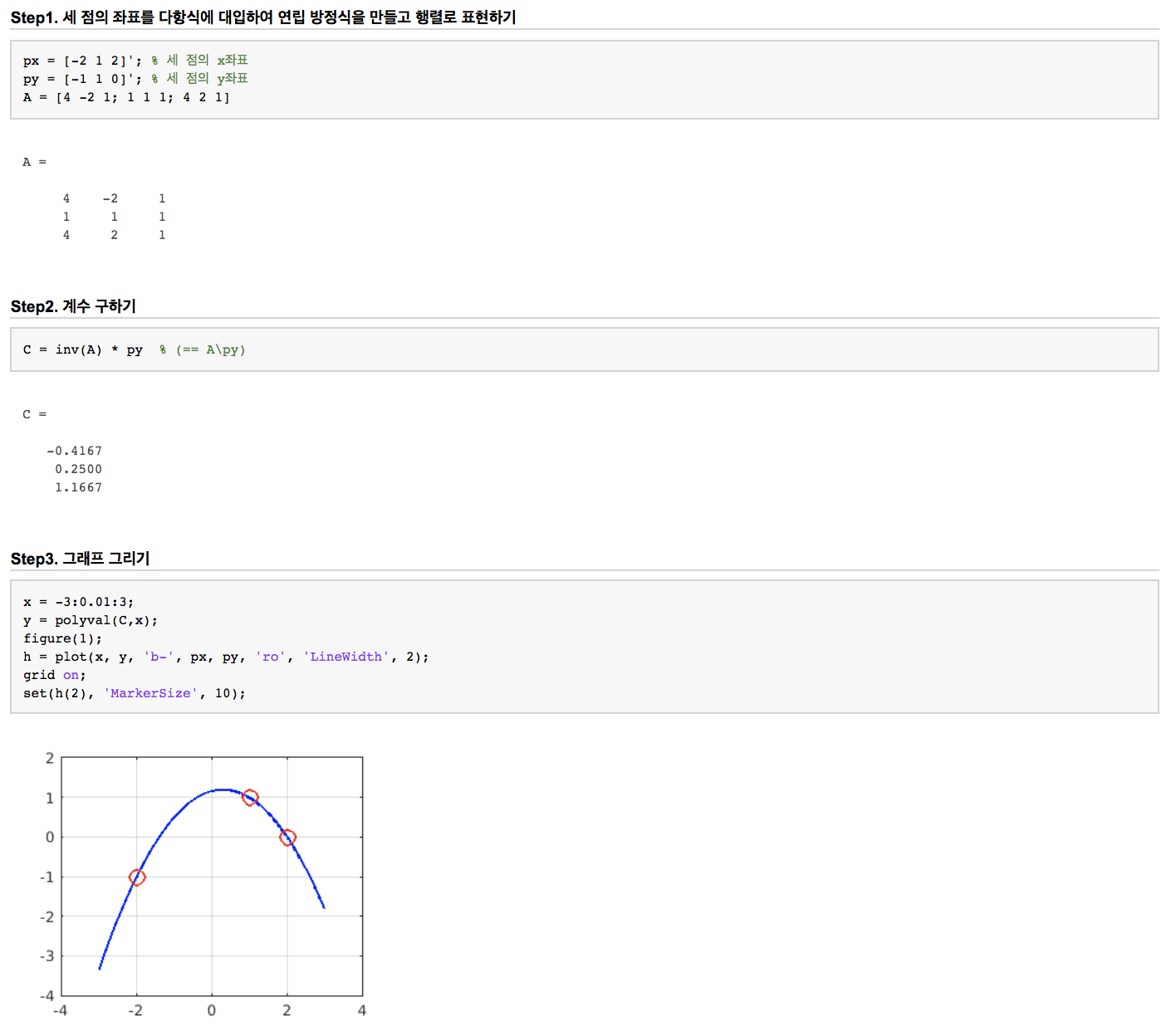
ex2) 세 점 p1(-2,-1), p2(1,1), p3(2,0)을 지나는 이차방정식의 계수를 구하여라.

sol: y = ax^2 + bx + c에 각각의 점을 대입한 연립방정식의 해를 구한다.