Problem

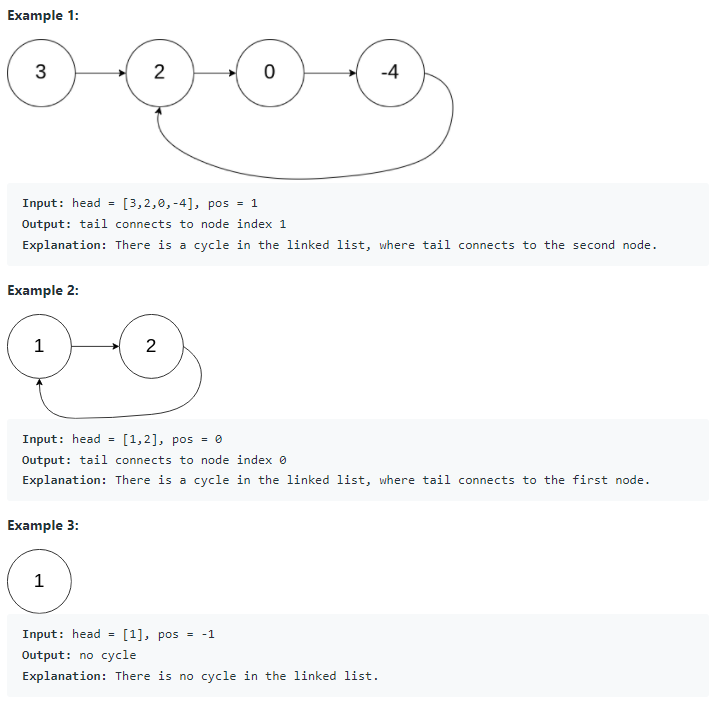
Problem: https://leetcode.com/problems/linked-list-cycle-ii/

아무 생각없이 풀 땐 계속 unordered_set에 저장하면서 next로 이동하다가 nullptr이 나오면 no cycle, 똑같은 node를 만나면 cycle 시작점 이렇게 답을 구했는데 구하고 보니 follow up이 O(1) memory 로 구하시오였다... 이런, 모르겠다!

Approach

2개의 pointer로 cycle 여부와 cycle 시작점을 알아낼 수 있다!

Simple Explanation

1) 1번 pointer는 head부터 시작해서 1개씩, 2번 pointer는 head부터 시작해서 2개씩 next로 간다
2) 1번 pointer와 2번 pointer가 만나면
3) 2번 pointer를 다시 head 부터 시작해서 이제부턴 1,2번 pointer 모두 1개씩 next로 간다
4) 1,2번 pointer가 만나는 지점이 cycle의 시작점이다

Why?

1번 pointer가 n만큼 갔을 때 (=2번 pointer는 2n만큼 갔을 때) 2번 pointer와 만난다고 하자. 1번과 2번 pointer가 만났다는 것은 (2n - n = n) 만큼 갈 때마다 제자리로 돌아온다는 것이므로 cycle의 node의 갯수가 n개의 약수라는 것을 뜻한다
이 때 2번 pointer를 head부터 다시 시작하여 x만큼 더 이동하면 (head부터 cycle 시작점까지의 node의 갯수를 x라고 하자), 1번 pointer는 원래의 자리 n에서 x만큼 이동하여 전체 x + n 만큼 이동한 것이 된다. x(cycle 시작점)에서 n만큼 이동하면 제자리로 돌아오게 되므로 2번 pointer와 만나게 된다.

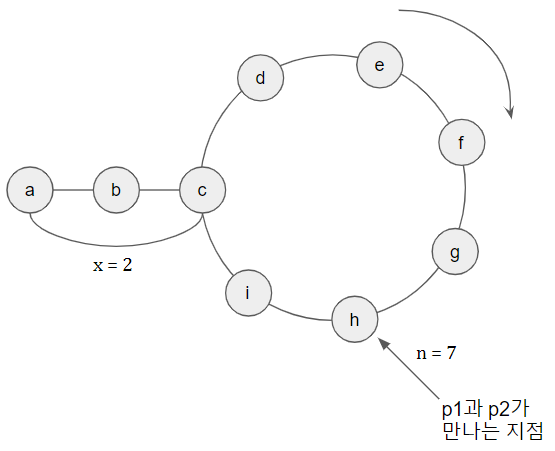
위와 같이 그림 예시를 들면 이해가 좀 더 쉬웠다. p1이 7만큼, p2가 14만큼 가서 h 노드에서 만나면 (n = 7), p2를 a로 이동시켜서 a->b->c로 오는 동안 p1이 h->i->c로 움직여서 p1과 p2가 cycle 의 시작점인 c에서 만난다!

Complexity

1) Time

O(n)

2) Space

O(1) 의 공간복잡도를 가진다