Train a Neural Network in TensorFlow
->x는 이미지를 의미.
입력 이미지 -> 25-> 15(여기까지는 은닉층)-> 1개(출력층)이 있을 때
X(이미지), Y(정답 셋)이 주어져 있다면, 이를 가지고 신경망을 구성하는 데 사용될 수 있는 매개변수 훈련 방법을 어떻게 익힐 수 있는가?
Tensorflow 활용
import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
model = Sequential([
Dense(units=25, activation='sigmoid'),
Dense(units=15, activation='sigmoid'),
Dense(units=1, activation='sigmoid'),
])
from tensorflow.keras.losses import BinaryCrossentropy
model.compile(loss=BinaryCrossentropy()) # 손실함수 지정.
model.fit(X,Y, epochs=100) #epochs -> 경사하강법에서 실행할 Step 횟수=> 1단계 모델 설정 및 지정, 2단계 손실 함수 선택, 3단계 손실 함수가 최소화되도록 데이터를 fitting하여 학습.
Training_Details
- 입력 특성 x과 매개변수 w,b가 주어졌을 때 아웃풋을 어떻게 계산할 수 있는가? (모델 설계)
# logistic regression
z = np.dot(w,x) + b
f_x = 1/(1+np.exp(-z))- 손실과 비용을 특정함.
loss = -y * np.log(f_x) - (1-y) * np.log(1-f_x)손실 : 단일 훈련 예제에서 로지스틱 회귀가 얼만큼 잘 수행되었는지 측정하는 것. -> 이렇게 손실 함수가 정의된다면, 모든 훈련 자료에서 각각 loss가 구해지고 이를 평균낸다면 그것은 '비용함수'임.
- w,b의 비용함수를 경사하강법으로 최소화함.
w = w - alpha * dj_dw # dj_dw 값은 편미분 값
b = b - alpha * dj_db- Tensorflow에서의 상황
1단계. model 구성 (sequential 활용하여 모델 구성)
2단계. binary cross entropy 이진교차 손실 함수를 통해 손실 함수를 지정. -> 모든 자료에 대한 손실 함수 값 평균이 비용.
model.compile(loss=BinaryCrossentropy) #이진 분류 시
Regreesion(회귀) 작업 시에는 model.compile(loss=MeanSquaredError()) 사용.
3단계. 비용이 최소화되도록 모델 학습 -> model.fit()
y는 타겟, f(->x)는 신경만에서 예측한 값.
정리하자면
y = target
f(->x) = prediction
binarycrossentropy -> 이진 분류 시 많이 쓰임.
비용함수를 최소화하기 위해 경사하강법 실행 시 각 유닛에 대한 모든 w,b를 Update하는 방향으로.
Alternatives to the sigmoid Activation
수요 예측 예시와 같이 이진법으로 나타내는 것이 최고의 방법이 아닐 때 생각해봄.
대안 1. ReLU -> z가 음수면 0, z가 0 이상일 때 g(z) = z
(Rectified Linear Unit)
대안 2. Linear Activation function -> 활성화 함수가 사용되지 않았다. 그렇지만 이 클래스에서는 선형 활성화 함수를 사용했다라고 한다.
Softmax Activation -> 다진 클래스 진행할 때 사용.
Choosing Activation Functions
마지막 출력층(결과값) -> 활성화 함수의 결과값
Binary Classification -> Sigmoid 함수가 적합.
Regression (양 음수 모두 있는 경우) -> Linear Activation Function 함수가 적합.
Regression 중 0 또는 양수의 값 -> ReLU 함수가 적합.
은닉층에 대한 활성화 함수는 ReLU를 가장 많이 사용함. (중요)
이진 분류에 대한 것만 Sigmoid 함수 사용.(예외 사항 파악하기)
ReLU가 sigmoid보다 더 좋은 이유
1. ReLU는 0까지만 flat하고 양수는 flat한 부분임.
2. Sigmoid는 0쪽 부분 제외 모두 flat(평평)함.
=> flat한 부분은 그라디언트가 작게 나타나기에 수렴하기에 많은 시간이 소요됨.
Why do we need Activation functions
모든 뉴런에 선형 활성화 함수를 사용하면 왜 작동하지 않는가?
=> 복잡한 모델에 적합화시키기 위해 큰 신경망을 쓴 것이 단순한 모델을 가진 선형 회귀 문제와 전혀 다른 게 없어서 복잡한 모델을 사용한 이유가 없어지기 때문.
"특히 은닉층에서 선형 활성화 함수를 쓰면 안 된다! ReLU를 사용할 것"
Multiclass Classification
Example 1. 0~9까지의 손글씨 인식 문제.
=> Target y는 두 개 이상의 가능한 값을 가질 수 있음.
확률적인 값으로 그래프에 나타남. (2진 분류와 같이)
Softmax Function
a1 => y=1의 값을 가질 확률
a2 => y=2의 값을 가질 확률
a3 => y=3의 값을 가질 확률
a4 => y=4의 값을 가질 확률
z1 = ->w1 * ->x + b1
a1 = e^z1/e^z1+e^z2+e^z3+e^z4
Cost Function
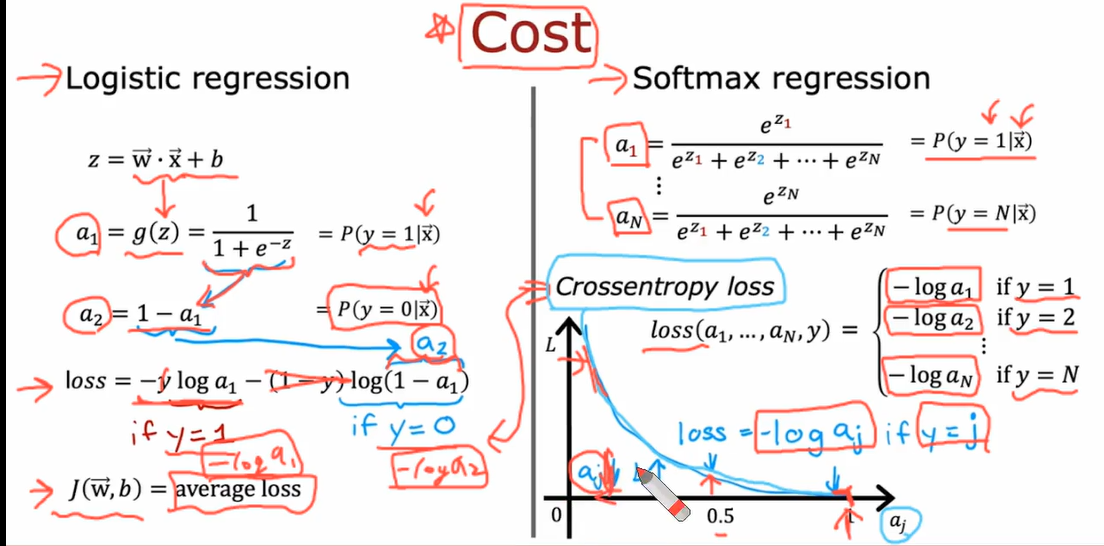
softmax 함수에서는 activation 값이 1에 가까울 수록 최적화가 잘 된 것.
Neural network with softmax output
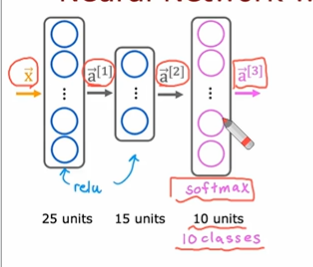
10개의 z값을 계산해야 함. -> 그리고 그 값을 이용해서 a값을 계산.
로지스틱 회귀에서는 activation 함수가 하나의 z값에 대해 영향을 받지만
softmax에서는 여러 개의 z값이 같이 얻어져야 계산할 수 있음.
improved implementation of softmax
발생할 수 있는 에러
1. Numerical Roundoff Errors (수치 반올림 오류)
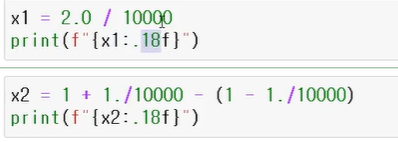
숫자를 저장하는 바이트 수가 한정되어 발생하는 오류
softmax 함수에서는 여러 계산들이 복합되어 진행되기 때문에 수치 반올림 오류가 발생할 확률이 높아야 함.



위의 사진 방식대로 해결하면 됨.
Predict에서

linear로 먼저 진행하고 tf.nn.~로 확률값으로 바꿔주어야 함.
logit = model(X)는 a값이 아닌 z값임!
Classification with multiple outputs
(다중 레이블 분류 문제)

예시.
고로 y = [1 0 1] (세로 방향의 벡터)로 출력될 수 있다는 것.
네트워크를 여러 개 두고 하나에 하나만 감지할 수 있도록 하는 방법보단
하나의 네트워크를 두고 출력값을 3개 노드로 주는 방법으로.(각각 활성화 함수를 sigmoid로)
*이는 다중 클래스 분류와는 전혀 다른 문제임!
