
구종만님의 "프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략"을 기반으로 공부한 내용입니다.📚 목차
1. 도입
2. 문제: 쿼드 트리 뒤집기 (문제 ID: QUADTREE, 난이도: 하)
3. 풀이: 쿼드 트리 뒤집기
4. 문제: 울타리 잘라내기 (문제 ID: FENCE, 난이도: 중)
5. 풀이: 울타리 잘라내기
6. 팬미팅 (문제 ID: FANMEETING, 난이도: 상)
7. 풀이: 팬미팅
1. 도입
📍
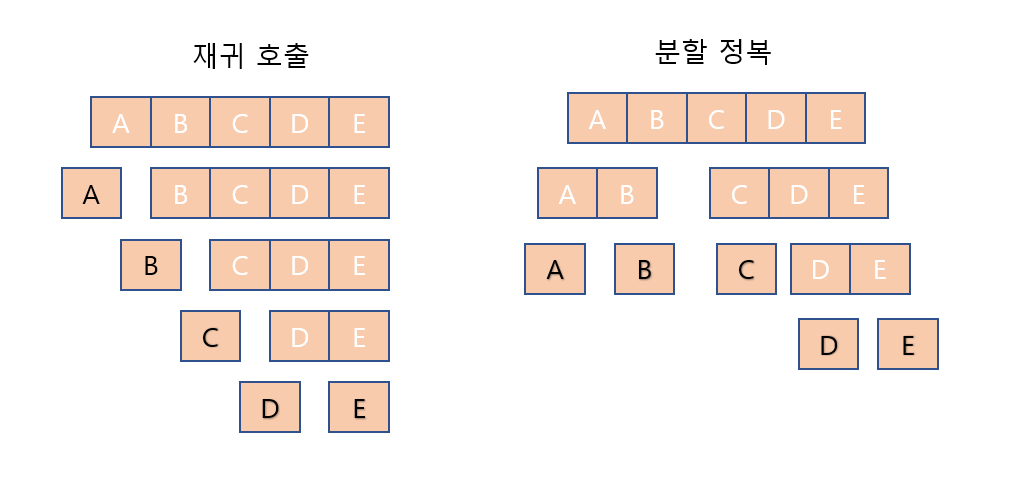
[ 분할 정복과 재귀 호출의 차이점 ]
분할 정복 : 문제를 거의 같은 크기의 부분 문제로 나눔
재귀 호출 : 문제를 한 조각 과 나머지 전체로 나눔
1️⃣ 분할 정복을 사용하는 알고리즘이 가지고 있는 3가지 특징
- Divide : 문제를 더 작은 문제로 분할하는 과정
- Merge : 각 문제에 대해 구한 답을 원래 문제에 대한 답으로 병합하는 과정
- Base case : 더 이상 답을 분할하지 않고 곧장 풀 수 있는 매우 작은 문제
2️⃣ 분할 정복을 적용하기 위한 문제의 특성
- 문제를 둘 이상의 부분 문제로 나누는 자연스러운 방법이 있어야 한다.
- 부분 문제의 답을 조합해 원래 문제의 답을 계산하는 효율적인 방법이 있어야 한다.
3️⃣ 분할 정복의 장점
- 많은 경우 같은 작업을 더 빠르게 처리해준다.
예) 수열의 빠른 합과 행렬의 빠른 제곱
// 코드 6.1 1부터 n까지의 합을 계산하는 재귀 함수
// 필수 조건: n >= 1
// 결과: 1부터 n까지의 합을 반환한다.
int recursiveSum(int n) {
if (n == 1) return 1; // 기저 사례: n = 1일 때
return n + recursiveSum(n - 1);
}분할 정복을 이용해 fastSum() 함수로 만들면, 1부터 n까지의 합을 n개의 조각으로 나눈 뒤, 반으로 나누어 n/2개의 조각들로 만들어진 부분 문제 두 개를 만들 수 있다.
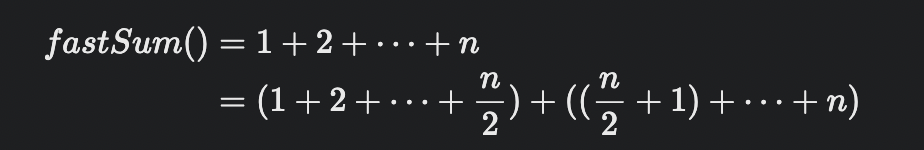
(n은 짝수)
첫 번째 부분 문제는 fastSum(n/2)로 표현할 수 있지만, 두 번째 부분 문제는 fastSum(x)를 포함하는 형태로 바꿔야 한다.
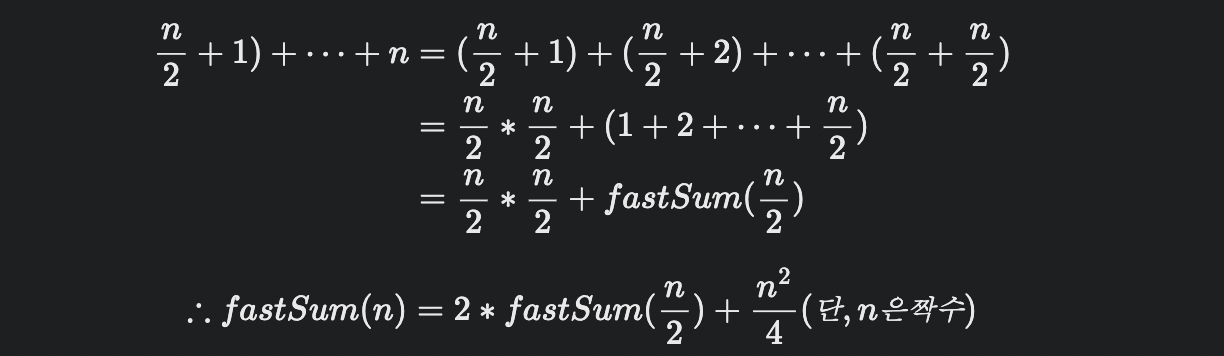
n이 홀수인 경우를 처리하기 위해서는 짝수인 n-1까지의 합을 재귀 호출하고 n을 더하면 된다.
// 코드 7.1 1부터 n까지의 합을 구하는 분할 정복 알고리즘
// 필수 조건: n은 자연수
// 1부터 n까지의 합을 반환한다
int fastSum(int n) {
// 기저 사례
if (n == 1) return 1;
return (n % 2 == 1) ? fastSum(n - 1) + n
: 2 * fastSum(n / 2) + (n / 2) * (n / 2);
}⏳ 시간 복잡도 분석
두 함수 모두 내부에 반복문이 없으므로, 종료하는 데 걸리는 시간은 함수가 호출되는 횟수에 비례한다.
recursiveSum()의 경우 n번의 함수 호출이 필요하다는 것을 알 수 있다.
fastSum()의 경우 호출될 때마다 최소한 두 번에 한 번 꼴로 n이 절반으로 줄어든다.
아래는 fastSum(11)을 실행할 때 재귀 호출의 입력이 어떻게 변화하는지를 이진수 표현으로 보여준다.

- fastSum()의 총 호출 횟수 = n의 이진수 표현의 자릿수 + 첫 자리를 제외하고 나타나는 1의 개수
두 값의 상한은 모두 이므로 이 알고리즘의 실행 시간은 이다.
행렬의 거듭제곱
가장 단순한 행렬의 거듭제곱 A^m (A는 nn 크기 행렬)
가장 단순한 행렬의 곱셈 알고리즘은 O(N^3)의 시간이 든다.
거듭제곱 A^(m)을 구하기 위해서는 O(N^3 m)의 시간이 걸린다.
❗️
분할 정복 알고리즘 : A^(m/2) + A^(m/2)
// 코드 7.2 행렬의 거듭제곱을 구하는 분할 정복 알고리즘
// 정방행렬을 표현하는 SquareMatrix 클래스
class SquareMatrix;
// n*n 크기의 항등 행렬(identity matrix)을 반환하는 함수
SquareMatrix identity(int n);
// A^m을 반환한다
SquareMatrix pow(const SquareMatrix& A, int m) {
// 기저 사례: A^0 = I
if (m == 0) return identity(A.size());
if (m % 2 > 0) return pow(A, m - 1) * A;
SquareMatrix half = pow(A, m / 2);
// A^m = (A^(m/2))^2
return half * half;
}
나누어 떨어지지 않을 때의 분할과 시간 복잡도
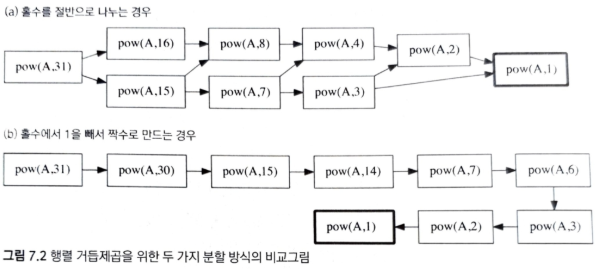
A^(m)을 찾기 위해서 계산해야 할 부분 문제의 수가 늘어나기 때문에 m이 홀수일 때 절반으로 바로 나누는 방식이 알고리즘을 더 느리게 만든다.
예) 병합 정렬과 퀵 정렬
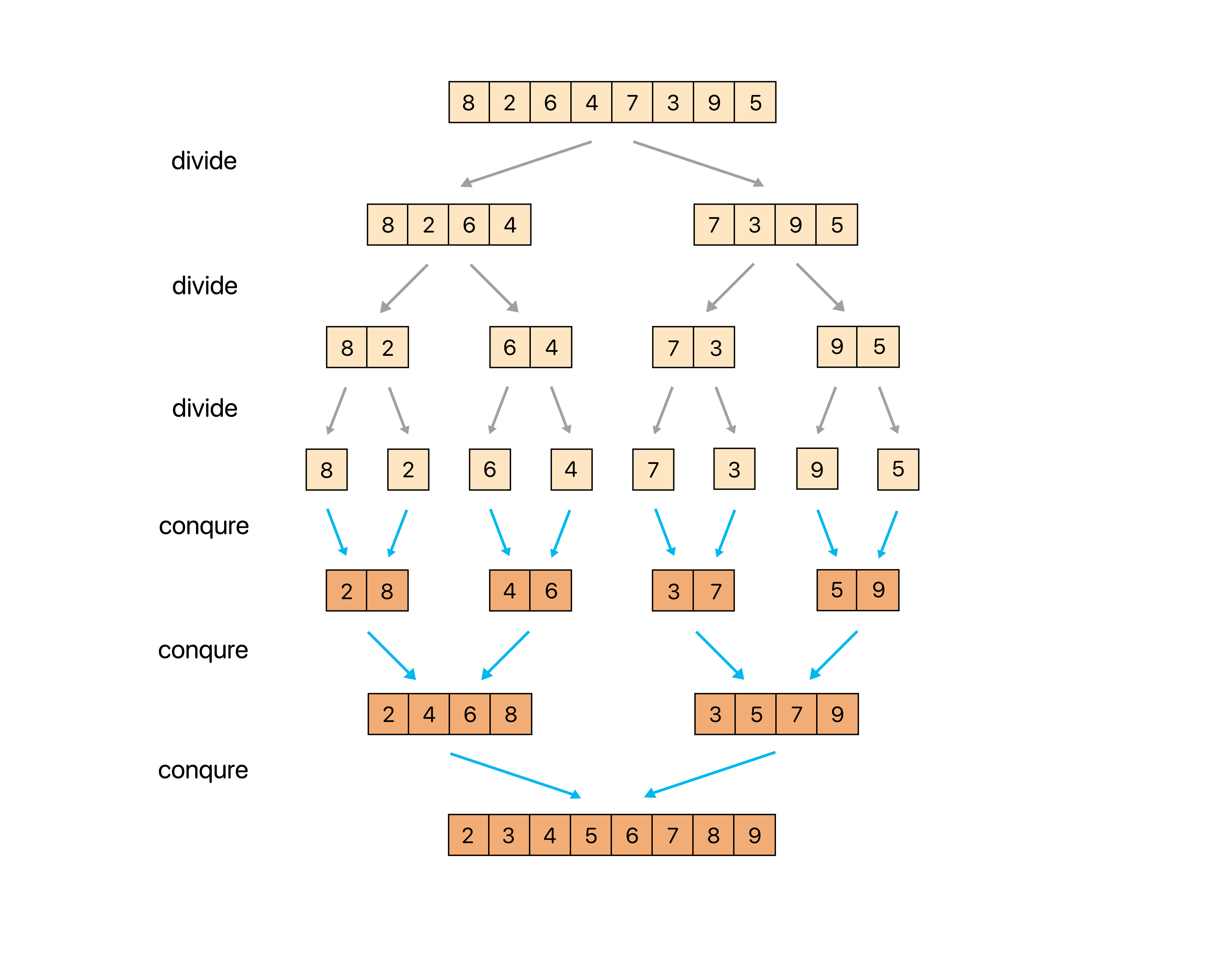
병합 정렬
수열을 가운데에서 쪼개 비슷한 크기의 수열 두 개로 만든 뒤 이들을 재귀 호출을 이용해 각각 정렬한다. 그 후 정렬된 배열을 하나로 합침으로써 정렬된 전체 수열을 얻는다.
퀵 정렬
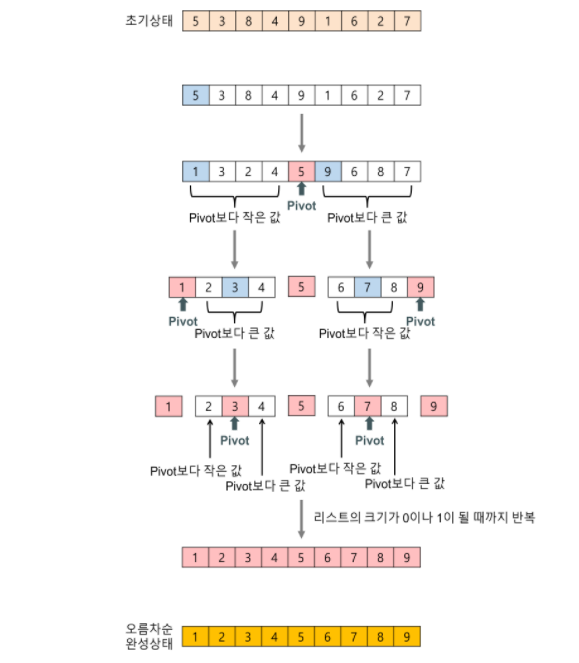
배열을 단순하게 가운데서 쪼개는 대신, 병합 과정이 필요 없도록 한쪽의 배열에 포함된 수가 다른 쪽 배열의 수보다 항상 작도록 배열을 분할한다.
파티션 : 배열에 있는 수 중 임의의 '기준 수 (pivot)'을 지정한 후 기준보다 작거나 같은 숫자를 왼쪽, 더 큰 숫자를 오른쪽으로 보내는 과정
⏳ 시간 복잡도 분석
병합 정렬
수열의 각 항의 길이가 1이 될 때까지 나누는 분할 과정 O(lgn)과 병합 과정 O(n)이 항상 일정하다.
퀵 정렬
- 평균 :
- 최악 :
대부분 부분 문제로 나누는 파티션 과정에서 시간이 소요된다.
파티션에는 주어진 수열의 길이에 비례하는 시간이 걸리므로, 병합 정렬의 병합 과정 O(n)과 같다.
문제는 기준 값인 Pivot에 의해 분할도니 부분 문제가 비슷한 크기로 나누어진다는 보장이 불가능하다.
예) 카라츠바의 빠른 곱셈 알고리즘
수백 자리, 수만 자리가 되는 큰 숫자들을 다룰 때 주로 사용한다.
- 두 정수의 곱을 구하는 함수
// 코드 7.3 두 큰 수를 곱하는 O(n^2) 시간 알고리즘
// num[]의 자릿수 올림을 처리한다
void normalize(vector<int>& num) {
num.push_back(0);
// 자릿수 올림을 처리한다
for (int i = 0; i < num.size(); i++) {
if (num[i] < 0) {
int borrow = (abs(num[i]) + 9) / 10;
num[i + 1] -= borrow;
num[i] += borrow * 10;
} else {
num[i + 1] += num[i] / 10;
num[i] %= 10;
}
}
while (num.size() > 1 && num.back() == 0) num.pop_back();
}
// 두 긴 자연수의 곱을 반환한다
// 각 배열에는 각 수의 자릿수가 1의 자리에서부터 시작해 저장되어 있다
// 예 : multiply({3, 2, 1}, {6, 5, 4}) = 123 * 456 = 56088 = {8, 8, 0, 6, 5}
vector<int> multiply(const vector<int>& a, const vector<int>& b) {
vector<int> c(a.size() + b.size() + 1, 0);
for (int i = 0; i < a.size(); i++)
for (int j = 0; j < b.size(); j++)
c[i + j] += a[i] * b[j];
normalize(c);
return c;
}카라츠바 알고리즘
분할한 부분 문제의 답에서 원래 문제의 답을 병합해내는 부분을 개선함으로써 알고리즘의 성능을 향상시킨 예이다.
스트라센의 행렬 곱셈 알고리즘 또한 이와 비슷한 기법을 사용한다.
두 수를 각각 절반으로 쪼갠다.
a,b가 각각 256자리 수라면,
이때, 의 네 개의 조각을 이용해 표현할 수 있다.
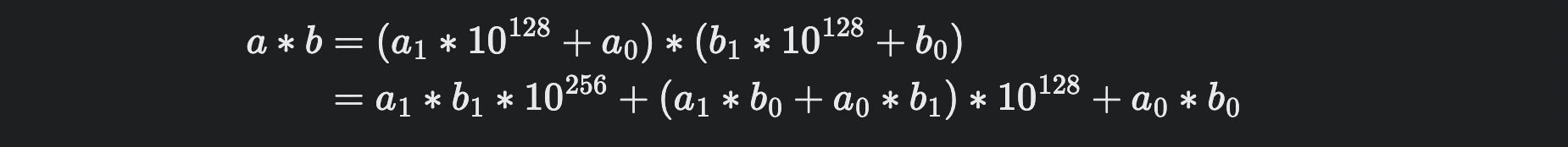
카라츠바는 를 표현했을 때 네 번 대신 세 번의 곱셈으로만 이 값을 계산할 수 있게 만들었다.
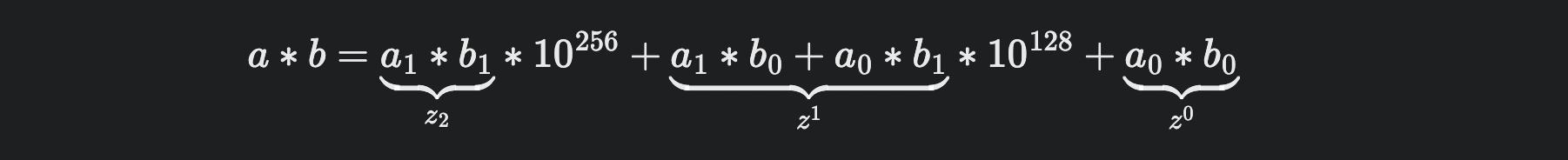
와 를 각각 한 번의 곱셈으로 구한다. 그리고 아래 식을 이용한다.
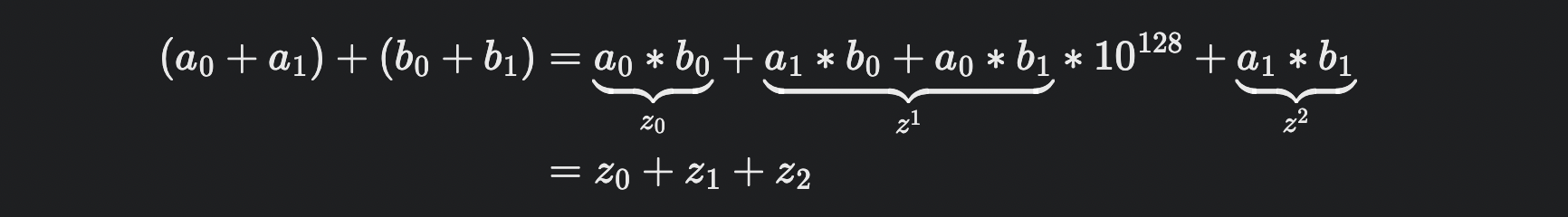
위 식의 결과에서 와 를 빼서 을 구할 수 있다.
위의 세 결과를 적절히 조합하면 두 수의 답을 구해낼 수 있으며 최종 구현은 아래의 코드와 같다.
/ 코드 7.4 카라츠바의 빠른 정수 곱셈 알고리즘
// a += b * (10^k)를 구현한다
void addTo(vector<int>& a, const vector<int>& b, int k) {
int length = b.size();
a.resize(max(a.size() + 1, b.size() + k));
for (int i = 0; i < length; i++)
a[i + k] += b[i];
normalize(a); // 정규화
}
// a -= b; 를 구현한다. a >= b를 가정한다
void subFrom(vector<int>& a, const vector<int>& b) {
int length = b.size();
a.resize(max(a.size() + 1, b.size()) + 1);
for (int i = 0; i < length; i++)
a[i] -= b[i];
normalize(a); // normalize()가 음수를 처리하는 이유
}
// 두 긴 정수의 곱을 반환한다
vector<int> karatsuba(const vector<int>& a, const vector<int>& b) {
int an = a.size(), bn = b.size();
// a가 b보다 짧을 경우 둘을 바꾼다
if (an < bn) return karatsuba(b, a);
// 기저 사례: a나 b가 비어 있는 경우
if (an == 0 || bn == 0) return vector<int>();
// 기저 사례: a가 비교적 짧은 경우 O(n^2) 곱셈으로 변경한다
if (an <= 50) return multiply(a, b);
int half = an / 2;
// a와 b를 밑에서 half 자리와 나머지로 분리한다
vector<int> a0(a.begin(), a.begin() + half);
vector<int> a1(a.begin() + half, a.end());
vector<int> b0(b.begin(), b.begin() + min<int>(b.size(), half));
vector<int> b1(b.begin() + min<int>(b.size(), half), b.end());
// z2 = a1 * b1
vector<int> z2 = karatsuba(a1, b1);
// z0 = a0 * b0
vector<int> z0 = karatsuba(a0, b0);
// a0 = a0 + a1; b0 = b0 + b1
addTo(a0, a1, 0); addTo(b0, b1, 0);
// z1 = (a0 * b0) - z0 - z2;
vector<int> z1 = karatsuba(a0, b0);
subFrom(z1, z0);
subFrom(z1, z2);
// ret = z0 + z1 * 10^half + z2 * 10^(half*2)
vector<int> ret;
addTo(ret, z0, 0); addTo(ret, z1, half); addTo(ret, z2, half + half);
return ret;
}⏳ 시간 복잡도 분석
곱셈이 시간복잡도를 지배하며, 최종 시간 복잡도는 가 된다.
입력의 크기가 작을 때는 보다 느린 경우가 많으므로 유의해야 한다.
2. 문제: 쿼드 트리 뒤집기 (문제 ID: QUADTREE, 난이도: 하)
문제 링크 : https://algospot.com/judge/problem/read/QUADTREE
3. 풀이: 쿼드 트리 뒤집기
[ 두 가지 접근 방법 ]
- 큰 입력에 대해서도 동작하는 효율적인 알고리즘을 처음부터 새로 만들기
- 작은 입력에 대해서만 동작하는 단순한 알고리즘으로부터 시작해서 최적화 해 나가기
쿼드 트리 압축 풀기
쿼드 트리가 재귀적으로 정의되어 있기 때문에 쿼드 트리를 재귀 호출로 구현하는 것이 가장 좋다.
아래는 문자열 x의 압축을 해제해서 N*N크기의 배열에 저장하는 함수 decompress()이다.
기저 사례 : x의 첫 글자가 w,b인 경우
첫 글자가 x인 경우 : s의 나머지 부분을 넷으로 쪼개 재귀 호출한다.
char decompressed[MAX_SIZE][MAX_SIZE];
void decompress(string::iterator& it, int y, int x, int size);압축 문자열 분할하기
각 부분의 길이가 일정하지 않은 경우, s의 나머지 부분을 넷으로 쪼개기 어렵다.
- 주어진 위치에서 시작하는 압축 결과의 길이를 반환하는 함수 gerChunkLength()를 만든다,
하지만, 비슷한 일을 하는 두 개의 함수를 작성하게 된다.
이때는 s를 미리 쪼개는 것이 아니라 decompress() 함수에서 '필요한 만큼 가져다 쓰도록' 한다.
STL의 문자열에서 지원하는 반복자를 재귀호출에 전달한다.
이떄 반복자가 참조명으로 전달되기 때문에 재귀 호출 내부에서 반복자를 옮기면 밖에서도 적용된다.
// 코드 7.5 쿼드 트리 압축을 해제하는 재귀 호출 알고리즘
char decompressed[MAX_SIZE][MAX_SIZE];
void decompress(string::iterator& it, int y, int x, int size) {
// 한 글자를 검사할 때마다 반복자를 한 칸 앞으로 옮긴다
char head = *(it++);
// 기저 사례: 첫 글자가 b 또는 w인 경우
if (head == 'b' || head == 'w') {
for (int dy = 0; dy < size; dy++)
for (int dx = 0; dx < size; dx++)
decompressed[y + dy][x + dx] = head;
} else {
int half = size / 2;
// 네 부분을 각각 순서대로 압축 해제한다
decompress(it, y, x, half);
decompress(it, y, x + half, half);
decompress(it, y + half, x, half);
decompress(it, y + half, x + half, half);
}
}압출 다 풀지 않고 뒤집기
압축 결과를 다 메모리에 저장하지 않고 결과 이미지를 뒤집은 결과를 곧장 생성하는 코드를 작성한다.
- 전체가 검은 색이나 흰 색인 그림을 뒤집은 결과는 원래 그림과 똑같다.
- 전체가 한 가지 색이 아닌 경우에는 재귀 호출을 이용해 네 부분을 각각 상하로 뒤집은 결과를 얻은 뒤, 이들을 병합해 답을 구한다.
// 코드 7.5 쿼드 트리 압축을 해제하는 재귀 호출 알고리즘
char decompressed[MAX_SIZE][MAX_SIZE];
void decompress(string::iterator& it, int y, int x, int size) {
// 한 글자를 검사할 때마다 반복자를 한 칸 앞으로 옮긴다
char head = *(it++);
// 기저 사례: 첫 글자가 b 또는 w인 경우
if (head == 'b' || head == 'w') {
for (int dy = 0; dy < size; dy++)
for (int dx = 0; dx < size; dx++)
decompressed[y + dy][x + dx] = head;
} else {
int half = size / 2;
// 네 부분을 각각 순서대로 압축 해제한다
decompress(it, y, x, half);
decompress(it, y, x + half, half);
decompress(it, y + half, x, half);
decompress(it, y + half, x + half, half);
}
}4. 문제: 울타리 잘라내기 (문제 ID: FENCE, 난이도: 중)
문제 링크 : https://algospot.com/judge/problem/read/FENCE
5. 풀이: 울타리 잘라내기
무식하게 풀 수 있을까?
각 판자 높이의 배열 h[]가 주어졌을 때 l번 판자부터 r번 판자까지 잘라내서 사각형을 만들자
사각형의 넓이는 아래와 같다.

- 2중 for 문으로 가능한 모든 l과 r을 순회하며 값을 계산한다.
하지만, 이 문제에서 입력의 최대 크기는 20,000이므로 이 걸리는 이 알고리즘으로 해결하기란 사실상 불가능하다.
// 코드 7.7 울타리 잘라내기 문제를 해결하는 O(n^2) 알고리즘
// 판자의 높이를 담은 배열 h[]가 주어질 때 사각형의 최대 너비를 반환한다
int bruteForce(const vector<int>& h) {
int ret = 0;
int N = h.size();
// 가능한 모든 left, right 조합을 순회한다
for (int 수비 = 0; 수비 < N; 수비++) {
int minHeight = h[수비];
for (int 희진 = 수비; 희진 < N; 희진++) {
minHeight = min(minHeight, h[희진]);
ret = max(ret, (희진 - 수비 + 1) * minHeight);
}
}
return ret;
}분할 정복 알고리즘의 설계
- 문제를 어떻게 분할해야 할 지 결정해야 한다.
- n 개의 판자를 절반으로 나눠 두 개의 부분 문제를 만들자
그러면, 우리가 찾는 최대 직사각형은 다음 세 가지 중 하나에 속한다.
- 가장 큰 직사각형을 왼쪽 부분 문제에서만 잘라낼 수 있다.
- 가장 큰 직사각형을 오른쪽 부분 문제에서만 잘라낼 수 있다.
- 가장 큰 직사각형은 왼쪽 부분 문제와 오른쪽 부분 문제에 걸쳐 있다.
반으로 나눈 부분 문제는 재귀호출을 하여 해결한다.
가장 큰 사각형의 넓이를 찾고 있기 때문에 이 중 더 큰 것을 항상 선택한다.
그 후, 세 번째 경우의 답만 빠르게 구하면, 분할 정복 알고리즘은 완성이다.
양쪽 부분 문제에 걸친 경우의 답
여러 경우의 수 중 더 높은 판자를 포함하게끔 확장해야 한다.
max(부분문제1(), 부분문제2())로 재귀를 호출하여 문제를 해결하고, 최종적으로 두 부분 모두 걸치는 직사각형을 탐색하면 된다.
// 코드 7.8 울타리 잘라내기 문제를 해결하는 분할 정복 알고리즘
// 각 판자의 높이를 저장하는 배열
vector<int> h;
// h[left..right] 구간에서 찾아낼 수 있는 가장 큰 사각형의 넓이를 반환한다
int solve(int left, int right) {
// 기저 사례: 판자가 하나밖에 없는 경우
if (left == right) return h[left];
// [left, mid], [mid + 1, right]의 두 구간으로 문제를 분할한다
int mid = (left + right) / 2;
// 분할한 문제를 각개격파
int ret = max(solve(left, mid), solve(mid + 1, right));
// 부분 문제 3: 두 부분에 모두 걸치는 사각형 중 가장 큰 것을 찾는다
int lo = mid, hi = mid + 1;
int height = min(h[lo], h[hi]);
// [mid, mid + 1]만 포함하는 너비 2인 사각형을 고려한다
ret = max(ret, height * 2);
// 사각형이 입력 전체를 덮을 때까지 확장해 나간다
while (left < lo || hi < right) {
// 항상 높이가 더 높은 쪽으로 확장한다
if (hi < right && (lo == left || h[lo - 1] < h[hi + 1])) {
++hi;
height = min(height, h[hi]);
} else {
--lo;
height = min(height, h[lo]);
}
// 확장한 후 사각형의 넓이
ret = max(ret, height * (hi - lo + 1));
}
return ret;
}정당성 증명
귀류법을 이용해 양쪽 부분 문제에 걸쳐 있는 직사각형을 찾을 때, 각 단계마다 더 높은 판자를 택하는 것이 항상 옳음을 보여야한다.
귀류법
어떤 주장에 대해 그 함의하는 내용을 따라가다보면 이치에 닿지 않는 내용 또는 결론에 이르게 된다는 것을 보여서 그 주장이 잘못된 것임을 보이는 것
어떤 사각형 R이 우리가 위의 과정을 통해 찾은 최대 직사각형보다 더 크다고 가정해보자.
우리가 고려한 사각형들 중 R과 넓이가 같은 사각형이 반드시 하나가 존재한다. 이를 RR이라고 하자.
너비가 같으므로 R이 더 넓기 위해서는 높이가 반드시 RR보다 높아야 한다.
R과 RR은 둘 다 부분 문제 경게에 있는 두 개의 판자를 포함하므로 항상 겹치는 부분이 존재한다.
이때 RR의 높이를 결정하는 가장 낮은 판자 A를 보면, R이 RR보다 높으니, R에 포함된 모든 판자들은 당연히 A보다 높아야 한다.
우리의 알고리즘은 현재 사각형의 양쪽 끝에 있는 두 판자 중 항상 더 높은 것을 선택하므로, A보다 낮거나 높이가 같은 판자를 만나야만 A를 선택한다.
그런데, RR을 만드는 과정에서 만나는 반대쪽 판자들은 모두 R에 속해 있으므로 A보다 높다.
따라서 A를 선택하는 경우가 있을 수 없으며, R이 RR보다 높다는 가정은 모순이 된다.
시간 복잡도 분석
문제를 2개로 나누고, 너비가 2인 사각형에서 너비가 n인 사각형까지를 하나씩 검사하므로 분할 ln(n)과 탐색 n의 시간을 곱하면 최종 시간복잡도는 이다.
선형 시간 알고리즘
사실, 이 문제는 스위핑 기법과 스택을 결합한 선형 시간 알고리즘으로 풀 수도 있다.
상호 배타적 집합을 사용하여도 풀 수 있는데, 시간 복잡도는 모두 으로 동일하다.
6. 팬미팅 (문제 ID: FANMEETING, 난이도: 상)
문제 링크 : https://algospot.com/judge/problem/read/FANMEETING
7. 풀이: 팬미팅
단순한 방법은 문제에 나와 있는 과정대로 팬미팅 과정을 하나하나 구현하는 것이다.
팬의 수를 N, 멤버의 수를 M이라고 할 때 이 방법은 대략 의 시간 복잡도를 가진다.
곱셈으로의 변형
두 큰 수의 곱셈으로 이 문제를 바꿔보자.
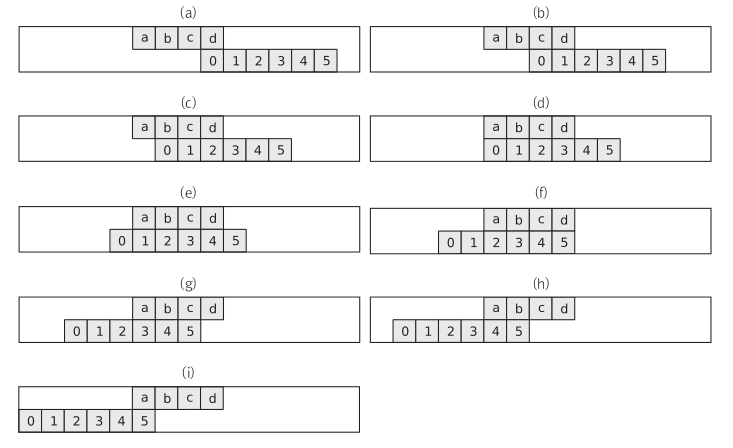
남자는 1, 여자는 0으로 값을 치환한다.
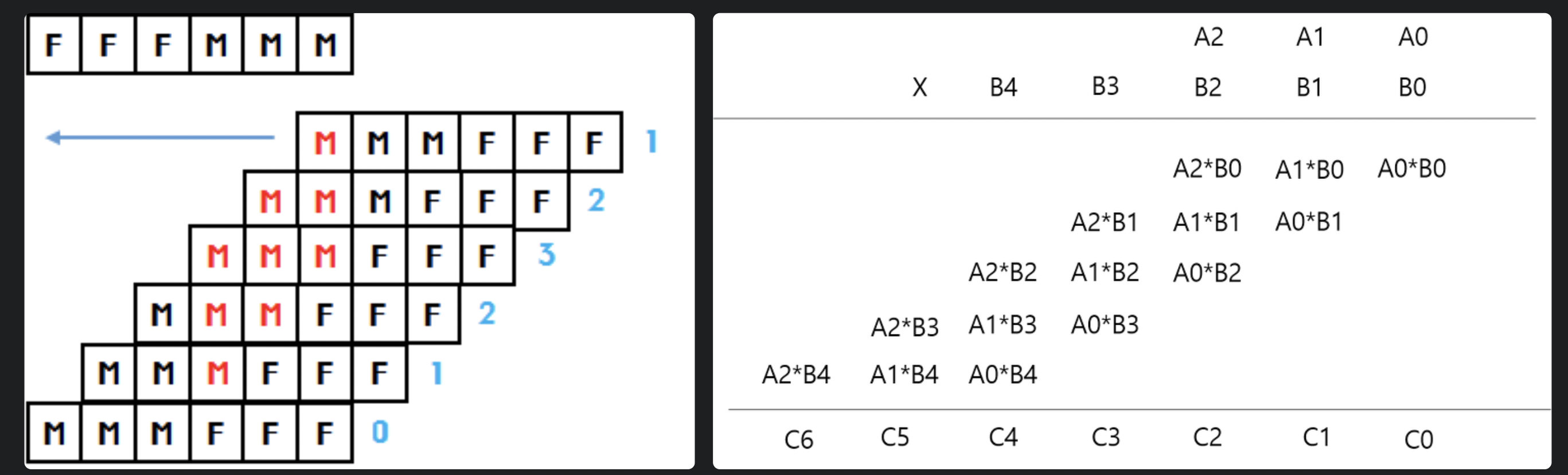
연산을 위해 A의 원소를 뒤집자.
위와 같이 곱셈으로 변형해 문제를 풀 수 있다.
카리츠바 알고리즘을 이용한 구현

N, M이 최대 20만이므로 이전에 배웠던 카라츠바 알고리즘을 적용할 수 있다.
이 알고리즘의 수행 시간은 두 수의 곱셈에 좌우되므로 이다.
// 카라츠바의 빠른 정수 곱셈 알고리즘을 이용해 팬미팅 문제를 해결하는 함수
vector<int> karatsuba(vector<int>& a, vector<int>& b);
int hugs(const string& members, const string& fans) {
int N = members.size(), M = fans.size();
vector<int> A(N), B(M);
for (int i = 0; i < N; ++i) A[i] = (members[i] == 'M');
for (int i = 0; i < M; ++i) B[M - i - 1] = (fans[i] == 'M');
// 카라츠바 알고리즘에서 자리 올림은 생략한다
vector<int> C = karatsuba(A, B);
int allHugs = 0;
for (int i = N - 1; i < M; ++i)
if (C[i] == 0)
++allHugs;
return allHugs;
}