
다중 선형 회귀
우리는 앞에서 입력 변수가 1개인 경우만 살펴봤습니다. 여러 입력변수로 하는 선형 회귀를 다중 선형 회귀라 합니다.
다중 선형 회귀는 시각적으로 표현하기 힘듭니다. 하지만 시각화만 못할 뿐이지 기본 개념은 이전과 같습니다.
다중 선형 회귀 표현법
입력변수를 다른 말로 속성(feature)이라 합니다.

다중 선형 회귀 가설 함수
가설함수는 입력 변수들로 목표 변수를 예측해줍니다. 다중 선형 회귀의 가설 함수는 다음과 같습니다.
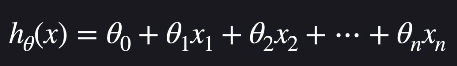
항이 많아졌을 뿐, 이 함수도 일차 함수입니다. 다중 선형 회귀에서도 목적은 θ값들을 조금씩 조율하면서 학습데이터에 가장 잘 맞는 θ값들을 찾는 것입니다.
벡터표현을 통해 다음과 같이 가설함수를 간단하게 나타낼 수 있습니다.
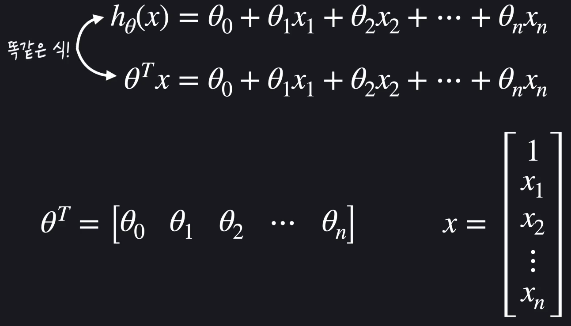
다중 선형 회귀 경사 하강법
가설함수의 성능을 평가하는 손실함수는 선형회귀에서 다음과 같습니다.
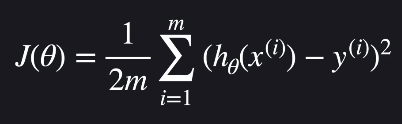
손실 함수가 작을수록 가설함수가 데이터에 잘 맞다는 것입니다.
경사 하강법은 손실을 가장 빨리 줄이는 방향으로 θ값들을 바꿔주는 방법입니다.
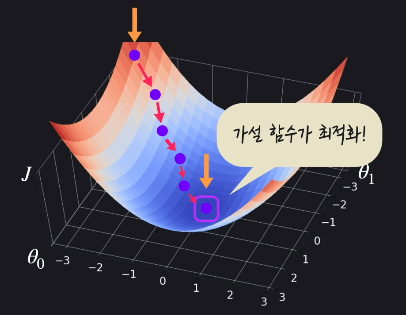
다중 선형 회귀에서 시각적으로 표현하는건 어렵지만, 수학적으로 보면 거의 같습니다. 단지, 업데이트할 θ값이 많아지는 것입니다.
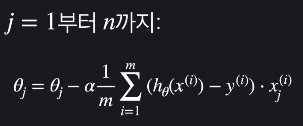
다중 선형 회귀 구현하기 쉽게 표현하기
입력 변수 데이터를 하나의 행렬 X로 묶어서 표현한걸 설계행렬(Design Matrix)라고 합니다.
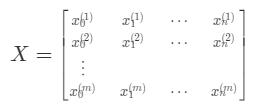
이때, 통일성을 위해 가상의 0번쨰 속성 x0를 만들고, 값을 항상 1로 설정해줍니다.
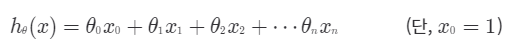
θ도 두개이상이면 하나의 벡터로 표현합니다.

이를 통해 경사하강법 공식을 간단한 행렬식으로 표현할 수 있게 됩니다.
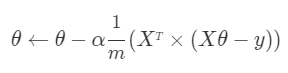
정규 방정식
조금씩 찾아가는게 아니라 미분을 통해 한번에 극소점으로 갈 수 있습니다.

이러한 방식을 정규 방정식(Normal Equation)이라 합니다.
중간 과정을 통해 다음과 같은 식으로 기울기가 0이 되는 θ를 구할 수 있습니다.

경사 하강법 vs 정규 방정식
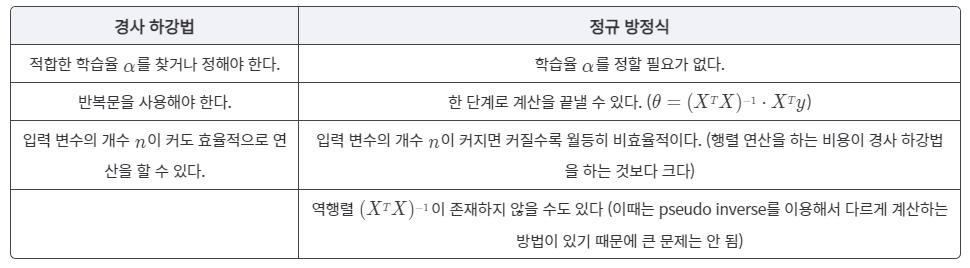
입력변수(속성)의 수가 엄청 많을 때(1000개 이상)는 경사 하강법을, 아닐때는 정규 방정식을 사용합니다.
Convex 함수
함수가 생긴 모양에 따라 경사 하강법과 정규 방정식을 통해서 구한 극소 지점이 손실 함수 전체에서 최소 지점이라고 확실하게 얘기할 수 없습니다.
하지만, 다음과 같은 convex 함수에서는 항상 경사 하강법이나 정규 방정식을 이용해서 최소점을 구할 수 있습니다.
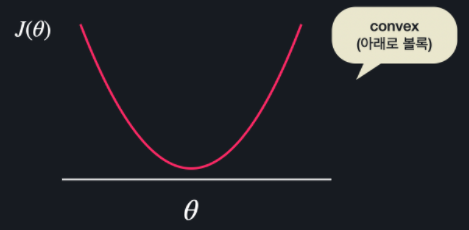
선형 회귀 손실 함수로 사용하는 MSE는 항상 convex 함수입니다.
scikit-learn 데이터 준비
from sklearn.datasets import load_boston
import pandas as pd
boston_dataset = load_boston()
print(boston_dataset.DESCR)
print(boston_dataset.feature_names)
print(boston_dataset.data)
X = pd.DataFrame(boston_dataset.data, columns = boston_dataset.feature_names)
print(X)
y = pd.DataFrame(boston_dataset.target,columns=['MEDV'])
print(y)scikit-learn으로 다중 선형 회귀 쉽게 하기
위 데이터 준비에 이어서
from sklearn.model_selection import train_test_split #train, test 나누기 위해
from sklearn.linear_model import LinearRegression #선형회귀하기 위해
from sklearn.metrics import mean_squared_error #평균제곱오차 구하기 위해
# train_test_split를 사용해서 주어진 데이터를 학습, 테스트 데이터로 나눈다
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state=5)
linear_regression_model = LinearRegression() #선형 회귀 모델을 가지고 오고
linear_regression_model.fit(X_train, y_train) #학습 데이터를 이용해서 모델을 학습 시킨다
inear_regression_model.coef_ #θ1~ 값
inear_regression_model.intercept_ #θ0값
y_test_predict = linear_regression_model.predict(X_test) #학습시킨 모델로 예측
#평균 제곱 오차의 루트를 통해서 테스트 데이터에서의 모델 성능 판단
mse = mean_squared_error(y_test, y_test_predict)
mse ** 0.5
scikit-learn으로 당뇨 수치 예측하기
# 필요한 라이브러리 import
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import pandas as pd
# 당뇨병 데이터 갖고 오기
diabetes_dataset = datasets.load_diabetes()
# 입력 변수를 사용하기 편하게 pandas dataframe으로 변환
X = pd.DataFrame(diabetes_dataset.data, columns=diabetes_dataset.feature_names)
# 목표 변수를 사용하기 편하게 pandas dataframe으로 변환
y = pd.DataFrame(diabetes_dataset.target, columns=['diabetes'])
# train_test_split를 사용해서 주어진 데이터를 학습, 테스트 데이터로 나눈다
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state=5)
linear_regression_model = LinearRegression() # 선형 회귀 모델을 가지고 오고
linear_regression_model.fit(X_train, y_train) # 학습 데이터를 이용해서 모델을 학습 시킨다
y_test_predict = linear_regression_model.predict(X_test) # 학습시킨 모델로 예측
# 평균 제곱 오차의 루트를 통해서 테스트 데이터에서의 모델 성능 판단
mse = mean_squared_error(y_test, y_test_predict)
mse ** 0.5