[알고리즘] 그래프

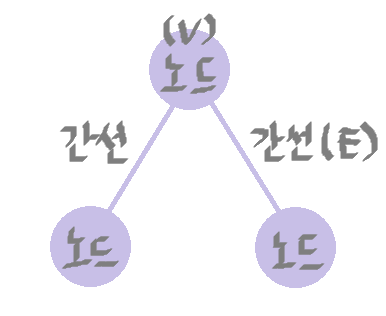
그래프(Graph)

정점/노드 사이에 연결된 간선(Edge)의 정보를 가진 자료구조.
트리, 힙도 그래프에 속한다.

구현방법 1) 인접행렬(Adjacency Matrix)

1) 인접 행렬 : 그래프 연결 관계를 2차원 배열로 나타냄.
ex. i-j를 잇는 간선이 존재하면 adj[i][j] = 1, 없으면 0
혹은 간선 거리나 비용 표시

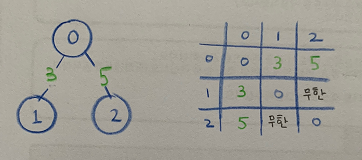
INF = 999999999  # 무한의 비용 선언
# 2차원 리스트를 이용해 인접 행렬 표현
graph = [
    [0, 3, 5],
    [3, 0, INF],
    [5, INF, 0]
]

간선 정보를 저장하기 위해 O(V^2)만큼의 메모리 공간이 필요한 반면, 간선 비용은 O(1)로 연결 정보를 즉시 알 수 있다는 장점이 있다.
'플로이드 워셜 알고리즘'에서 사용.
즉, 노드 개수가 적은 경우에 사용하면 좋다.

구현방법 2) 인접 리스트(Adjacency List)

2) 인접 리스트 : 모든 노드에 연결된 노드에 대한 정보를 차례로 연결해 저장.
ex. 노드i와 연결된 노드 adj[i] = j

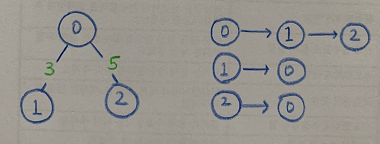
# 행이 3개인 2차원 리스트로 인접 리스트 표현
graph = [[] for _ in range(3)]

# 노드 0에 연결된 정보 저장 (노드, 거리)
graph[0].append((1, 3))
graph[0].append((2, 5))
# 노드 1에 연결된 정보 저장 (노드, 거리)
graph[1].append((0, 3))
# 노드 2에 연결된 정보 저장 (노드, 거리)
graph[2].append((0, 5))

간선의 개수인 O(E)만큼 메모리 공간이 필요하다.
간선 비용은 O(V).
'다익스트라 최단 경로 알고리즘'에서 사용.
노드와 간선이 둘 다 많을 때 사용하면 좋다.

• 리스트로 구현

graph = [[] for _ in range(V)]  // 노드가 1부터 시작하면 V+1
for _ in range(E):
  a, b = map(int, input().split())
  graph[a].append(b)
  graph[b].append(a)           // 양방향일 경우 추가

• 딕셔너리로 구현

from collections import defaultdict

graph = defaultdict(list)
for _ in range(E):
	a, b = map(int, input().split())
	graph[a].append(b)
        graph[b].append(a)    // 양방향일 경우 추가